什麼是邏輯回歸？ 了解何時使用它

生活充滿了艱難的二元選擇。

我應該吃那片披薩嗎？ 我應該帶傘還是不帶傘？

雖然有些決定可以通過權衡利弊來做出正確的決定——例如，最好不要吃一片比薩餅，因為它含有額外的卡路里——但有些決定可能並不那麼容易。

例如，您永遠無法完全確定某一天是否會下雨。 所以要不要帶雨傘是一個艱難的決定。

為了做出正確的選擇，需要預測能力。 這種能力非常有利可圖，並且在現實世界中有許多應用，尤其是在計算機中。 計算機喜歡二元決策。 畢竟，他們說的是二進制代碼。

機器學習  算法，更準確地說是邏輯回歸算法，可以通過查看歷史數據點來幫助預測事件的可能性。 例如，它可以預測個人是否會贏得選舉或今天是否會下雨。

如果您想知道什麼是回歸分析，它是一種預測建模技術，用於查找因變量與一個或多個自變量之間的關係。

自變量的一個例子是花在學習上的時間和花在 Instagram 上的時間。 在這種情況下，成績將是因變量。 這是因為“學習時間”和“在 Instagram 上花費的時間”都會影響成績； 一個是積極的，另一個是消極的。

邏輯回歸是一種基於一系列自變量預測二元結果的分類算法。 在上面的例子中，這意味著預測你是否會通過或失敗。 當然，邏輯回歸也可以用來解決回歸問題，但主要用於分類問題。

另一個例子是預測學生是否會被大學錄取。 為此，將考慮SAT分數、學生的平均成績和課外活動的數量等多種因素。 使用有關先前結果的歷史數據，邏輯回歸算法將學生分為“接受”或“拒絕”類別。

邏輯回歸也稱為二項邏輯回歸或二元邏輯回歸。 如果響應變量的類別超過兩類，則稱為多項邏輯回歸。 毫不奇怪，邏輯回歸是從統計學中藉用的，是機器學習和數據科學中最常見的二元分類算法之一。

邏輯回歸通過測量因變量（我們想要預測的）和一個或多個自變量（特徵）之間的關係來工作。 它通過在其基礎邏輯函數的幫助下估計概率來做到這一點。

邏輯回歸中的關鍵術語

理解術語對於正確解讀邏輯回歸的結果至關重要。 如果您不熟悉統計或機器學習，了解特定術語的含義將有助於您快速學習。

什麼是邏輯函數？

邏輯回歸以其核心使用的函數命名，邏輯函數。 統計學家最初用它來描述人口增長的特性。 Sigmoid 函數和logit 函數是邏輯函數的一些變體。 Logit 函數是標準邏輯函數的逆函數。

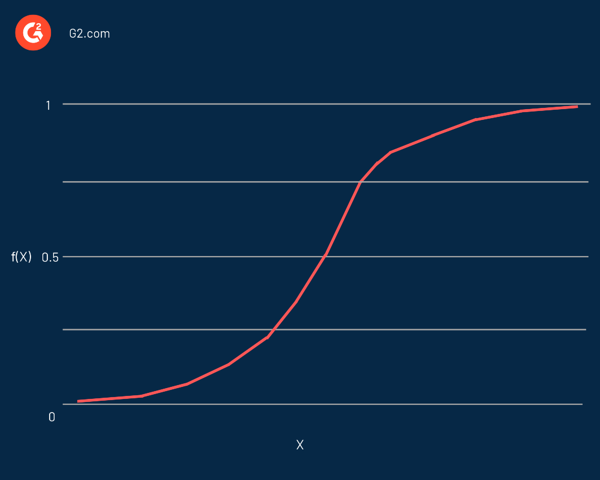
實際上，它是一條 S 形曲線，能夠取任何實數並將其映射為 0 到 1 之間的值，但絕不會精確到這些限制。 它由等式表示：

在這個等式中：

• f(X)是函數的輸出
• L是曲線的最大值
• e是自然對數的底
• k是曲線的陡度
• x是實數
• x0是 sigmoid 中點的 x 值

如果預測值是相當大的負值，則認為它接近於零。 另一方面，如果預測值是一個顯著的正值，則認為它接近一個。

邏輯回歸的表示方式類似於使用直線方程定義線性回歸的方式。 與線性回歸的一個顯著區別是輸出將是二進制值（0 或 1）而不是數值。

這是邏輯回歸方程的示例：

在這個等式中：

• y是預測值（或輸出）
• b0是偏差（或截距項）
• b1是輸入的係數
• x是預測變量（或輸入）

因變量通常遵循  伯努利分佈。 使用最大似然估計 (MLE) 、梯度下降和隨機梯度下降來估計係數的值。

與其他分類算法一樣，如  k-最近鄰，a   混淆矩陣  用於評估邏輯回歸算法的準確性。

就像評估分類器的性能一樣，了解模型為什麼以特定方式對觀察進行分類同樣重要。 換句話說，我們需要分類器的決定是可解釋的。

儘管可解釋性不容易定義，但其主要目的是人類應該知道算法為何做出特定決定。 在邏輯回歸的情況下，它可以與統計測試相結合，如  沃爾德測試  或者  似然比檢驗  為了可解釋性。

何時使用邏輯回歸

邏輯回歸用於預測分類因變量。 換句話說，它用於預測是分類的，例如是或否，真或假，0或1。邏輯回歸的預測概率或輸出可以是其中之一，沒有中間立場。

在預測變量的情況下，它們可以是以下任何類別的一部分：

• 連續數據：可以在無限範圍內測量的數據。 它可以取兩個數字之間的任何值。 例如，以磅為單位的重量或以華氏度為單位的溫度。
• 離散的名義數據：適合命名類別的數據。 一個簡單的例子是頭髮顏色：金色、黑色或棕色。
• 離散的有序數據：符合某種規模順序的數據。 一個例子是告訴你對產品或服務的滿意程度，從一到五。

邏輯回歸分析對於預測事件的可能性很有價值。 它有助於確定任何兩個類別之間的概率。

從本質上講，邏輯回歸有助於解決概率和分類問題。 換句話說，您只能期望邏輯回歸的分類和概率結果。

例如，它可用於確定某事為“真或假”的概率，也可用於在“是或否”等兩種結果之間做出決定。

邏輯回歸模型還可以幫助對提取、轉換和加載 (ETL) 操作的數據進行分類。 如果觀察數少於特徵數，則不應使用邏輯回歸。 否則，可能會導致過擬合。

線性回歸與邏輯回歸

雖然邏輯回歸預測一個或多個自變量的分類變量，   線性回歸  預測連續變量。 換句話說，邏輯回歸提供恆定輸出，而線性回歸提供連續輸出。

由於結果在線性回歸中是連續的，因此結果有無限可能的值。 但是對於邏輯回歸，可能的結果值的數量是有限的。

在線性回歸中，因變量和自變量應該是線性相關的。 在邏輯回歸的情況下，自變量應與  對數賠率  (log (p/(1-p))。

雖然使用普通最小二乘法估計線性回歸，但使用最大似然估計方法估計邏輯回歸。

邏輯回歸和線性回歸都是  監督機器學習  算法和回歸分析的兩種主要類型。 雖然邏輯回歸用於解決分類問題，但線性回歸主要用於回歸問題。

回到學習時間的例子，線性回歸和邏輯回歸可以預測不同的事情。 邏輯回歸可以幫助預測學生是否通過了考試。 相比之下，線性回歸可以預測學生的分數。

邏輯回歸假設

在使用邏輯回歸時，我們做了一些假設。 假設對於正確使用邏輯回歸進行預測和解決分類問題是不可或缺的。

邏輯回歸的類型

邏輯回歸可以根據因變量的結果數量或類別分為不同的類型。

當我們想到邏輯回歸時，我們很可能會想到二元邏輯回歸。 在本文的大部分內容中，當我們提到邏輯回歸時，我們指的是二元邏輯回歸。

以下是邏輯回歸的三種主要類型。

二元邏輯回歸

二元邏輯回歸是一種統計方法，用於預測因變量和自變量之間的關係。 在這種方法中，因變量是一個二元變量，這意味著它只能取兩個值（是或否、真或假、成功或失敗、0 或 1）。

二元邏輯回歸的一個簡單示例是確定電子郵件是否為垃圾郵件。

多項邏輯回歸

多項邏輯回歸是二元邏輯回歸的擴展。 它允許超過兩個類別的結果或因變量。

它類似於二元邏輯回歸，但可以有兩個以上的可能結果。 這意味著結果變量可以具有三個或更多可能的無序類型——沒有數量意義的類型。 例如，因變量可以表示“A 型”、“B 型”或“C 型”。

與二元邏輯回歸類似，多項邏輯回歸也使用最大似然估計來確定概率。

例如，多項邏輯回歸可以用來研究一個人的教育和職業選擇之間的關係。 在這裡，職業選擇將是由不同職業類別組成的因變量。

序數邏輯回歸

序數邏輯回歸，也稱為序數回歸，是二元邏輯回歸的另一種擴展。 它用於預測具有三個或更多可能的有序類型的因變量——具有定量意義的類型。 例如，因變量可以表示“非常不同意”、“不同意”、“同意”或“非常同意”。

它可用於確定工作績效（差、平均或優秀）和工作滿意度（不滿意、滿意或非常滿意）。

邏輯回歸的優缺點

邏輯回歸模型的許多優點和缺點都適用於線性回歸模型。 邏輯回歸模型最顯著的優勢之一是它不僅可以分類，還可以給出概率。

然而，邏輯回歸有許多缺點。 如果有一個特徵可以完美地分離兩個類，那麼這個模型就不能再訓練了。 這稱為完全分離。

這主要是因為該特徵的權重不會收斂，因為最佳權重將是無限的。 然而，在大多數情況下，完全分離可以通過定義權重的先驗概率分佈或引入權重的懲罰來解決。

當生活給你選擇時，想想邏輯回歸

許多人可能會爭辯說，與計算機不同，人類並不生活在二進制世界中。 當然，如果給你一片披薩和一個漢堡包，你可以兩口都吃，而不必只選擇一個。 但是，如果您仔細觀察它，就會發現（字面上）一切都刻有二元決定。 你可以選擇吃或不吃披薩； 沒有中間立場。

如果數據量有限，評估預測模型的性能可能會很棘手。 為此，您可以使用一種稱為交叉驗證的技術，該技術涉及將可用數據劃分為訓練集和測試集。