ロジスティック回帰とはいつ使用するかを学ぶ
公開: 2021-07-29人生は厳しい二者択一に満ちています。
あのピザを食べるべきかどうか? 傘を持っていくべきかどうか?
長所と短所を比較検討することで適切な決定を下すことができるものもありますが、たとえば、ピザには余分なカロリーが含まれているため、スライスを食べないほうがよいなど、決定がそれほど簡単ではない場合もあります。
たとえば、特定の日に雨が降るかどうかを完全に確信することはできません。 そのため、傘を持ち歩くかどうかの判断は難しいものです。
正しい選択を行うには、予測機能が必要です。 この能力は非常に有利であり、特にコンピューターでは、数多くの実世界での応用があります。 コンピューターは二者択一が大好きです。 結局のところ、彼らはバイナリ コードで話します。
機械学習 アルゴリズム、より正確にはロジスティック回帰アルゴリズムは、過去のデータ ポイントを調べることでイベントの可能性を予測するのに役立ちます。 たとえば、個人が選挙に勝つかどうか、または今日雨が降るかどうかを予測できます。
ロジスティック回帰とは
ロジスティック回帰は、以前の観測に基づいて従属変数の結果を予測するために使用される統計的手法です。 これは回帰分析の一種であり、バイナリ分類の問題を解決するために一般的に使用されるアルゴリズムです。
回帰分析とは、従属変数と 1 つ以上の独立変数との関係を見つけるために使用される予測モデリング手法の一種です。
独立変数の例としては、勉強に費やした時間と Instagram に費やした時間があります。 この場合、成績は従属変数になります。 これは、「勉強に費やした時間」と「Instagram に費やした時間」の両方が成績に影響するためです。 一方は肯定的で、もう一方は否定的です。
ロジスティック回帰は、一連の独立変数に基づいてバイナリ結果を予測する分類アルゴリズムです。 上記の例では、これはクラスに合格するか不合格になるかを予測することを意味します。 もちろん、ロジスティック回帰は回帰問題の解決にも使用できますが、主に分類問題に使用されます。
ヒント:単調なタスクを自動化し、データ主導の意思決定を行うには、機械学習ソフトウェアを使用します。
もう 1 つの例は、学生が大学に受け入れられるかどうかを予測することです。 そのために、SATスコア、学生の成績平均点、課外活動の数などの複数の要因が考慮されます。 以前の結果に関する履歴データを使用して、ロジスティック回帰アルゴリズムは学生を「受け入れる」または「拒否する」カテゴリに分類します。
ロジスティック回帰は、二項ロジスティック回帰またはバイナリ ロジスティック回帰とも呼ばれます。 応答変数のクラスが 3 つ以上ある場合は、多項ロジスティック回帰と呼ばれます。 当然のことながら、ロジスティック回帰は統計から借用されたもので、機械学習とデータ サイエンスで最も一般的な二項分類アルゴリズムの 1 つです。
知ってますか? 人工ニューラル ネットワーク (ANN) 表現は、多数のロジスティック回帰分類子を積み重ねたものと見なすことができます。
ロジスティック回帰は、従属変数 (予測したいもの) と 1 つ以上の独立変数 (特徴) の間の関係を測定することによって機能します。 これは、基礎となるロジスティック関数を使用して確率を推定することによって行われます。
ロジスティック回帰の重要な用語
用語を理解することは、ロジスティック回帰の結果を適切に解読するために重要です。 統計学や機械学習に慣れていない場合は、特定の用語の意味を知っておくと、すぐに学習できます。
- 変数:測定またはカウントできる任意の数、特性、または量。 年齢、速度、性別、収入などがその例です。
- 係数:付随する変数を掛けた数値 (通常は整数)。 たとえば、12y では、数値 12 が係数です。
- EXP: exponential の短縮形。
- 外れ値:他のデータと大きく異なるデータ ポイント。
- 推定値:パラメータの推定値を生成するアルゴリズムまたは式。
- カイ 2 乗検定: カイ 2 乗検定とも呼ばれ、データが期待どおりかどうかを確認する仮説検定方法です。
- 標準誤差:統計サンプル母集団のおおよその標準偏差。
- 正則化:トレーニング データ セットに関数を (適切に) 適合させることにより、エラーと過適合を減らすために使用される方法。
- 多重共線性: 2 つ以上の独立変数間の相互相関の発生。
- 適合度:統計モデルが一連の観測にどの程度適合しているかの説明。
- オッズ比: 2 つのイベント間の関連性の強さの尺度。
- 対数尤度関数:統計モデルの適合度を評価します。
- Hosmer–Lemeshow 検定:観測されたイベント率が予想されるイベント率と一致するかどうかを評価する検定。
ロジスティック関数とは?
ロジスティック回帰は、その中心で使用される関数であるロジスティック関数にちなんで名付けられました。 統計学者は当初、人口増加の特性を説明するためにそれを使用していました。 シグモイド関数とロジット関数は、ロジスティック関数の一部のバリエーションです。 ロジット関数は、標準のロジスティック関数の逆関数です。
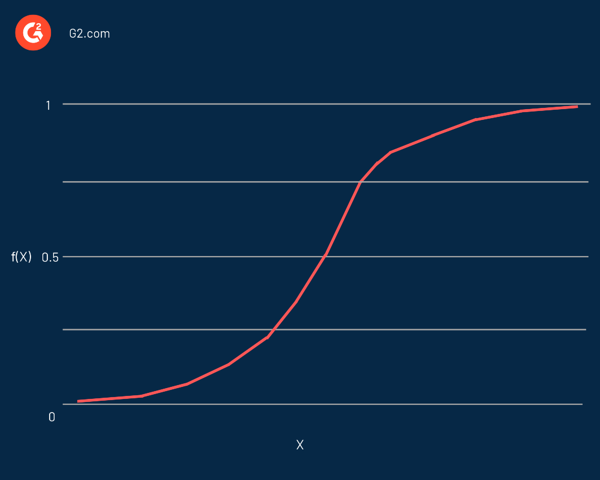
実際には、これは任意の実数を取り、それを 0 から 1 の間の値にマッピングできる S 字型の曲線ですが、正確にそれらの限界に達することは決してありません。 これは次の式で表されます。
f(x) = L / 1 + e^-k(x - x0)
この方程式では:
- f(X)は関数の出力です
- Lは曲線の最大値です
- eは自然対数の底です
- kは曲線の急峻さ
- xは実数です
- x0は、シグモイド中点の x 値です。
予測値がかなりの負の値である場合は、ゼロに近いと見なされます。 一方、予測値が有意な正の値である場合は、1 に近いと見なされます。
ロジスティック回帰は、直線の方程式を使用して線形回帰を定義する方法と同様に表されます。 線形回帰との顕著な違いは、出力が数値ではなくバイナリ値 (0 または 1) になることです。
ロジスティック回帰式の例を次に示します。
y = e^(b0 + b1*x) / (1 + e^(b0 + b1*x))
この方程式では:
- yは予測値 (または出力) です。
- b0はバイアス (または切片項) です。
- b1は入力の係数
- xは予測変数 (または入力) です。
従属変数は通常、 ベルヌーイ分布。 係数の値は、最尤推定 (MLE) 、勾配降下法、および確率的勾配降下法を使用して推定されます。
のような他の分類アルゴリズムと同様に、 k 最近傍、a 混同行列 ロジスティック回帰アルゴリズムの精度を評価するために使用されます。
知ってますか? ロジスティック回帰は、一般化線形モデル (GLM) のより大きなファミリの一部です。
分類器のパフォーマンスを評価するのと同じように、モデルが観測を特定の方法で分類した理由を知ることも同様に重要です。 言い換えれば、分類子の決定が解釈可能である必要があります。
解釈可能性を定義するのは簡単ではありませんが、その主な目的は、アルゴリズムが特定の決定を下した理由を人間が知る必要があるということです。 ロジスティック回帰の場合、次のような統計テストと組み合わせることができます。 ヴァルト検定 または 尤度比検定 解釈可能性のために。
ロジスティック回帰を使用する場合
ロジスティック回帰を適用して、カテゴリ従属変数を予測します。 つまり、予測がカテゴリカルである場合に使用されます。たとえば、yes または no、true または false、0 または 1 です。ロジスティック回帰の予測される確率または出力は、それらのいずれかである可能性があり、妥協点はありません。
予測変数の場合、次のいずれかのカテゴリの一部になる可能性があります。

- 連続データ:無限スケールで測定できるデータ。 2 つの数値の間の任意の値を取ることができます。 例としては、ポンド単位の重量や華氏単位の温度があります。
- 離散名義データ:名前付きカテゴリに適合するデータ。 簡単な例は髪の色です: 金髪、黒、または茶色。
- 離散順序データ:スケール上の何らかの順序に適合するデータ。 例として、製品またはサービスに対する満足度を 1 ~ 5 のスケールで示します。
ロジスティック回帰分析は、イベントの可能性を予測するのに役立ちます。 これは、任意の 2 つのクラス間の確率を決定するのに役立ちます。
簡単に言えば、履歴データを調べることで、ロジスティック回帰は次のことを予測できます。
- メールはスパムです
- 今日は雨が降るでしょう
- 腫瘍は致命的です
- 個人が車を購入する
- オンライン取引は詐欺です
- 出場者が選挙に勝つ
- ユーザーのグループが製品を購入します
- 保険契約者は、保険期間が満了する前に失効します
- プロモーション メールの受信者は、レスポンダーまたは非レスポンダーです。
本質的に、ロジスティック回帰は、確率と分類の問題を解決するのに役立ちます。 つまり、ロジスティック回帰からの分類と確率の結果のみを期待できます。
たとえば、何かが「真か偽か」の確率を決定したり、「はいまたはいいえ」のような 2 つの結果の間で決定したりするために使用できます。
ロジスティック回帰モデルは、抽出、変換、読み込み (ETL) 操作のデータを分類するのにも役立ちます。 観測値の数が特徴の数よりも少ない場合は、ロジスティック回帰を使用しないでください。 そうしないと、オーバーフィッティングにつながる可能性があります。
線形回帰とロジスティック回帰
ロジスティック回帰は、1 つ以上の独立変数のカテゴリ変数を予測しますが、 線形回帰 連続変数を予測します。 つまり、ロジスティック回帰は一定の出力を提供しますが、線形回帰は連続的な出力を提供します。
線形回帰では結果が連続であるため、結果の可能な値は無限にあります。 ただし、ロジスティック回帰の場合、可能な結果値の数は限られています。
線形回帰では、従属変数と独立変数は線形に関連している必要があります。 ロジスティック回帰の場合、独立変数は線形に関連している必要があります。 対数オッズ (ログ (p/(1-p)))。
ヒント:ロジスティック回帰は、R、Python、Java、MATLAB など、データ分析に使用される任意のプログラミング言語で実装できます。
線形回帰は通常の最小二乗法を使用して推定されますが、ロジスティック回帰は最尤推定アプローチを使用して推定されます。
ロジスティック回帰と線形回帰はどちらも 教師あり機械学習 アルゴリズムと回帰分析の 2 つの主なタイプ。 ロジスティック回帰は分類問題の解決に使用されますが、線形回帰は主に回帰問題に使用されます。
勉強に費やした時間の例に戻ると、線形回帰とロジスティック回帰は異なることを予測できます。 ロジスティック回帰は、学生が試験に合格したかどうかを予測するのに役立ちます。 対照的に、線形回帰は学生のスコアを予測できます。
ロジスティック回帰の仮定
ロジスティック回帰を使用する際に、いくつかの仮定を行います。 ロジスティック回帰を正しく使用して予測を行い、分類の問題を解決するには、仮定が不可欠です。
ロジスティック回帰の主な仮定は次のとおりです。
- 独立変数間の多重共線性はほとんどまたはまったくありません。
- 独立変数は、対数オッズ (対数 (p/(1-p))) に直線的に関連しています。
- 従属変数は二値またはバイナリです。 2 つの異なるカテゴリに分類されます。 これは、後で説明するバイナリ ロジスティック回帰にのみ適用されます。
- エラーにつながる可能性があるため、意味のない変数はありません。
- データ サンプルのサイズが大きくなり、より良い結果を得るために不可欠です。
- 外れ値はありません。
ロジスティック回帰の種類
ロジスティック回帰は、結果の数または従属変数のカテゴリに基づいて、さまざまなタイプに分類できます。
ロジスティック回帰について考えるとき、ほとんどの場合、バイナリ ロジスティック回帰を思い浮かべます。 この記事のほとんどの部分で、ロジスティック回帰について言及したとき、バイナリ ロジスティック回帰について言及していました。
以下は、ロジスティック回帰の 3 つの主なタイプです。
二項ロジスティック回帰
二項ロジスティック回帰は、従属変数と独立変数の間の関係を予測するために使用される統計的手法です。 この方法では、従属変数は 2 値変数です。つまり、2 つの値 (yes または no、true または false、成功または失敗、0 または 1) のみを取ることができます。
二項ロジスティック回帰の簡単な例は、電子メールがスパムかどうかを判断することです。
多項ロジスティック回帰
多項ロジスティック回帰は、バイナリ ロジスティック回帰の拡張です。 結果または従属変数の 3 つ以上のカテゴリが許可されます。
これはバイナリ ロジスティック回帰に似ていますが、2 つ以上の結果が考えられる場合があります。 これは、結果変数が 3 つ以上の可能な順序付けられていない型(量的な意味を持たない型) を持つことができることを意味します。 たとえば、従属変数は、「タイプ A」、「タイプ B」、または「タイプ C」を表す場合があります。
二項ロジスティック回帰と同様に、多項ロジスティック回帰も最尤推定を使用して確率を決定します。
たとえば、多項ロジスティック回帰を使用して、教育と職業選択の関係を調べることができます。 ここで、職業選択は、さまざまな職業のカテゴリで構成される従属変数になります。
順序ロジスティック回帰
順序ロジスティック回帰は、順序回帰としても知られ、バイナリ ロジスティック回帰の別の拡張です。 これは、従属変数を 3 つ以上の可能な順序付けられたタイプ(量的な意味を持つタイプ) で予測するために使用されます。 たとえば、従属変数は、「まったくそう思わない」、「そう思わない」、「そう思う」、または「強くそう思う」を表すことができる。
仕事のパフォーマンス (悪い、平均、または非常に良い) と仕事の満足度 (不満足、満足、または非常に満足) を判断するために使用できます。
ロジスティック回帰の長所と短所
ロジスティック回帰モデルの長所と短所の多くは、線形回帰モデルにも当てはまります。 ロジスティック回帰モデルの最も重要な利点の 1 つは、分類するだけでなく、確率も提供することです。
以下は、ロジスティック回帰アルゴリズムの利点の一部です。
- 理解しやすく、実装しやすく、トレーニングが効率的
- データセットが線形分離可能である場合にうまく機能します
- 小さいデータセットの精度が高い
- クラスの分布について何の仮定もしない
- 関連付けの方向性 (正または負) を提供します。
- 特徴間の関係を見つけるのに便利
- 十分に調整された確率を提供します
- 低次元のデータセットで過剰適合しにくい
- 多クラス分類に拡張可能
ただし、ロジスティック回帰には多くの欠点があります。 2 つのクラスを完全に分離する機能がある場合、モデルはそれ以上トレーニングできません。 これを完全分離といいます。
これは主に、最適な重みが無限になるため、その機能の重みが収束しないために発生します。 ただし、ほとんどの場合、完全な分離は、重みの事前確率分布を定義するか、重みのペナルティを導入することで解決できます。
以下は、ロジスティック回帰アルゴリズムの欠点の一部です。
- 線形境界を構築します
- 特徴の数が観測の数よりも多い場合、過剰適合につながる可能性があります
- 予測子には多重共線性が平均的であるか、またはまったくない必要があります
- 複雑な関係を得ることに挑戦します。 ニューラルネットワークのようなアルゴリズムはより適切で強力です
- 離散関数の予測にのみ使用可能
- 非線形問題が解けない
- 外れ値に敏感
人生に選択肢があるときは、ロジスティック回帰を考えてみてください
多くの人は、コンピューターとは異なり、人間はバイナリーの世界に住んでいないと主張するかもしれません。 もちろん、ピザとハンバーガーが与えられた場合は、どちらかを選択する必要はなく、両方を一口食べることができます。 しかし、よく見ると、(文字通り)すべてに二者択一が刻まれています。 ピザを食べるか食べないかを選択できます。 中間点はありません。
データ量が限られている場合、予測モデルのパフォーマンスを評価するのは難しい場合があります。 これには、使用可能なデータをトレーニング セットとテスト セットに分割するクロス検証と呼ばれる手法を使用できます。
