¿Qué es la regresión logística? Aprenda cuándo usarlo

La vida está llena de opciones binarias difíciles.

¿Debería tener esa porción de pizza o no? ¿Debo llevar paraguas o no?

Si bien algunas decisiones se pueden tomar correctamente sopesando los pros y los contras, por ejemplo, es mejor no comer una porción de pizza porque contiene calorías adicionales, algunas decisiones pueden no ser tan fáciles.

Por ejemplo, nunca puedes estar completamente seguro de si lloverá o no en un día específico. Así que la decisión de llevar o no un paraguas es difícil de tomar.

Para tomar la decisión correcta, se requieren capacidades predictivas. Esta habilidad es muy lucrativa y tiene numerosas aplicaciones en el mundo real, especialmente en computadoras. A las computadoras les encantan las decisiones binarias. Después de todo, hablan en código binario.

Aprendizaje automático   Los algoritmos, más precisamente el algoritmo de regresión logística , pueden ayudar a predecir la probabilidad de eventos al observar puntos de datos históricos. Por ejemplo, puede predecir si un individuo ganará las elecciones o si lloverá hoy.

Si se pregunta qué es el análisis de regresión , es un tipo de técnica de modelado predictivo que se utiliza para encontrar la relación entre una variable dependiente y una o más variables independientes.

Un ejemplo de variables independientes es el tiempo dedicado a estudiar y el tiempo dedicado a Instagram. En este caso, las calificaciones serán la variable dependiente. Esto se debe a que tanto el “tiempo dedicado a estudiar” como el “tiempo dedicado a Instagram” influirían en las calificaciones; uno positivamente y el otro negativamente.

La regresión logística es un algoritmo de clasificación que predice un resultado binario basado en una serie de variables independientes. En el ejemplo anterior, esto significaría predecir si aprobaría o reprobaría una clase. Por supuesto, la regresión logística también se puede usar para resolver problemas de regresión, pero se usa principalmente para problemas de clasificación.

Otro ejemplo sería predecir si un estudiante será aceptado en una universidad. Para eso, se considerarán múltiples factores como el puntaje del SAT, el promedio de calificaciones del estudiante y la cantidad de actividades extracurriculares. Utilizando datos históricos sobre resultados anteriores, el algoritmo de regresión logística clasificará a los estudiantes en categorías de "aceptación" o "rechazo".

La regresión logística también se conoce como regresión logística binomial o regresión logística binaria. Si hay más de dos clases de la variable de respuesta, se llama regresión logística multinomial . Como era de esperar, la regresión logística se tomó prestada de las estadísticas y es uno de los algoritmos de clasificación binaria más comunes en el aprendizaje automático y la ciencia de datos.

La regresión logística funciona midiendo la relación entre la variable dependiente (lo que queremos predecir) y una o más variables independientes (las características). Lo hace estimando las probabilidades con la ayuda de su función logística subyacente.

Términos clave en la regresión logística

Comprender la terminología es fundamental para descifrar correctamente los resultados de la regresión logística. Saber qué significan términos específicos lo ayudará a aprender rápidamente si es nuevo en estadísticas o aprendizaje automático.

¿Qué es una función logística?

La regresión logística lleva el nombre de la función utilizada en su núcleo, la función logística . Los estadísticos lo usaron inicialmente para describir las propiedades del crecimiento de la población. La función sigmoidea y la función logit son algunas variaciones de la función logística. La función logit es la inversa de la función logística estándar.

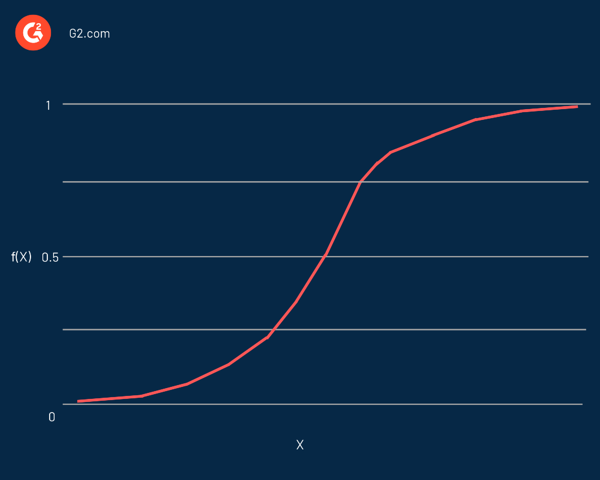
En efecto, es una curva en forma de S capaz de tomar cualquier número real y convertirlo en un valor entre 0 y 1, pero nunca precisamente en esos límites. Está representado por la ecuación:

En esta ecuación:

• f(X) es la salida de la función
• L es el valor máximo de la curva
• e es la base de los logaritmos naturales
• k es la pendiente de la curva
• x es el número real
• x0 son los valores x del punto medio sigmoide

Si el valor predicho es un valor negativo considerable, se considera cercano a cero. Por otro lado, si el valor predicho es un valor positivo significativo, se considera cercano a uno.

La regresión logística se representa de forma similar a cómo se define la regresión lineal utilizando la ecuación de una línea recta. Una diferencia notable de la regresión lineal es que la salida será un valor binario (0 o 1) en lugar de un valor numérico.

Aquí hay un ejemplo de una ecuación de regresión logística:

En esta ecuación:

• y es el valor predicho (o la salida)
• b0 es el sesgo (o el término de intersección)
• b1 es el coeficiente para la entrada
• x es la variable predictora (o la entrada)

La variable dependiente generalmente sigue la   Distribución de Bernoulli. Los valores de los coeficientes se estiman utilizando estimación de máxima verosimilitud (MLE) , descenso de gradiente y descenso de gradiente estocástico .

Al igual que con otros algoritmos de clasificación como el   k-vecinos más cercanos, a   matriz de confusión   se utiliza para evaluar la precisión del algoritmo de regresión logística.

Al igual que evaluar el desempeño de un clasificador, es igualmente importante saber por qué el modelo clasificó una observación de una manera particular. En otras palabras, necesitamos que la decisión del clasificador sea interpretable.

Aunque la interpretabilidad no es fácil de definir, su intención principal es que los humanos sepan por qué un algoritmo tomó una decisión en particular. En el caso de la regresión logística, se puede combinar con pruebas estadísticas como la   prueba de Wald   o el   prueba de razón de verosimilitud   para la interpretabilidad.

Cuándo usar la regresión logística

Se aplica la regresión logística para predecir la variable dependiente categórica. En otras palabras, se usa cuando la predicción es categórica, por ejemplo, sí o no, verdadero o falso, 0 o 1. La probabilidad pronosticada o el resultado de la regresión logística pueden ser cualquiera de ellos, y no hay término medio.

En el caso de las variables predictoras, pueden formar parte de alguna de las siguientes categorías:

• Datos continuos: datos que se pueden medir en una escala infinita. Puede tomar cualquier valor entre dos números. Los ejemplos son el peso en libras o la temperatura en Fahrenheit.
• Datos nominales discretos: Datos que encajan en categorías nombradas. Un ejemplo rápido es el color del cabello: rubio, negro o castaño.
• Datos discretos y ordinales: datos que encajan en algún tipo de orden en una escala. Un ejemplo es decir qué tan satisfecho está con un producto o servicio en una escala de uno a cinco.

El análisis de regresión logística es valioso para predecir la probabilidad de un evento. Ayuda a determinar las probabilidades entre dos clases.

En esencia, la regresión logística ayuda a resolver problemas de probabilidad y clasificación . En otras palabras, solo puede esperar resultados de clasificación y probabilidad de la regresión logística.

Por ejemplo, se puede utilizar para determinar la probabilidad de que algo sea "verdadero o falso" y también para decidir entre dos resultados como "sí o no".

Un modelo de regresión logística también puede ayudar a clasificar datos para operaciones de extracción, transformación y carga (ETL). La regresión logística no debe usarse si el número de observaciones es menor que el número de entidades. De lo contrario, puede dar lugar a un sobreajuste.

Regresión lineal frente a regresión logística

Mientras que la regresión logística predice la variable categórica para una o más variables independientes,   regresión lineal   predice la variable continua. En otras palabras, la regresión logística proporciona un resultado constante, mientras que la regresión lineal ofrece un resultado continuo.

Dado que el resultado es continuo en la regresión lineal, existen infinitos valores posibles para el resultado. Pero para la regresión logística, el número de posibles valores de resultado es limitado.

En la regresión lineal, las variables dependientes e independientes deben estar relacionadas linealmente. En el caso de la regresión logística, las variables independientes deben estar linealmente relacionadas con la   registro de probabilidades   (registro (p/(1-p)).

Mientras que la regresión lineal se estima utilizando el método de mínimos cuadrados ordinarios, la regresión logística se estima utilizando el enfoque de estimación de máxima verosimilitud.

Tanto la regresión logística como la lineal son   aprendizaje automático supervisado   algoritmos y los dos tipos principales de análisis de regresión. Mientras que la regresión logística se usa para resolver problemas de clasificación, la regresión lineal se usa principalmente para problemas de regresión.

Volviendo al ejemplo del tiempo dedicado al estudio, la regresión lineal y la regresión logística pueden predecir cosas diferentes. La regresión logística puede ayudar a predecir si el estudiante aprobó o no un examen. Por el contrario, la regresión lineal puede predecir la puntuación del estudiante.

Supuestos de regresión logística

Al usar la regresión logística, hacemos algunas suposiciones. Las suposiciones son integrales para usar correctamente la regresión logística para hacer predicciones y resolver problemas de clasificación.

Tipos de regresión logística

La regresión logística se puede dividir en diferentes tipos según el número de resultados o categorías de la variable dependiente.

Cuando pensamos en regresión logística, lo más probable es que pensemos en regresión logística binaria. En la mayor parte de este artículo, cuando nos referimos a la regresión logística, nos referimos a la regresión logística binaria.

Los siguientes son los tres tipos principales de regresión logística.

Regresión logística binaria

La regresión logística binaria es un método estadístico utilizado para predecir la relación entre una variable dependiente y una variable independiente. En este método, la variable dependiente es una variable binaria, lo que significa que solo puede tomar dos valores (sí o no, verdadero o falso, éxito o fracaso, 0 o 1).

Un ejemplo simple de regresión logística binaria es determinar si un correo electrónico es spam o no.

Regresión logística multinomial

La regresión logística multinomial es una extensión de la regresión logística binaria. Permite más de dos categorías del resultado o variable dependiente.

Es similar a la regresión logística binaria pero puede tener más de dos resultados posibles. Esto significa que la variable de resultado puede tener tres o más posibles tipos desordenados , tipos que no tienen importancia cuantitativa. Por ejemplo, la variable dependiente puede representar "Tipo A", "Tipo B" o "Tipo C".

Similar a la regresión logística binaria, la regresión logística multinomial también utiliza la estimación de máxima verosimilitud para determinar la probabilidad.

Por ejemplo, la regresión logística multinomial se puede utilizar para estudiar la relación entre la educación y las elecciones ocupacionales. Aquí, las elecciones ocupacionales serán la variable dependiente que consta de categorías de diferentes ocupaciones.

Regresión logística ordinal

La regresión logística ordinal , también conocida como regresión ordinal, es otra extensión de la regresión logística binaria. Se utiliza para predecir la variable dependiente con tres o más tipos ordenados posibles, tipos que tienen un significado cuantitativo. Por ejemplo, la variable dependiente puede representar "Muy en desacuerdo", "En desacuerdo", "De acuerdo" o "Muy de acuerdo".

Se puede utilizar para determinar el desempeño laboral (pobre, promedio o excelente) y la satisfacción laboral (insatisfecho, satisfecho o muy satisfecho).

Ventajas y desventajas de la regresión logística

Muchas de las ventajas y desventajas del modelo de regresión logística se aplican al modelo de regresión lineal. Una de las ventajas más significativas del modelo de regresión logística es que no solo clasifica sino que también da probabilidades.

Sin embargo, existen numerosas desventajas en la regresión logística. Si hay una característica que separaría dos clases perfectamente, entonces el modelo ya no se puede entrenar. Esto se llama separación completa .

Esto sucede principalmente porque el peso de esa función no convergería, ya que el peso óptimo sería infinito. Sin embargo, en la mayoría de los casos, la separación completa se puede resolver definiendo una distribución de probabilidad previa de los pesos o introduciendo una penalización de los pesos.

Cuando la vida te dé opciones, piensa en la regresión logística

Muchos podrían argumentar que los humanos no viven en un mundo binario, a diferencia de las computadoras. Por supuesto, si te dan un trozo de pizza y una hamburguesa, puedes probar ambos sin tener que elegir solo uno. Pero si lo miras más de cerca, una decisión binaria está grabada (literalmente) en todo. Puedes elegir comer o no comer una pizza; no hay término medio.

Evaluar el rendimiento de un modelo predictivo puede ser complicado si hay una cantidad limitada de datos. Para ello, puede utilizar una técnica denominada validación cruzada, que consiste en dividir los datos disponibles en un conjunto de entrenamiento y un conjunto de prueba.