Che cos'è la regressione logistica? Impara quando usarlo

La vita è piena di scelte binarie difficili.

Dovrei avere quella fetta di pizza o no? Devo portare un ombrello o no?

Mentre alcune decisioni possono essere prese giustamente soppesando i pro ei contro – ad esempio, è meglio non mangiare una fetta di pizza perché contiene calorie in più – alcune decisioni potrebbero non essere così facili.

Ad esempio, non puoi mai essere completamente sicuro se pioverà o meno in un giorno specifico. Quindi la decisione se portare o meno un ombrello è difficile da prendere.

Per fare la scelta giusta, sono necessarie capacità predittive. Questa capacità è altamente redditizia e ha numerose applicazioni nel mondo reale, specialmente nei computer. I computer amano le decisioni binarie. Dopotutto, parlano in codice binario.

Apprendimento automatico   gli algoritmi, più precisamente l' algoritmo di regressione logistica , possono aiutare a prevedere la probabilità di eventi osservando i punti dati storici. Ad esempio, può prevedere se un individuo vincerà le elezioni o se pioverà oggi.

Se ti stai chiedendo cos'è l'analisi di regressione , è un tipo di tecnica di modellazione predittiva utilizzata per trovare la relazione tra una variabile dipendente e una o più variabili indipendenti.

Un esempio di variabili indipendenti è il tempo dedicato allo studio e il tempo trascorso su Instagram. In questo caso, i voti saranno la variabile dipendente. Questo perché sia ​​il “tempo dedicato allo studio” che il “tempo trascorso su Instagram” influenzerebbero i voti; uno positivo e l'altro negativo.

La regressione logistica è un algoritmo di classificazione che prevede un risultato binario basato su una serie di variabili indipendenti. Nell'esempio sopra, questo significherebbe prevedere se passeresti o meno una classe. Naturalmente, la regressione logistica può essere utilizzata anche per risolvere problemi di regressione, ma viene utilizzata principalmente per problemi di classificazione.

Un altro esempio potrebbe essere prevedere se uno studente sarà accettato in un'università. Per questo, verranno presi in considerazione molteplici fattori come il punteggio SAT, la media dei voti dello studente e il numero di attività extracurriculari. Utilizzando i dati storici sui risultati precedenti, l'algoritmo di regressione logistica ordinerà gli studenti in categorie "accetta" o "rifiuta".

La regressione logistica viene anche definita regressione logistica binomiale o regressione logistica binaria. Se sono presenti più di due classi della variabile di risposta, si parla di regressione logistica multinomiale . Non sorprende che la regressione logistica sia stata presa in prestito dalla statistica ed è uno degli algoritmi di classificazione binaria più comuni nell'apprendimento automatico e nella scienza dei dati.

La regressione logistica funziona misurando la relazione tra la variabile dipendente (cosa vogliamo prevedere) e una o più variabili indipendenti (le caratteristiche). Lo fa stimando le probabilità con l'aiuto della sua funzione logistica sottostante.

Termini chiave nella regressione logistica

Comprendere la terminologia è fondamentale per decifrare correttamente i risultati della regressione logistica. Conoscere il significato di termini specifici ti aiuterà a imparare rapidamente se non conosci le statistiche o l'apprendimento automatico.

Che cos'è una funzione logistica?

La regressione logistica prende il nome dalla funzione utilizzata al suo interno, la funzione logistica . Gli statistici inizialmente lo usarono per descrivere le proprietà della crescita della popolazione. La funzione sigmoidea e la funzione logit sono alcune varianti della funzione logistica. La funzione Logit è l'inverso della funzione logistica standard.

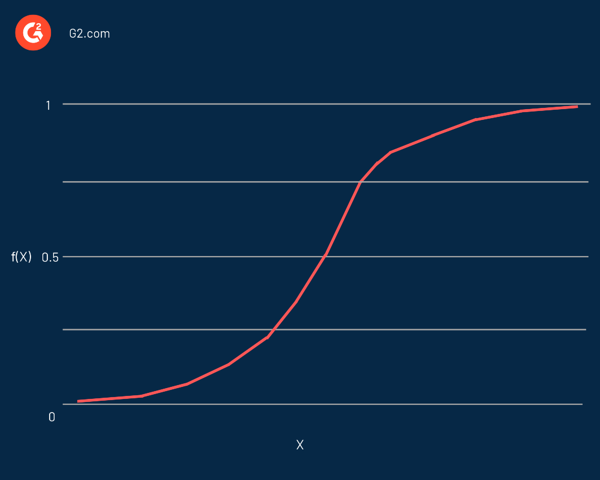
In effetti, è una curva a forma di S in grado di prendere qualsiasi numero reale e mapparlo in un valore compreso tra 0 e 1, ma mai esattamente a quei limiti. È rappresentato dall'equazione:

In questa equazione:

• f(X) è l'output della funzione
• L è il valore massimo della curva
• e è la base dei logaritmi naturali
• k è la pendenza della curva
• x è il numero reale
• x0 è il valore x del punto medio sigmoideo

Se il valore previsto è un valore notevolmente negativo, viene considerato prossimo allo zero. D'altra parte, se il valore previsto è un valore positivo significativo, viene considerato vicino a uno.

La regressione logistica è rappresentata in modo simile a come viene definita la regressione lineare utilizzando l'equazione di una retta. Una notevole differenza rispetto alla regressione lineare è che l'output sarà un valore binario (0 o 1) anziché un valore numerico.

Ecco un esempio di equazione di regressione logistica:

In questa equazione:

• y è il valore previsto (o l'output)
• b0 è il bias (o il termine di intercettazione)
• b1 è il coefficiente per l'input
• x è la variabile predittiva (o l'input)

La variabile dipendente generalmente segue il   distribuzione Bernoulliana. I valori dei coefficienti sono stimati utilizzando la stima di massima verosimiglianza (MLE) , la discesa del gradiente e la discesa del gradiente stocastico .

Come con altri algoritmi di classificazione come il   k-vicini più vicini, a   matrice di confusione   viene utilizzato per valutare l'accuratezza dell'algoritmo di regressione logistica.

Proprio come valutare le prestazioni di un classificatore, è altrettanto importante sapere perché il modello ha classificato un'osservazione in un modo particolare. In altre parole, abbiamo bisogno che la decisione del classificatore sia interpretabile.

Sebbene l'interpretabilità non sia facile da definire, il suo intento principale è che gli esseri umani dovrebbero sapere perché un algoritmo ha preso una decisione particolare. Nel caso della regressione logistica, può essere combinato con test statistici come il   Prova di Valdo   o il   test del rapporto di verosimiglianza   per interpretabilità.

Quando usare la regressione logistica

La regressione logistica viene applicata per prevedere la variabile dipendente categoriale. In altre parole, viene utilizzato quando la previsione è categorica, ad esempio sì o no, vero o falso, 0 o 1. La probabilità prevista o l'output della regressione logistica può essere uno di questi e non ci sono vie di mezzo.

Nel caso di variabili predittive, possono far parte di una delle seguenti categorie:

• Dati continui: dati che possono essere misurati su scala infinita. Può assumere qualsiasi valore compreso tra due numeri. Esempi sono il peso in libbre o la temperatura in Fahrenheit.
• Dati discreti e nominali: dati che rientrano in categorie denominate. Un rapido esempio è il colore dei capelli: biondo, nero o castano.
• Dati ordinali discreti: dati che rientrano in una qualche forma di ordine su una scala. Un esempio è dire quanto sei soddisfatto di un prodotto o servizio su una scala da uno a cinque.

L'analisi di regressione logistica è preziosa per prevedere la probabilità di un evento. Aiuta a determinare le probabilità tra due classi qualsiasi.

In sostanza, la regressione logistica aiuta a risolvere problemi di probabilità e classificazione . In altre parole, puoi aspettarti solo classificazione e risultati probabilistici dalla regressione logistica.

Ad esempio, può essere utilizzato per determinare la probabilità che qualcosa sia "vero o falso" e anche per decidere tra due risultati come "sì o no".

Un modello di regressione logistica può anche aiutare a classificare i dati per le operazioni di estrazione, trasformazione e caricamento (ETL). La regressione logistica non deve essere utilizzata se il numero di osservazioni è inferiore al numero di funzioni. In caso contrario, potrebbe causare un sovraadattamento.

Regressione lineare vs. regressione logistica

Mentre la regressione logistica prevede la variabile categoriale per una o più variabili indipendenti,   regressione lineare   predice la variabile continua. In altre parole, la regressione logistica fornisce un output costante, mentre la regressione lineare offre un output continuo.

Poiché il risultato è continuo nella regressione lineare, ci sono infiniti valori possibili per il risultato. Ma per la regressione logistica, il numero di possibili valori di esito è limitato.

Nella regressione lineare, le variabili dipendenti e indipendenti dovrebbero essere linearmente correlate. Nel caso della regressione logistica, le variabili indipendenti dovrebbero essere linearmente correlate a   log delle quote   (log (p/(1-p)).

Mentre la regressione lineare viene stimata utilizzando il metodo dei minimi quadrati ordinari, la regressione logistica viene stimata utilizzando l'approccio della stima della massima verosimiglianza.

Sia la regressione logistica che lineare lo sono   apprendimento automatico supervisionato   algoritmi e le due principali tipologie di analisi di regressione. Mentre la regressione logistica viene utilizzata per risolvere problemi di classificazione, la regressione lineare viene utilizzata principalmente per problemi di regressione.

Tornando all'esempio del tempo dedicato allo studio, la regressione lineare e la regressione logistica possono prevedere cose diverse. La regressione logistica può aiutare a prevedere se lo studente ha superato o meno un esame. Al contrario, la regressione lineare può prevedere il punteggio dello studente.

Ipotesi di regressione logistica

Durante l'utilizzo della regressione logistica, facciamo alcune ipotesi. Le ipotesi sono fondamentali per utilizzare correttamente la regressione logistica per fare previsioni e risolvere problemi di classificazione.

Tipi di regressione logistica

La regressione logistica può essere suddivisa in diversi tipi in base al numero di risultati o categorie della variabile dipendente.

Quando pensiamo alla regressione logistica, molto probabilmente pensiamo alla regressione logistica binaria. Nella maggior parte delle parti di questo articolo, quando ci riferivamo alla regressione logistica, ci riferivamo alla regressione logistica binaria.

I seguenti sono i tre tipi principali di regressione logistica.

Regressione logistica binaria

La regressione logistica binaria è un metodo statistico utilizzato per prevedere la relazione tra una variabile dipendente e una variabile indipendente. In questo metodo, la variabile dipendente è una variabile binaria, il che significa che può assumere solo due valori (sì o no, vero o falso, successo o fallimento, 0 o 1).

Un semplice esempio di regressione logistica binaria è determinare se un'e-mail è spam o meno.

Regressione logistica multinomiale

La regressione logistica multinomiale è un'estensione della regressione logistica binaria. Consente più di due categorie di risultato o variabile dipendente.

È simile alla regressione logistica binaria ma può avere più di due possibili risultati. Ciò significa che la variabile di risultato può avere tre o più possibili tipi non ordinati , tipi che non hanno significato quantitativo. Ad esempio, la variabile dipendente può rappresentare "Tipo A", "Tipo B" o "Tipo C".

Simile alla regressione logistica binaria, anche la regressione logistica multinomiale utilizza la stima di massima verosimiglianza per determinare la probabilità.

Ad esempio, la regressione logistica multinomiale può essere utilizzata per studiare la relazione tra la propria istruzione e le scelte occupazionali. Qui, le scelte occupazionali saranno la variabile dipendente che consiste in categorie di diverse occupazioni.

Regressione logistica ordinale

La regressione logistica ordinale , nota anche come regressione ordinale, è un'altra estensione della regressione logistica binaria. Viene utilizzato per prevedere la variabile dipendente con tre o più possibili tipi ordinati , tipi aventi un significato quantitativo. Ad esempio, la variabile dipendente può rappresentare "Fortemente in disaccordo", "Non sono d'accordo", "Accetto" o "Completamente d'accordo".

Può essere utilizzato per determinare la prestazione lavorativa (scarsa, media o eccellente) e la soddisfazione sul lavoro (insoddisfatta, soddisfatta o altamente soddisfatta).

Vantaggi e svantaggi della regressione logistica

Molti dei vantaggi e degli svantaggi del modello di regressione logistica si applicano al modello di regressione lineare. Uno dei vantaggi più significativi del modello di regressione logistica è che non solo classifica, ma fornisce anche probabilità.

Tuttavia, ci sono numerosi svantaggi nella regressione logistica. Se esiste una funzionalità che separerebbe perfettamente due classi, il modello non può più essere addestrato. Questa è chiamata separazione completa .

Ciò accade principalmente perché il peso per quella funzione non convergerebbe poiché il peso ottimale sarebbe infinito. Tuttavia, nella maggior parte dei casi, la separazione completa può essere risolta definendo una distribuzione di probabilità a priori dei pesi o introducendo una penalizzazione dei pesi.

Quando la vita ti offre opzioni, pensa alla regressione logistica

Molti potrebbero obiettare che gli esseri umani non vivono in un mondo binario, a differenza dei computer. Certo, se ti viene data una fetta di pizza e un hamburger, puoi prendere un boccone di entrambi senza doverne scegliere solo uno. Ma se lo guardi più da vicino, una decisione binaria è incisa (letteralmente) su tutto. Puoi scegliere di mangiare o non mangiare una pizza; non ci sono vie di mezzo.

Valutare le prestazioni di un modello predittivo può essere complicato se la quantità di dati è limitata. A tale scopo, è possibile utilizzare una tecnica chiamata convalida incrociata, che prevede il partizionamento dei dati disponibili in un set di addestramento e in un set di test.