การถดถอยโลจิสติกคืออะไร? เรียนรู้ว่าควรใช้เมื่อใด

ชีวิตเต็มไปด้วยตัวเลือกไบนารีที่ยากลำบาก

ฉันควรมีพิซซ่าชิ้นนั้นหรือไม่? ฉันควรพกร่มหรือไม่?

แม้ว่าการตัดสินใจบางอย่างจะทำได้ถูกต้องโดยการชั่งน้ำหนักข้อดีและข้อเสีย เช่น ไม่ควรกินพิซซ่าสักชิ้นเพราะมันมีแคลอรีมากเป็นพิเศษ การตัดสินใจบางอย่างอาจไม่ง่ายขนาดนั้น

ตัวอย่างเช่น คุณไม่สามารถแน่ใจได้อย่างเต็มที่ว่าฝนจะตกในวันใดวันหนึ่งหรือไม่ ดังนั้นการตัดสินใจว่าจะพกร่มหรือไม่จึงเป็นเรื่องยาก

ในการตัดสินใจเลือกที่ถูกต้อง จำเป็นต้องมีความสามารถในการคาดการณ์ ความสามารถนี้มีกำไรสูงและมีแอพพลิเคชั่นในโลกแห่งความเป็นจริงมากมาย โดยเฉพาะในคอมพิวเตอร์ คอมพิวเตอร์ชอบการตัดสินใจแบบไบนารี ท้ายที่สุดพวกเขาพูดด้วยรหัสไบนารี

การเรียนรู้ของเครื่อง   อัลกอริธึม ซึ่งเป็น อัลกอริธึมการถดถอยโลจิสติก ที่แม่นยำยิ่งขึ้น สามารถช่วยทำนายความเป็นไปได้ของเหตุการณ์โดยดูจากจุดข้อมูลในอดีต ตัวอย่างเช่น สามารถทำนายได้ว่าบุคคลใดจะชนะการเลือกตั้งหรือฝนจะตกในวันนี้

หากคุณสงสัยว่า การวิเคราะห์การถดถอย คืออะไร มันคือเทคนิคการสร้างแบบจำลองเชิงคาดการณ์ประเภทหนึ่งที่ใช้เพื่อค้นหาความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระอย่างน้อยหนึ่งตัว

ตัวอย่างของตัวแปรอิสระคือเวลาที่ใช้ในการศึกษาและเวลาที่ใช้ใน Instagram ในกรณีนี้ เกรดจะเป็นตัวแปรตาม ทั้งนี้เพราะทั้ง “เวลาที่ใช้เรียน” และ “เวลาที่ใช้ใน Instagram” จะส่งผลต่อเกรด หนึ่งบวกและอื่น ๆ ในเชิงลบ

Logistic regression เป็น อัลกอริธึมการจำแนกประเภท ที่ทำนายผลลัพธ์ไบนารีตามชุดของตัวแปรอิสระ ในตัวอย่างข้างต้น นี่จะหมายถึงการคาดเดาว่าคุณจะผ่านหรือล้มเหลวในชั้นเรียน แน่นอนว่า การถดถอยโลจิสติกยังสามารถใช้เพื่อแก้ปัญหาการถดถอยได้ แต่ส่วนใหญ่จะใช้สำหรับปัญหาการจำแนกประเภท

อีกตัวอย่างหนึ่งคือการทำนายว่านักศึกษาจะเข้ามหาวิทยาลัยหรือไม่ ด้วยเหตุนี้ จะพิจารณาปัจจัยหลายประการ เช่น คะแนน SAT คะแนนเฉลี่ยของนักเรียน และจำนวนกิจกรรมนอกหลักสูตร การใช้ข้อมูลในอดีตเกี่ยวกับผลลัพธ์ก่อนหน้า อัลกอริธึมการถดถอยโลจิสติกจะจัดเรียงนักเรียนเป็นหมวดหมู่ "ยอมรับ" หรือ "ปฏิเสธ"

การถดถอยโลจิสติกเรียกอีกอย่างว่าการถดถอยโลจิสติกแบบทวินามหรือการถดถอยโลจิสติกแบบไบนารี หากมีตัวแปรตอบกลับมากกว่า 2 คลาส จะเรียกว่า multinomial logistic regression ไม่น่าแปลกใจเลยที่การถดถอยโลจิสติกถูกยืมมาจากสถิติและเป็นหนึ่งในอัลกอริธึมการจำแนกประเภทไบนารีที่พบบ่อยที่สุดในการเรียนรู้ของเครื่องและวิทยาศาสตร์ข้อมูล

การถดถอยโลจิสติกทำงานโดยการวัดความสัมพันธ์ระหว่างตัวแปรตาม (สิ่งที่เราต้องการทำนาย) กับตัวแปรอิสระอย่างน้อยหนึ่งตัว (คุณสมบัติ) ทำได้โดยการประเมินความน่าจะเป็นด้วยความช่วยเหลือของฟังก์ชันลอจิสติกส์พื้นฐาน

คำศัพท์สำคัญในการถดถอยโลจิสติก

การทำความเข้าใจคำศัพท์เป็นสิ่งสำคัญในการถอดรหัสผลลัพธ์ของการถดถอยโลจิสติกอย่างเหมาะสม การรู้ว่าคำศัพท์เฉพาะหมายถึงอะไรจะช่วยให้คุณเรียนรู้ได้อย่างรวดเร็ว หากคุณเพิ่งเริ่มใช้สถิติหรือแมชชีนเลิร์นนิง

ฟังก์ชันลอจิสติกส์คืออะไร?

การถดถอยโลจิสติกตั้งชื่อตามฟังก์ชันที่ใช้ในหัวใจ นั่นคือ ฟังก์ชันลอจิสติกส์ นักสถิติเริ่มใช้เพื่ออธิบายคุณสมบัติของการเติบโตของประชากร ฟังก์ชันซิกมอยด์ และ ฟังก์ชัน ลอจิทเป็นรูปแบบหนึ่งของฟังก์ชันลอจิสติกส์ ฟังก์ชัน Logit เป็นฟังก์ชันผกผันของฟังก์ชันลอจิสติกมาตรฐาน

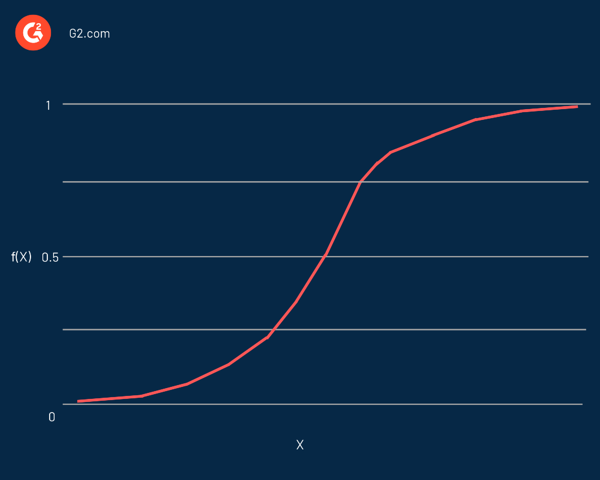
ผลก็คือ มันเป็นเส้นโค้งรูปตัว S ที่สามารถนำจำนวนจริงใดๆ มาจับคู่เป็นค่าระหว่าง 0 ถึง 1 ได้ แต่จะไม่มีวันแม่นยำที่ขีดจำกัดเหล่านั้น มันถูกแสดงโดยสมการ:

ในสมการนี้:

• f(X) คือเอาต์พุตของฟังก์ชัน
• L คือค่าสูงสุดของเส้นโค้ง
• e เป็นฐานของลอการิทึมธรรมชาติ
• k คือความชันของเส้นโค้ง
• x คือจำนวนจริง
• x0 คือค่า x ของจุดกึ่งกลางซิกมอยด์

หากค่าที่คาดการณ์ไว้เป็นค่าลบมาก จะถือว่าใกล้ศูนย์ ในทางกลับกัน หากค่าที่คาดการณ์ไว้เป็นค่าบวกที่มีนัยสำคัญ ก็จะถือว่ามีค่าใกล้เคียงกับค่าหนึ่ง

การถดถอยโลจิสติกจะแสดงคล้ายกับวิธีกำหนดถดถอยเชิงเส้นโดยใช้สมการของเส้นตรง ความแตกต่างที่โดดเด่นจากการถดถอยเชิงเส้นคือผลลัพธ์จะเป็นค่าไบนารี (0 หรือ 1) แทนที่จะเป็นค่าตัวเลข

ต่อไปนี้คือตัวอย่างสมการถดถอยโลจิสติก:

ในสมการนี้:

• y คือค่าที่คาดการณ์ไว้ (หรือผลลัพธ์)
• b0 คืออคติ (หรือระยะการสกัดกั้น)
• b1 คือสัมประสิทธิ์ของอินพุต
• x เป็นตัวแปรทำนาย (หรืออินพุต)

ตัวแปรตามโดยทั่วไปจะตามหลัง   การกระจายเบอร์นูลลี ค่าของสัมประสิทธิ์ถูกประมาณโดยใช้การประมาณความน่าจะเป็น สูงสุด (MLE) การ ไล่ระดับสีแบบ เกรเดียนต์ และ การไล่ระดับสีแบบสุ่ม

เช่นเดียวกับอัลกอริธึมการจำแนกประเภทอื่นๆ เช่น the   k-เพื่อนบ้านที่ใกล้ที่สุด, a   เมทริกซ์ความสับสน   ใช้ในการประเมินความถูกต้องของอัลกอริทึมการถดถอยโลจิสติก

เช่นเดียวกับการประเมินประสิทธิภาพของตัวแยกประเภท การรู้ว่าเหตุใดตัวแบบจึงจำแนกการสังเกตในลักษณะเฉพาะก็สำคัญไม่แพ้กัน กล่าวอีกนัยหนึ่ง เราต้องการการตัดสินใจของผู้แยกประเภทเพื่อให้สามารถตีความได้

แม้ว่าความสามารถในการตีความจะไม่ใช่เรื่องง่ายที่จะกำหนด แต่จุดประสงค์หลักก็คือมนุษย์ควรรู้ว่าเหตุใดอัลกอริทึมจึงตัดสินใจโดยเฉพาะ ในกรณีของการถดถอยโลจิสติก สามารถรวมกับการทดสอบทางสถิติเช่น   การทดสอบ Wald   หรือ   การทดสอบอัตราส่วนความน่าจะเป็น   เพื่อการตีความ

เมื่อใดควรใช้การถดถอยโลจิสติก

การถดถอยโลจิสติกใช้เพื่อทำนายตัวแปรตามหมวดหมู่ กล่าวอีกนัยหนึ่ง จะใช้เมื่อการคาดการณ์เป็นหมวดหมู่ เช่น ใช่หรือไม่ใช่ จริงหรือเท็จ 0 หรือ 1 ความน่าจะเป็นที่คาดการณ์หรือผลลัพธ์ของการถดถอยโลจิสติกสามารถเป็นหนึ่งในนั้น และไม่มีจุดกึ่งกลาง

ในกรณีของตัวแปรทำนาย พวกเขาสามารถเป็นส่วนหนึ่งของหมวดหมู่ใด ๆ ต่อไปนี้:

• ข้อมูลต่อเนื่อง: ข้อมูลที่สามารถวัดได้ในระดับอนันต์ สามารถใช้ค่าใดก็ได้ระหว่างตัวเลขสองตัว ตัวอย่างคือน้ำหนักเป็นปอนด์หรืออุณหภูมิเป็นฟาเรนไฮต์
• ข้อมูลที่ไม่ต่อเนื่องและระบุ: ข้อมูลที่เหมาะกับหมวดหมู่ที่มีชื่อ ตัวอย่างสั้นๆ คือ สีผม: สีบลอนด์ สีดำ หรือสีน้ำตาล
• ข้อมูลลำดับที่ไม่ต่อเนื่อง: ข้อมูลที่พอดีกับรูปแบบการเรียงลำดับบางอย่างบนมาตราส่วน ตัวอย่างคือการบอกว่าคุณพอใจกับผลิตภัณฑ์หรือบริการเพียงใดในระดับหนึ่งถึงห้า

การวิเคราะห์การถดถอยโลจิสติกมีค่าสำหรับการทำนายความน่าจะเป็นของเหตุการณ์ ช่วยกำหนดความน่าจะเป็นระหว่างสองคลาสใด ๆ

โดยพื้นฐานแล้ว การถดถอยโลจิสติกช่วยแก้ปัญหา ความน่าจะ เป็นและปัญหา การจำแนกประเภท กล่าวอีกนัยหนึ่ง คุณสามารถคาดหวังเฉพาะผลการจำแนกประเภทและความน่าจะเป็นจากการถดถอยโลจิสติก

ตัวอย่างเช่น สามารถใช้เพื่อกำหนดความน่าจะเป็นของบางสิ่งที่ "จริงหรือเท็จ" และสำหรับการตัดสินใจระหว่างผลลัพธ์สองอย่าง เช่น "ใช่หรือไม่ใช่"

แบบจำลองการถดถอยโลจิสติกยังช่วยจัดประเภทข้อมูลสำหรับการดำเนินการแยก แปลง และโหลด (ETL) ไม่ควรใช้การถดถอยโลจิสติกหากจำนวนการสังเกตน้อยกว่าจำนวนจุดสนใจ มิเช่นนั้นอาจนำไปสู่การสวมใส่มากเกินไป

การถดถอยเชิงเส้นกับการถดถอยโลจิสติก

ในขณะที่การถดถอยโลจิสติกทำนายตัวแปรหมวดหมู่สำหรับตัวแปรอิสระตั้งแต่หนึ่งตัวขึ้นไป   การถดถอยเชิงเส้น   ทำนายตัวแปรต่อเนื่อง กล่าวอีกนัยหนึ่งการถดถอยโลจิสติกให้เอาต์พุตคงที่ในขณะที่การถดถอยเชิงเส้นให้เอาต์พุตต่อเนื่อง

เนื่องจากผลลัพธ์มีความต่อเนื่องในการถดถอยเชิงเส้น จึงมีค่าที่เป็นไปได้อนันต์สำหรับผลลัพธ์ แต่สำหรับการถดถอยโลจิสติก จำนวนของค่าผลลัพธ์ที่เป็นไปได้มีจำกัด

ในการถดถอยเชิงเส้น ตัวแปรตามและตัวแปรอิสระควรสัมพันธ์เชิงเส้น ในกรณีของการถดถอยโลจิสติก ตัวแปรอิสระควรสัมพันธ์เชิงเส้นกับ   เข้าสู่ระบบราคา   (บันทึก (p/(1-p))

ในขณะที่การถดถอยเชิงเส้นถูกประเมินโดยใช้วิธีกำลังสองน้อยที่สุดธรรมดา การถดถอยโลจิสติกถูกประเมินโดยใช้วิธีการประมาณค่าความน่าจะเป็นสูงสุด

ทั้งโลจิสติกและการถดถอยเชิงเส้นคือ   แมชชีนเลิร์นนิงภายใต้การดูแล   อัลกอริทึมและการวิเคราะห์การถดถอยสองประเภทหลัก ในขณะที่การถดถอยโลจิสติกใช้เพื่อแก้ปัญหาการจำแนกประเภท การถดถอยเชิงเส้นมักใช้สำหรับปัญหาการถดถอย

ย้อนกลับไปที่ตัวอย่างเวลาที่ใช้ในการศึกษา การถดถอยเชิงเส้นและการถดถอยโลจิสติกสามารถทำนายสิ่งต่าง ๆ ได้ Logistic regression ช่วยทำนายว่านักเรียนสอบผ่านหรือไม่ ในทางตรงกันข้าม การถดถอยเชิงเส้นสามารถทำนายคะแนนของนักเรียนได้

สมมติฐานการถดถอยโลจิสติก

ในขณะที่ใช้การถดถอยโลจิสติก เราตั้งสมมติฐานสองสามข้อ สมมติฐานเป็นส่วนสำคัญในการใช้การถดถอยโลจิสติกอย่างถูกต้องสำหรับการคาดการณ์และแก้ปัญหาการจำแนกประเภท

ประเภทของการถดถอยโลจิสติก

การถดถอยโลจิสติกสามารถแบ่งออกเป็นประเภทต่างๆ ตามจำนวนผลลัพธ์หรือหมวดหมู่ของตัวแปรตาม

เมื่อเราคิดถึงการถดถอยโลจิสติก เราอาจนึกถึงการถดถอยโลจิสติกแบบไบนารี ในส่วนใหญ่ของบทความนี้ เมื่อเราอ้างถึงการถดถอยโลจิสติก เราหมายถึงการถดถอยโลจิสติกแบบไบนารี

ต่อไปนี้เป็นสามประเภทหลักของการถดถอยโลจิสติก

การถดถอยโลจิสติกแบบไบนารี

การถดถอยโลจิสติกแบบไบนารี เป็นวิธีการทางสถิติที่ใช้ในการทำนายความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระ ในวิธีนี้ ตัวแปรตามเป็นตัวแปรไบนารี ซึ่งหมายความว่าสามารถรับได้เพียงสองค่าเท่านั้น (ใช่หรือไม่ใช่ จริงหรือเท็จ สำเร็จหรือล้มเหลว 0 หรือ 1)

ตัวอย่างง่ายๆ ของการถดถอยโลจิสติกแบบไบนารีคือการพิจารณาว่าอีเมลเป็นสแปมหรือไม่

การถดถอยโลจิสติกพหุนาม

การถดถอยโลจิสติกพหุนาม เป็นส่วนเสริมของการถดถอยโลจิสติกแบบไบนารี อนุญาตให้มีผลลัพธ์หรือตัวแปรตามมากกว่าสองหมวดหมู่

คล้ายกับการถดถอยโลจิสติกแบบไบนารี แต่สามารถมีผลลัพธ์ที่เป็นไปได้มากกว่าสองรายการ ซึ่งหมายความว่าตัวแปรผลลัพธ์สามารถมีประเภทที่ ไม่เรียงลำดับที่เป็นไปได้สามประเภท ขึ้นไป - ประเภทที่ไม่มีนัยสำคัญเชิงปริมาณ ตัวอย่างเช่น ตัวแปรตามอาจแสดงถึง "ประเภท A" "ประเภท B" หรือ "ประเภท C"

คล้ายกับการถดถอยโลจิสติกแบบไบนารี การถดถอยโลจิสติกพหุนามยังใช้การประมาณความน่าจะเป็นสูงสุดเพื่อกำหนดความน่าจะเป็น

ตัวอย่างเช่น สามารถใช้การถดถอยโลจิสติกพหุนามเพื่อศึกษาความสัมพันธ์ระหว่างการศึกษาและการเลือกอาชีพ ในที่นี้ การเลือกอาชีพจะเป็นตัวแปรตามซึ่งประกอบด้วยประเภทอาชีพต่างๆ

ลำดับการถดถอยโลจิสติก

การถดถอยโลจิสติกแบบ มีลำดับ หรือที่เรียกว่า การถดถอยแบบมีลำดับ เป็นอีกส่วนขยายของการถดถอยโลจิสติกแบบไบนารี ใช้เพื่อทำนายตัวแปรตามที่มี ประเภทเรียงลำดับที่เป็นไปได้สามประเภท ขึ้นไป - ประเภทที่มีนัยสำคัญเชิงปริมาณ ตัวอย่างเช่น ตัวแปรตามอาจแสดงถึง "ไม่เห็นด้วยอย่างยิ่ง" "ไม่เห็นด้วย" "เห็นด้วย" หรือ "เห็นด้วยอย่างยิ่ง"

สามารถใช้เพื่อกำหนดผลการปฏิบัติงาน (แย่ ปานกลาง หรือดีเยี่ยม) และความพึงพอใจในงาน (ไม่พอใจ พอใจ หรือพอใจมาก)

ข้อดีและข้อเสียของการถดถอยโลจิสติก

ข้อดีและข้อเสียหลายประการของตัวแบบการถดถอยโลจิสติกนำไปใช้กับตัวแบบการถดถอยเชิงเส้น ข้อดีที่สำคัญที่สุดประการหนึ่งของแบบจำลองการถดถอยโลจิสติกคือไม่เพียงจัดประเภท แต่ยังให้ความน่าจะเป็นด้วย

อย่างไรก็ตาม มีข้อเสียมากมายในการถดถอยโลจิสติก หากมีคุณสมบัติที่จะแยกสองคลาสได้อย่างสมบูรณ์ โมเดลนั้นจะไม่สามารถฝึกได้อีกต่อไป นี้เรียกว่า การแยกที่สมบูรณ์

สิ่งนี้เกิดขึ้นส่วนใหญ่เนื่องจากน้ำหนักสำหรับคุณลักษณะนั้นจะไม่มาบรรจบกันเนื่องจากน้ำหนักที่เหมาะสมที่สุดจะไม่มีที่สิ้นสุด อย่างไรก็ตาม ในกรณีส่วนใหญ่ การแยกโดยสมบูรณ์สามารถแก้ไขได้โดยการกำหนดการกระจายความน่าจะเป็นของตุ้มน้ำหนักก่อนหรือแนะนำการปรับลดตุ้มน้ำหนัก

เมื่อชีวิตให้ทางเลือกแก่คุณ ให้นึกถึงการถดถอยโลจิสติก

หลายคนอาจโต้แย้งว่ามนุษย์ไม่ได้อยู่ในโลกเลขฐานสอง ต่างจากคอมพิวเตอร์ แน่นอน ถ้าคุณได้รับพิซซ่าและแฮมเบอร์เกอร์ชิ้นหนึ่ง คุณสามารถทานทั้งสองอย่างโดยไม่ต้องเลือกเพียงอย่างใดอย่างหนึ่ง แต่ถ้าคุณมองให้ละเอียดยิ่งขึ้น การตัดสินใจแบบไบนารีจะถูกจารึกไว้บนทุกสิ่ง (ตามตัวอักษร) คุณสามารถเลือกที่จะกินหรือไม่กินพิซซ่า ไม่มีพื้นกลาง

การประเมินประสิทธิภาพของแบบจำลองการคาดการณ์อาจเป็นเรื่องยากหากมีข้อมูลจำนวนจำกัด สำหรับสิ่งนี้ คุณสามารถใช้เทคนิคที่เรียกว่า cross-validation ซึ่งเกี่ยวข้องกับการแบ่งพาร์ติชั่นข้อมูลที่มีอยู่ออกเป็นชุดการฝึกและชุดทดสอบ