ما هو الانحدار اللوجستي؟ تعلم متى تستخدمها

الحياة مليئة بالخيارات الثنائية الصعبة.

هل يجب أن أتناول شريحة البيتزا هذه أم لا؟ هل أحمل مظلة أم لا؟

في حين يمكن اتخاذ بعض القرارات بشكل صحيح من خلال الموازنة بين الإيجابيات والسلبيات - على سبيل المثال ، من الأفضل عدم تناول شريحة من البيتزا لأنها تحتوي على سعرات حرارية إضافية - قد لا تكون بعض القرارات بهذه السهولة.

على سبيل المثال ، لا يمكنك أن تكون متأكدًا تمامًا مما إذا كانت السماء ستمطر في يوم معين أم لا. لذا فإن قرار حمل المظلة من عدمه هو قرار صعب اتخاذه.

لاتخاذ القرار الصحيح ، يتطلب المرء قدرات تنبؤية. هذه القدرة مربحة للغاية ولها العديد من التطبيقات الواقعية ، خاصة في أجهزة الكمبيوتر. أجهزة الكمبيوتر تحب القرارات الثنائية. بعد كل شيء ، يتحدثون في رمز ثنائي.

التعلم الالي   يمكن أن تساعد الخوارزميات ، وبشكل أكثر دقة خوارزمية الانحدار اللوجستي ، في التنبؤ باحتمالية الأحداث من خلال النظر في نقاط البيانات التاريخية. على سبيل المثال ، يمكنها التنبؤ بما إذا كان الفرد سيفوز في الانتخابات أم ستمطر اليوم.

إذا كنت تتساءل عن ماهية تحليل الانحدار ، فهو نوع من تقنيات النمذجة التنبؤية المستخدمة للعثور على العلاقة بين متغير تابع ومتغير واحد أو أكثر من المتغيرات المستقلة.

مثال على المتغيرات المستقلة هو الوقت الذي تقضيه في الدراسة والوقت الذي يقضيه في Instagram. في هذه الحالة ، ستكون الدرجات هي المتغير التابع. وذلك لأن كلاً من "الوقت المستغرق في الدراسة" و "الوقت الذي يقضيه المستخدم على Instagram" سيؤثر على الدرجات ؛ أحدهما إيجابيا والآخر سلبا.

الانحدار اللوجستي هو خوارزمية تصنيف تتنبأ بنتيجة ثنائية بناءً على سلسلة من المتغيرات المستقلة. في المثال أعلاه ، قد يعني هذا التنبؤ بما إذا كنت ستنجح في فصل دراسي أم ستفشل فيه. بالطبع ، يمكن أيضًا استخدام الانحدار اللوجستي لحل مشاكل الانحدار ، ولكنه يستخدم بشكل أساسي لمشاكل التصنيف.

مثال آخر هو توقع ما إذا كان سيتم قبول الطالب في إحدى الجامعات. لذلك ، سيتم النظر في عوامل متعددة مثل درجة SAT ومتوسط ​​درجة الطالب وعدد الأنشطة اللامنهجية. باستخدام البيانات التاريخية حول النتائج السابقة ، ستقوم خوارزمية الانحدار اللوجستي بفرز الطلاب في فئات "قبول" أو "رفض".

يشار إلى الانحدار اللوجستي أيضًا باسم الانحدار اللوجستي ذي الحدين أو الانحدار اللوجستي الثنائي. إذا كان هناك أكثر من فئتين من متغير الاستجابة ، فإنه يسمى الانحدار اللوجستي متعدد الحدود . مما لا يثير الدهشة ، تم استعارة الانحدار اللوجستي من الإحصائيات وهو أحد أكثر خوارزميات التصنيف الثنائي شيوعًا في التعلم الآلي وعلم البيانات.

يعمل الانحدار اللوجستي عن طريق قياس العلاقة بين المتغير التابع (ما نريد التنبؤ به) ومتغير واحد أو أكثر (الميزات). يقوم بذلك عن طريق تقدير الاحتمالات بمساعدة وظيفته اللوجستية الأساسية.

المصطلحات الأساسية في الانحدار اللوجستي

فهم المصطلحات أمر بالغ الأهمية لفك نتائج الانحدار اللوجستي بشكل صحيح. ستساعدك معرفة ما تعنيه المصطلحات المحددة على التعلم بسرعة إذا كنت جديدًا في مجال الإحصاء أو التعلم الآلي.

ما هي الوظيفة اللوجستية؟

يُطلق على الانحدار اللوجستي اسم الوظيفة المستخدمة في جوهرها ، الوظيفة اللوجستية . استخدمه الإحصائيون في البداية لوصف خصائص النمو السكاني. تعد الوظيفة السينية ووظيفة السجل بعض الاختلافات في الوظيفة اللوجستية. دالة اللوجيت هي عكس الوظيفة اللوجيستية القياسية.

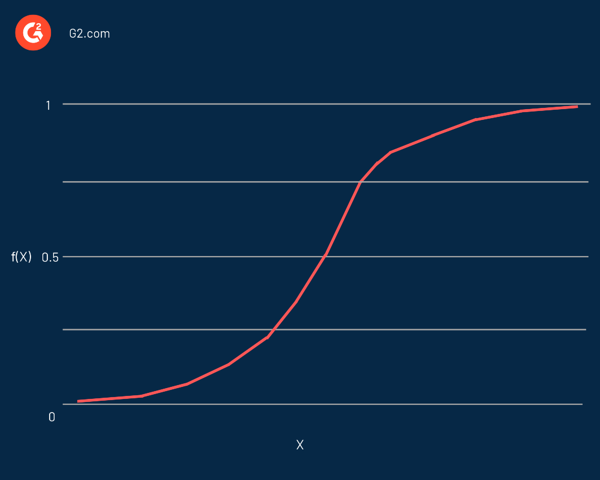
في الواقع ، إنه منحنى على شكل حرف S قادر على أخذ أي رقم حقيقي وتعيينه إلى قيمة بين 0 و 1 ، ولكن ليس بالضبط عند هذه الحدود. يتم تمثيلها بالمعادلة:

في هذه المعادلة:

• f (X) هو ناتج الوظيفة
• L هي القيمة القصوى للمنحنى
• البريد هو أساس اللوغاريتمات الطبيعية
• k هو انحدار المنحنى
• x هو الرقم الحقيقي
• x0 هي قيم x لنقطة المنتصف السيني

إذا كانت القيمة المتوقعة قيمة سالبة كبيرة ، فإنها تعتبر قريبة من الصفر. من ناحية أخرى ، إذا كانت القيمة المتوقعة قيمة موجبة كبيرة ، فإنها تعتبر قريبة من القيمة.

يتم تمثيل الانحدار اللوجستي بطريقة مشابهة لكيفية تعريف الانحدار الخطي باستخدام معادلة الخط المستقيم. الاختلاف الملحوظ عن الانحدار الخطي هو أن الناتج سيكون قيمة ثنائية (0 أو 1) بدلاً من قيمة عددية.

فيما يلي مثال على معادلة الانحدار اللوجستي:

في هذه المعادلة:

• y هي القيمة المتوقعة (أو الإخراج)
• b0 هو التحيز (أو مصطلح التقاطع)
• b1 هو معامل الإدخال
• x هو متغير التوقع (أو الإدخال)

المتغير التابع يتبع بشكل عام   توزيع برنولي. يتم تقدير قيم المعاملات باستخدام تقدير الاحتمالية القصوى (MLE) ، ونسب التدرج ، ونسب التدرج العشوائي .

كما هو الحال مع خوارزميات التصنيف الأخرى مثل   ك- أقرب الجيران ، أ   الارتباك مصفوفة   يستخدم لتقييم دقة خوارزمية الانحدار اللوجستي.

تمامًا مثل تقييم أداء المصنف ، من المهم أيضًا معرفة سبب تصنيف النموذج لملاحظة بطريقة معينة. بعبارة أخرى ، نحن بحاجة إلى أن يكون قرار المصنف قابلاً للتفسير.

على الرغم من أنه ليس من السهل تحديد القابلية للتفسير ، إلا أن هدفها الأساسي هو أن يعرف البشر سبب اتخاذ الخوارزمية قرارًا معينًا. في حالة الانحدار اللوجستي ، يمكن دمجه مع الاختبارات الإحصائية مثل   اختبار والد   أو ال   اختبار نسبة الاحتمالية   للتفسير.

متى تستخدم الانحدار اللوجستي

يتم تطبيق الانحدار اللوجستي للتنبؤ بالمتغير التابع الفئوي. بمعنى آخر ، يتم استخدامه عندما يكون التنبؤ فئويًا ، على سبيل المثال ، نعم أو لا ، صحيح أو خطأ ، 0 أو 1. يمكن أن يكون الاحتمال أو ناتج الانحدار اللوجستي أحدهما ، ولا يوجد حل وسط.

في حالة متغيرات التوقع ، يمكن أن تكون جزءًا من أي من الفئات التالية:

• البيانات المستمرة: البيانات التي يمكن قياسها على نطاق غير محدود. يمكن أن يأخذ أي قيمة بين رقمين. ومن الأمثلة الوزن بالجنيه أو درجة الحرارة بالفهرنهايت.
• البيانات الاسمية المنفصلة: البيانات التي تتناسب مع الفئات المسماة. ومن الأمثلة السريعة على ذلك لون الشعر: أشقر أو أسود أو بني.
• البيانات الترتيبية المنفصلة: البيانات التي تتناسب مع شكل من أشكال النظام على مقياس. من الأمثلة على ذلك معرفة مدى رضاك ​​عن منتج أو خدمة على مقياس من واحد إلى خمسة.

يعد تحليل الانحدار اللوجستي مفيدًا للتنبؤ باحتمالية وقوع حدث ما. يساعد في تحديد الاحتمالات بين أي فئتين.

في الأساس ، يساعد الانحدار اللوجستي في حل مشاكل الاحتمالات والتصنيف . بمعنى آخر ، يمكنك توقع نتائج التصنيف والاحتمالية فقط من الانحدار اللوجستي.

على سبيل المثال ، يمكن استخدامه لتحديد احتمال أن يكون الشيء "صحيحًا أو خاطئًا" وأيضًا لتحديد نتيجتين مثل "نعم أو لا".

يمكن أن يساعد نموذج الانحدار اللوجستي أيضًا في تصنيف البيانات لعمليات الاستخراج والتحويل والتحميل (ETL). لا ينبغي استخدام الانحدار اللوجستي إذا كان عدد الملاحظات أقل من عدد الميزات. خلاف ذلك ، قد يؤدي ذلك إلى فرط التجهيز.

الانحدار الخطي مقابل الانحدار اللوجستي

بينما يتنبأ الانحدار اللوجستي بالمتغير الفئوي لواحد أو أكثر من المتغيرات المستقلة ،   الانحدارالخطي   يتوقع المتغير المستمر. بمعنى آخر ، يوفر الانحدار اللوجستي ناتجًا ثابتًا ، بينما يوفر الانحدار الخطي ناتجًا مستمرًا.

نظرًا لأن النتيجة مستمرة في الانحدار الخطي ، فهناك قيم محتملة لا نهائية للنتيجة. ولكن بالنسبة للانحدار اللوجستي ، فإن عدد قيم النتائج المحتملة محدود.

في الانحدار الخطي ، يجب أن تكون المتغيرات التابعة والمستقلة مرتبطة خطيًا. في حالة الانحدار اللوجستي ، يجب أن تكون المتغيرات المستقلة مرتبطة خطيًا بـ   احتمالات تسجيل   (تسجيل (ص / (1 - ع)).

بينما يتم تقدير الانحدار الخطي باستخدام طريقة المربعات الصغرى العادية ، يتم تقدير الانحدار اللوجستي باستخدام نهج تقدير الاحتمالية القصوى.

كلا الانحدار اللوجستي والخطي   التعلم الآلي الخاضع للإشراف   الخوارزميات والنوعين الرئيسيين لتحليل الانحدار. بينما يتم استخدام الانحدار اللوجستي لحل مشاكل التصنيف ، يستخدم الانحدار الخطي بشكل أساسي لمشاكل الانحدار.

بالعودة إلى مثال الوقت المستغرق في الدراسة ، يمكن أن يتنبأ الانحدار الخطي والانحدار اللوجستي بأشياء مختلفة. يمكن أن يساعد الانحدار اللوجستي في التنبؤ بما إذا كان الطالب قد اجتاز الاختبار أم لا. في المقابل ، يمكن أن يتنبأ الانحدار الخطي بدرجة الطالب.

افتراضات الانحدار اللوجستي

أثناء استخدام الانحدار اللوجستي ، نقوم ببعض الافتراضات. تعتبر الافتراضات جزءًا لا يتجزأ من الاستخدام الصحيح للانحدار اللوجستي لعمل التنبؤات وحل مشكلات التصنيف.

أنواع الانحدار اللوجستي

يمكن تقسيم الانحدار اللوجستي إلى أنواع مختلفة بناءً على عدد نتائج أو فئات المتغير التابع.

عندما نفكر في الانحدار اللوجستي ، فإننا على الأرجح نفكر في الانحدار اللوجستي الثنائي. في معظم أجزاء هذه المقالة ، عندما أشرنا إلى الانحدار اللوجستي ، كنا نشير إلى الانحدار اللوجستي الثنائي.

فيما يلي ثلاثة أنواع رئيسية من الانحدار اللوجستي.

الانحدار اللوجستي الثنائي

الانحدار اللوجستي الثنائي هو طريقة إحصائية تستخدم للتنبؤ بالعلاقة بين المتغير التابع والمتغير المستقل. في هذه الطريقة ، المتغير التابع هو متغير ثنائي ، مما يعني أنه يمكن أن يأخذ قيمتين فقط (نعم أو لا ، صواب أو خطأ ، نجاح أو فشل ، 0 أو 1).

مثال بسيط على الانحدار اللوجستي الثنائي هو تحديد ما إذا كان البريد الإلكتروني بريدًا عشوائيًا أم لا.

الانحدار اللوجستي متعدد الحدود

الانحدار اللوجستي متعدد الحدود هو امتداد للانحدار اللوجستي الثنائي. يسمح بأكثر من فئتين من النتيجة أو المتغير التابع.

إنه مشابه للانحدار اللوجستي الثنائي ولكن يمكن أن يكون له أكثر من نتيجتين محتملتين. هذا يعني أن متغير النتيجة يمكن أن يحتوي على ثلاثة أنواع غير مرتبة أو أكثر - أنواع ليس لها أهمية كمية. على سبيل المثال ، قد يمثل المتغير التابع "النوع أ" أو "النوع ب" أو "النوع ج".

على غرار الانحدار اللوجستي الثنائي ، يستخدم الانحدار اللوجستي متعدد الحدود أيضًا أقصى تقدير للاحتمالية لتحديد الاحتمال.

على سبيل المثال ، يمكن استخدام الانحدار اللوجستي متعدد الحدود لدراسة العلاقة بين التعليم والخيارات المهنية. هنا ، ستكون الخيارات المهنية هي المتغير التابع الذي يتكون من فئات من المهن المختلفة.

الانحدار اللوجستي الترتيبي

الانحدار اللوجستي الترتيبي ، المعروف أيضًا باسم الانحدار الترتيبي ، هو امتداد آخر للانحدار اللوجستي الثنائي. يتم استخدامه للتنبؤ بالمتغير التابع بثلاثة أنواع مرتبة أو أكثر - أنواع لها أهمية كمية. على سبيل المثال ، قد يمثل المتغير التابع "لا أوافق بشدة" أو "لا أوافق" أو "أوافق" أو "أوافق بشدة".

يمكن استخدامه لتحديد الأداء الوظيفي (ضعيف أو متوسط ​​أو ممتاز) والرضا الوظيفي (غير راضٍ أو راضٍ أو راضٍ للغاية).

مزايا وعيوب الانحدار اللوجستي

تنطبق العديد من مزايا وعيوب نموذج الانحدار اللوجستي على نموذج الانحدار الخطي. تتمثل إحدى أهم مزايا نموذج الانحدار اللوجستي في أنه لا يصنف فحسب ، بل يعطي أيضًا احتمالات.

ومع ذلك ، هناك عيوب عديدة للانحدار اللوجستي. إذا كانت هناك ميزة تفصل بين فئتين تمامًا ، فلا يمكن تدريب النموذج بعد الآن. هذا يسمى الفصل الكامل .

يحدث هذا بشكل أساسي لأن الوزن لهذه الميزة لن يتقارب لأن الوزن الأمثل سيكون لانهائيًا. ومع ذلك ، في معظم الحالات ، يمكن حل الفصل الكامل من خلال تحديد توزيع احتمالي مسبق للأوزان أو إدخال عقوبات على الأوزان.

عندما تمنحك الحياة خيارات ، فكر في الانحدار اللوجستي

قد يجادل الكثير بأن البشر لا يعيشون في عالم ثنائي ، على عكس أجهزة الكمبيوتر. بالطبع ، إذا أعطيت شريحة بيتزا وهامبرغر ، فيمكنك تناول قضمة من الاثنين دون الحاجة إلى اختيار واحدة فقط. ولكن إذا ألقيت نظرة فاحصة عليها ، فسيتم نقش قرار ثنائي على كل شيء (حرفيًا). يمكنك إما أن تأكل أو لا تأكل بيتزا ؛ ليس هناك حل وسط.

قد يكون تقييم أداء النموذج التنبئي معقدًا إذا كان هناك كمية محدودة من البيانات. لهذا ، يمكنك استخدام تقنية تسمى التحقق المتبادل ، والتي تتضمن تقسيم البيانات المتاحة إلى مجموعة تدريب ومجموعة اختبار.