Ce este regresia logistică? Învață când să-l folosești
Publicat: 2021-07-29Viața este plină de alegeri binare grele.
Ar trebui să am felia aia de pizza sau nu? Ar trebui să port o umbrelă sau nu?
În timp ce unele decizii pot fi luate pe bună dreptate cântărind argumentele pro și contra – de exemplu, este mai bine să nu mănânci o felie de pizza deoarece conține calorii suplimentare – unele decizii pot să nu fie atât de ușoare.
De exemplu, nu poți fi niciodată pe deplin sigur dacă va ploua sau nu într-o anumită zi. Deci decizia de a purta sau nu o umbrelă este una greu de luat.
Pentru a face alegerea corectă, este nevoie de capacități predictive. Această abilitate este foarte profitabilă și are numeroase aplicații în lumea reală, în special în computere. Calculatoarele iubesc deciziile binare. La urma urmei, ei vorbesc în cod binar.
Învățare automată algoritmii, mai precis algoritmul de regresie logistică , pot ajuta la prezicerea probabilității evenimentelor analizând punctele de date istorice. De exemplu, poate prezice dacă o persoană va câștiga alegerile sau dacă va ploua astăzi.
Ce este regresia logistică?
Regresia logistică este o metodă statistică utilizată pentru a prezice rezultatul unei variabile dependente pe baza observațiilor anterioare. Este un tip de analiză de regresie și este un algoritm utilizat în mod obișnuit pentru rezolvarea problemelor de clasificare binară.
Dacă vă întrebați ce este analiza de regresie , este un tip de tehnică de modelare predictivă folosită pentru a găsi relația dintre o variabilă dependentă și una sau mai multe variabile independente.
Un exemplu de variabile independente este timpul petrecut studiind și timpul petrecut pe Instagram. În acest caz, notele vor fi variabila dependentă. Acest lucru se datorează faptului că atât „timpul petrecut la studii”, cât și „timpul petrecut pe Instagram” ar influența notele; unul pozitiv iar celălalt negativ.
Regresia logistică este un algoritm de clasificare care prezice un rezultat binar bazat pe o serie de variabile independente. În exemplul de mai sus, aceasta ar însemna să preziceți dacă veți promova sau nu o clasă. Desigur, regresia logistică poate fi folosită și pentru a rezolva probleme de regresie, dar este folosită în principal pentru probleme de clasificare.
Sfat: utilizați software-ul de învățare automată pentru a automatiza sarcini monotone și pentru a lua decizii bazate pe date.
Un alt exemplu ar fi prezicerea dacă un student va fi acceptat într-o universitate. Pentru aceasta, vor fi luați în considerare mai mulți factori, cum ar fi scorul SAT, media punctuală a elevului și numărul de activități extracurriculare. Folosind date istorice despre rezultatele anterioare, algoritmul de regresie logistică va sorta elevii în categorii de „acceptare” sau „respingere”.
Regresia logistică este denumită și regresie logistică binomială sau regresie logistică binară. Dacă există mai mult de două clase de variabilă răspuns, se numește regresie logistică multinomială . Deloc surprinzător, regresia logistică a fost împrumutată din statistici și este unul dintre cei mai comuni algoritmi de clasificare binară din învățarea automată și știința datelor.
Știați? O reprezentare a unei rețele neuronale artificiale (ANN) poate fi văzută ca stivuind împreună un număr mare de clasificatori de regresie logistică.
Regresia logistică funcționează prin măsurarea relației dintre variabila dependentă (ceea ce dorim să prezicem) și una sau mai multe variabile independente (trăsăturile). Face acest lucru prin estimarea probabilităților cu ajutorul funcției sale logistice subiacente.
Termeni cheie în regresia logistică
Înțelegerea terminologiei este crucială pentru a descifra corect rezultatele regresiei logistice. Știind ce înseamnă anumiți termeni vă va ajuta să învățați rapid dacă sunteți nou în statistici sau învățare automată.
- Variabilă: orice număr, caracteristică sau cantitate care poate fi măsurată sau numărată. Vârsta, viteza, sexul și venitul sunt exemple.
- Coeficient: un număr, de obicei un întreg, înmulțit cu variabila pe care o însoțește. De exemplu, în 12y, numărul 12 este coeficientul.
- EXP: formă scurtă de exponențial.
- Valori abere: puncte de date care diferă semnificativ de restul.
- Estimator: un algoritm sau o formulă care generează estimări ale parametrilor.
- Testul chi-pătrat: Denumit și testul chi-pătrat, este o metodă de testare a ipotezelor pentru a verifica dacă datele sunt conform așteptărilor.
- Eroare standard: abaterea standard aproximativă a unei populații eșantion statistice.
- Regularizare: O metodă utilizată pentru reducerea erorii și supraadaptarea prin ajustarea unei funcții (în mod corespunzător) pe setul de date de antrenament.
- Multicolinearitate: Apariția intercorelațiilor între două sau mai multe variabile independente.
- Bunătatea potrivirii: descrierea cât de bine se potrivește un model statistic unui set de observații.
- Odds ratio: Măsura puterii asocierii dintre două evenimente.
- Funcții de log-probabilitate: evaluează bunătatea de potrivire a unui model statistic.
- Testul Hosmer–Lemeshow: un test care evaluează dacă ratele de evenimente observate se potrivesc cu ratele de evenimente așteptate.
Ce este o funcție logistică?
Regresia logistică este numită după funcția folosită în centrul său, funcția logistică . Statisticienii l-au folosit inițial pentru a descrie proprietățile creșterii populației. Funcția sigmoidă și funcția logit sunt câteva variații ale funcției logistice. Funcția Logit este inversul funcției logistice standard.
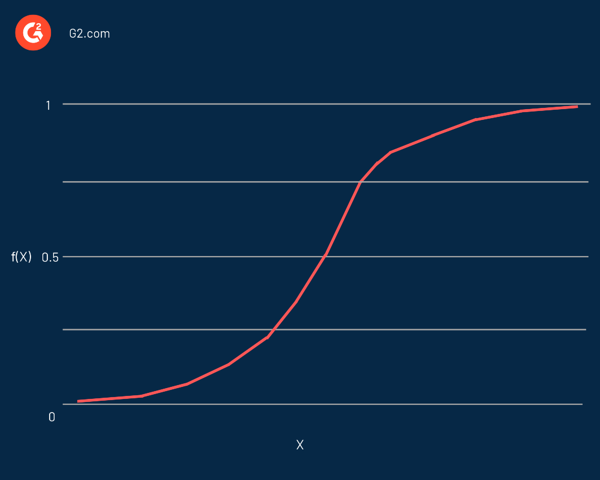
De fapt, este o curbă în formă de S capabilă să ia orice număr real și să-l mapeze într-o valoare între 0 și 1, dar niciodată exact la acele limite. Este reprezentat de ecuația:
f(x) = L / 1 + e^-k(x - x0)
În această ecuație:
- f(X) este rezultatul funcției
- L este valoarea maximă a curbei
- e este baza logaritmilor naturali
- k este abruptul curbei
- x este numărul real
- x0 este valorile x ale punctului de mijloc sigmoid
Dacă valoarea prezisă este o valoare negativă considerabilă, este considerată aproape de zero. Pe de altă parte, dacă valoarea prezisă este o valoare pozitivă semnificativă, este considerată aproape de una.
Regresia logistică este reprezentată similar cu modul în care este definită regresia liniară folosind ecuația unei linii drepte. O diferență notabilă față de regresia liniară este că rezultatul va fi o valoare binară (0 sau 1) mai degrabă decât o valoare numerică.
Iată un exemplu de ecuație de regresie logistică:
y = e^(b0 + b1*x) / (1 + e^(b0 + b1*x))
În această ecuație:
- y este valoarea prezisă (sau rezultatul)
- b0 este părtinirea (sau termenul de interceptare)
- b1 este coeficientul pentru intrare
- x este variabila predictor (sau intrarea)
Variabila dependentă urmează în general distribuția Bernoulli. Valorile coeficienților sunt estimate utilizând estimarea cu probabilitatea maximă (MLE) , coborârea gradientului și coborârea gradientului stocastic .
Ca și în cazul altor algoritmi de clasificare precum k-cei mai apropiati vecini, a matricea de confuzie este utilizat pentru a evalua acuratețea algoritmului de regresie logistică.
Știați? Regresia logistică face parte dintr-o familie mai mare de modele liniare generalizate (GLM).
La fel ca și evaluarea performanței unui clasificator, este la fel de important să știm de ce modelul a clasificat o observație într-un anumit mod. Cu alte cuvinte, avem nevoie ca decizia clasificatorului să fie interpretabilă.
Deși interpretabilitatea nu este ușor de definit, intenția sa principală este ca oamenii să știe de ce un algoritm a luat o anumită decizie. În cazul regresiei logistice, aceasta poate fi combinată cu teste statistice precum Testul Wald sau testul raportului de probabilitate pentru interpretabilitate.
Când să folosiți regresia logistică
Regresia logistică este aplicată pentru a prezice variabila dependentă categorială. Cu alte cuvinte, este folosit atunci când predicția este categorică, de exemplu, da sau nu, adevărat sau fals, 0 sau 1. Probabilitatea prezisă sau rezultatul regresiei logistice poate fi oricare dintre ele și nu există cale de mijloc.
În cazul variabilelor predictoare, acestea pot face parte din oricare dintre următoarele categorii:
- Date continue: date care pot fi măsurate pe o scară infinită. Poate lua orice valoare între două numere. Exemple sunt greutatea în lire sau temperatura în Fahrenheit.
- Date nominale discrete: date care se încadrează în categorii denumite. Un exemplu rapid este culoarea părului: blond, negru sau maro.
- Date discrete, ordinale: date care se încadrează într-o anumită formă de ordine pe o scară. Un exemplu este să spuneți cât de mulțumit sunteți de un produs sau serviciu pe o scară de la unu la cinci.
Analiza regresiei logistice este valoroasă pentru a prezice probabilitatea unui eveniment. Ajută la determinarea probabilităților dintre oricare două clase.

Pe scurt, analizând datele istorice, regresia logistică poate prezice dacă:
- Un e-mail este un spam
- Azi va ploua
- O tumoare este fatală
- O persoană va cumpăra o mașină
- O tranzacție online este frauduloasă
- Un concurent va câștiga alegerile
- Un grup de utilizatori va cumpăra un produs
- Un titular de poliță de asigurare va expira înainte de expirarea termenului poliței
- Un destinatar de e-mail promoțional este un răspuns sau care nu răspunde
În esență, regresia logistică ajută la rezolvarea problemelor de probabilitate și clasificare . Cu alte cuvinte, vă puteți aștepta doar la rezultate de clasificare și probabilitate din regresia logistică.
De exemplu, poate fi folosit pentru a determina probabilitatea ca ceva să fie „adevărat sau fals” și, de asemenea, pentru a decide între două rezultate precum „da sau nu”.
Un model de regresie logistică poate ajuta, de asemenea, la clasificarea datelor pentru operațiunile de extragere, transformare și încărcare (ETL). Regresia logistică nu ar trebui utilizată dacă numărul de observații este mai mic decât numărul de caracteristici. În caz contrar, poate duce la supraadaptare.
Regresia liniară vs. regresia logistică
În timp ce regresia logistică prezice variabila categorială pentru una sau mai multe variabile independente, regresie liniara prezice variabila continuă. Cu alte cuvinte, regresia logistică oferă o ieșire constantă, în timp ce regresia liniară oferă o ieșire continuă.
Deoarece rezultatul este continuu în regresie liniară, există infinite valori posibile pentru rezultat. Dar pentru regresia logistică, numărul de valori posibile de rezultat este limitat.
În regresia liniară, variabilele dependente și independente ar trebui să fie legate liniar. În cazul regresiei logistice, variabilele independente ar trebui să fie liniar legate de log cote (log (p/(1-p)).
Sfat: Regresia logistică poate fi implementată în orice limbaj de programare utilizat pentru analiza datelor, cum ar fi R, Python, Java și MATLAB.
În timp ce regresia liniară este estimată folosind metoda celor mai mici pătrate obișnuite, regresia logistică este estimată utilizând abordarea estimării cu probabilitatea maximă.
Atât regresia logistică, cât și regresia liniară sunt învățare automată supravegheată algoritmi și cele două tipuri principale de analiză de regresie. În timp ce regresia logistică este folosită pentru a rezolva probleme de clasificare, regresia liniară este folosită în primul rând pentru problemele de regresie.
Revenind la exemplul timpului petrecut studiind, regresia liniară și regresia logistică pot prezice lucruri diferite. Regresia logistică poate ajuta să prezică dacă studentul a promovat sau nu un examen. În schimb, regresia liniară poate prezice scorul elevului.
Ipoteze de regresie logistică
În timp ce folosim regresia logistică, facem câteva ipoteze. Ipotezele sunt integrante pentru utilizarea corectă a regresiei logistice pentru a face predicții și a rezolva probleme de clasificare.
Următoarele sunt principalele ipoteze ale regresiei logistice:
- Există puțină sau deloc multicoliniaritate între variabilele independente.
- Variabilele independente sunt legate liniar de cotele log (log (p/(1-p)).
- Variabila dependentă este dihotomică sau binară ; se încadrează în două categorii distincte. Acest lucru se aplică numai regresiei logistice binare, despre care se discută mai târziu.
- Nu există variabile fără sens, deoarece acestea pot duce la erori.
- Dimensiunile eșantionului de date sunt mai mari , ceea ce este integral pentru rezultate mai bune.
- Nu există valori aberante .
Tipuri de regresie logistică
Regresia logistică poate fi împărțită în diferite tipuri în funcție de numărul de rezultate sau categorii ale variabilei dependente.
Când ne gândim la regresia logistică, cel mai probabil ne gândim la regresia logistică binară. În majoritatea părților acestui articol, când ne-am referit la regresia logistică, ne referim la regresia logistică binară.
Următoarele sunt cele trei tipuri principale de regresie logistică.
Regresie logistică binară
Regresia logistică binară este o metodă statistică utilizată pentru a prezice relația dintre o variabilă dependentă și o variabilă independentă. În această metodă, variabila dependentă este o variabilă binară, adică poate lua doar două valori (da sau nu, adevărat sau fals, succes sau eșec, 0 sau 1).
Un exemplu simplu de regresie logistică binară este determinarea dacă un e-mail este spam sau nu.
Regresie logistică multinomială
Regresia logistică multinomială este o extensie a regresiei logistice binare. Permite mai mult de două categorii de rezultat sau variabilă dependentă.
Este similar cu regresia logistică binară, dar poate avea mai mult de două rezultate posibile. Aceasta înseamnă că variabila rezultat poate avea trei sau mai multe tipuri posibile neordonate – tipuri fără semnificație cantitativă. De exemplu, variabila dependentă poate reprezenta „Tipul A”, „Tipul B” sau „Tipul C”.
Similar cu regresia logistică binară, regresia logistică multinomială utilizează, de asemenea, estimarea probabilității maxime pentru a determina probabilitatea.
De exemplu, regresia logistică multinomială poate fi utilizată pentru a studia relația dintre educația cuiva și alegerile ocupaționale. Aici, alegerile ocupaționale vor fi variabila dependentă care constă din categorii de diferite ocupații.
Regresia logistică ordinală
Regresia logistică ordinală, cunoscută și sub numele de regresie ordinală, este o altă extensie a regresiei logistice binare. Este folosit pentru a prezice variabila dependentă cu trei sau mai multe tipuri ordonate posibile - tipuri având semnificație cantitativă. De exemplu, variabila dependentă poate reprezenta „Sunt de acord”, „Nu sunt de acord”, „De acord” sau „Sunt de acord”.
Poate fi folosit pentru a determina performanța la locul de muncă (slab, mediu sau excelent) și satisfacția în muncă (nesatisfăcut, mulțumit sau foarte mulțumit).
Avantajele și dezavantajele regresiei logistice
Multe dintre avantajele și dezavantajele modelului de regresie logistică se aplică modelului de regresie liniară. Unul dintre cele mai semnificative avantaje ale modelului de regresie logistică este că nu doar clasifică, ci oferă și probabilități.
Următoarele sunt câteva dintre avantajele algoritmului de regresie logistică.
- Simplu de înțeles, ușor de implementat și eficient de antrenat
- Funcționează bine atunci când setul de date este separabil liniar
- Precizie bună pentru seturi de date mai mici
- Nu face nicio presupunere cu privire la distribuția claselor
- Oferă direcția de asociere (pozitivă sau negativă)
- Util pentru a găsi relații între caracteristici
- Oferă probabilități bine calibrate
- Mai puțin predispus la supraadaptare în seturile de date cu dimensiuni reduse
- Poate fi extins la clasificarea multiclasă
Cu toate acestea, există numeroase dezavantaje ale regresiei logistice. Dacă există o caracteristică care ar separa perfect două clase, atunci modelul nu mai poate fi antrenat. Aceasta se numește separare completă .
Acest lucru se întâmplă în principal pentru că greutatea pentru acea caracteristică nu ar converge, deoarece greutatea optimă ar fi infinită. Cu toate acestea, în majoritatea cazurilor, separarea completă poate fi rezolvată prin definirea unei distribuții de probabilitate prealabile a ponderilor sau introducerea penalizării ponderilor.
Următoarele sunt câteva dintre dezavantajele algoritmului de regresie logistică:
- Construiește limite liniare
- Poate duce la supraadaptare dacă numărul de caracteristici este mai mare decât numărul de observații
- Predictorii ar trebui să aibă multicoliniaritate medie sau deloc
- O provocare pentru a obține relații complexe. Algoritmii precum rețelele neuronale sunt mai potriviți și mai puternici
- Poate fi folosit doar pentru a prezice funcții discrete
- Nu pot rezolva probleme neliniare
- Sensibilă la valori aberante
Când viața îți oferă opțiuni, gândește-te la regresia logistică
Mulți ar putea argumenta că oamenii nu trăiesc într-o lume binară, spre deosebire de computere. Desigur, dacă vi se oferă o felie de pizza și un hamburger, puteți mânca din ambele fără a fi nevoie să alegeți doar una. Dar dacă te uiți mai atent la asta, o decizie binară este gravată (la propriu) totul. Poți alege să mănânci sau să nu mănânci o pizza; nu există cale de mijloc.
Evaluarea performanței unui model predictiv poate fi dificilă dacă există o cantitate limitată de date. Pentru aceasta, puteți utiliza o tehnică numită validare încrucișată, care implică partiționarea datelor disponibile într-un set de antrenament și un set de testare.
