Was ist logistische Regression? Erfahren Sie, wann Sie es verwenden

Das Leben ist voller harter binärer Entscheidungen.

Soll ich das Stück Pizza haben oder nicht? Soll ich einen Regenschirm mitnehmen oder nicht?

Während einige Entscheidungen durch Abwägen der Vor- und Nachteile richtig getroffen werden können – zum Beispiel ist es besser, ein Stück Pizza nicht zu essen, da es zusätzliche Kalorien enthält – sind einige Entscheidungen möglicherweise nicht so einfach.

Man kann zum Beispiel nie ganz sicher sein, ob es an einem bestimmten Tag regnen wird oder nicht. Die Entscheidung, ob man einen Regenschirm dabei hat oder nicht, ist also schwer zu treffen.

Um die richtige Wahl zu treffen, benötigt man Vorhersagefähigkeiten. Diese Fähigkeit ist sehr lukrativ und hat zahlreiche Anwendungen in der realen Welt, insbesondere in Computern. Computer lieben binäre Entscheidungen. Schließlich sprechen sie im Binärcode.

Maschinelles Lernen   Algorithmen, genauer gesagt der logistische Regressionsalgorithmus , können helfen, die Wahrscheinlichkeit von Ereignissen vorherzusagen, indem sie historische Datenpunkte betrachten. Es kann zum Beispiel vorhersagen, ob eine Person die Wahl gewinnt oder ob es heute regnen wird.

Wenn Sie sich fragen, was eine Regressionsanalyse ist, handelt es sich um eine Art prädiktive Modellierungstechnik, die verwendet wird, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu finden.

Ein Beispiel für unabhängige Variablen ist die Lernzeit und die auf Instagram verbrachte Zeit. In diesem Fall sind Noten die abhängige Variable. Denn sowohl die „Lernzeit“ als auch die „Auf Instagram verbrachte Zeit“ würden die Noten beeinflussen; das eine positiv und das andere negativ.

Die logistische Regression ist ein Klassifizierungsalgorithmus , der ein binäres Ergebnis basierend auf einer Reihe unabhängiger Variablen vorhersagt. Im obigen Beispiel würde dies bedeuten, vorherzusagen, ob Sie eine Klasse bestehen oder nicht bestehen würden. Natürlich kann die logistische Regression auch zur Lösung von Regressionsproblemen verwendet werden, aber sie wird hauptsächlich für Klassifizierungsprobleme verwendet.

Ein weiteres Beispiel wäre die Vorhersage, ob ein Student an einer Universität angenommen wird. Dazu werden mehrere Faktoren wie die SAT-Punktzahl, der Notendurchschnitt der Schüler und die Anzahl der außerschulischen Aktivitäten berücksichtigt. Unter Verwendung historischer Daten über frühere Ergebnisse sortiert der logistische Regressionsalgorithmus die Schüler in die Kategorien „Akzeptieren“ oder „Ablehnen“.

Die logistische Regression wird auch als binomiale logistische Regression oder binäre logistische Regression bezeichnet. Wenn es mehr als zwei Klassen der Antwortvariablen gibt, spricht man von multinomialer logistischer Regression . Es überrascht nicht, dass die logistische Regression aus der Statistik entlehnt wurde und einer der häufigsten binären Klassifizierungsalgorithmen im maschinellen Lernen und in der Datenwissenschaft ist.

Die logistische Regression misst die Beziehung zwischen der abhängigen Variablen (was wir vorhersagen möchten) und einer oder mehreren unabhängigen Variablen (den Merkmalen). Es tut dies, indem es die Wahrscheinlichkeiten mit Hilfe seiner zugrunde liegenden logistischen Funktion schätzt.

Schlüsselbegriffe der logistischen Regression

Das Verständnis der Terminologie ist entscheidend, um die Ergebnisse der logistischen Regression richtig zu entschlüsseln. Wenn Sie wissen, was bestimmte Begriffe bedeuten, können Sie schnell lernen, wenn Sie mit Statistik oder maschinellem Lernen noch nicht vertraut sind.

Was ist eine logistische Funktion?

Die logistische Regression ist nach der im Kern verwendeten Funktion benannt, der logistischen Funktion . Statistiker verwendeten es zunächst, um die Eigenschaften des Bevölkerungswachstums zu beschreiben. Sigmoidfunktion und Logitfunktion sind einige Variationen der logistischen Funktion. Die Logit-Funktion ist die Umkehrung der Standard-Logistikfunktion.

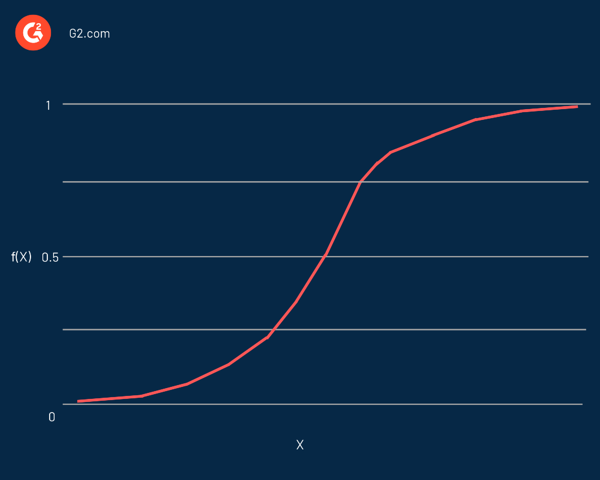
Tatsächlich ist es eine S-förmige Kurve, die in der Lage ist, jede reelle Zahl zu nehmen und sie in einen Wert zwischen 0 und 1 abzubilden, aber niemals genau an diesen Grenzen. Es wird durch die Gleichung dargestellt:

In dieser Gleichung:

• f(X) ist die Ausgabe der Funktion
• L ist der Maximalwert der Kurve
• e ist die Basis der natürlichen Logarithmen
• k ist die Steilheit der Kurve
• x ist die reelle Zahl
• x0 sind die x-Werte des Sigmoid-Mittelpunkts

Wenn der vorhergesagte Wert ein beträchtlicher negativer Wert ist, wird er als nahe Null betrachtet. Wenn der vorhergesagte Wert andererseits ein signifikant positiver Wert ist, wird er als nahe eins betrachtet.

Die logistische Regression wird ähnlich dargestellt, wie die lineare Regression unter Verwendung der Gleichung einer geraden Linie definiert wird. Ein bemerkenswerter Unterschied zur linearen Regression besteht darin, dass die Ausgabe ein binärer Wert (0 oder 1) und kein numerischer Wert ist.

Hier ist ein Beispiel für eine logistische Regressionsgleichung:

In dieser Gleichung:

• y ist der vorhergesagte Wert (oder die Ausgabe)
• b0 ist die Vorspannung (oder der Intercept-Term)
• b1 ist der Koeffizient für die Eingabe
• x ist die Prädiktorvariable (oder die Eingabe)

Die abhängige Variable folgt im Allgemeinen dem   Bernoulli-Verteilung. Die Werte der Koeffizienten werden unter Verwendung von Maximum-Likelihood-Schätzung (MLE) , Gradientenabstieg und stochastischem Gradientenabstieg geschätzt.

Wie bei anderen Klassifizierungsalgorithmen wie dem   k-nächste Nachbarn, a   Verwirrung Matrix   wird verwendet, um die Genauigkeit des logistischen Regressionsalgorithmus zu bewerten.

Genau wie bei der Bewertung der Leistung eines Klassifikators ist es ebenso wichtig zu wissen, warum das Modell eine Beobachtung auf eine bestimmte Weise klassifiziert hat. Mit anderen Worten, wir brauchen die Entscheidung des Klassifikators, um interpretierbar zu sein.

Obwohl die Interpretierbarkeit nicht einfach zu definieren ist, besteht ihre Hauptabsicht darin, dass Menschen wissen sollten, warum ein Algorithmus eine bestimmte Entscheidung getroffen hat. Im Fall der logistischen Regression kann sie mit statistischen Tests wie der kombiniert werden   Wald-Test   oder der   Wahrscheinlichkeitsverhältnis-Test   für Interpretierbarkeit.

Wann ist die logistische Regression zu verwenden?

Die logistische Regression wird angewendet, um die kategoriale abhängige Variable vorherzusagen. Mit anderen Worten, es wird verwendet, wenn die Vorhersage kategorisch ist, z. B. ja oder nein, wahr oder falsch, 0 oder 1. Die vorhergesagte Wahrscheinlichkeit oder Ausgabe der logistischen Regression kann eine von beiden sein, und es gibt keinen Mittelweg.

Im Fall von Prädiktorvariablen können sie Teil einer der folgenden Kategorien sein:

• Kontinuierliche Daten: Daten, die auf einer unendlichen Skala gemessen werden können. Es kann jeden Wert zwischen zwei Zahlen annehmen. Beispiele sind das Gewicht in Pfund oder die Temperatur in Fahrenheit.
• Diskrete Nominaldaten: Daten, die in benannte Kategorien passen. Ein kurzes Beispiel ist die Haarfarbe: blond, schwarz oder braun.
• Diskrete, ordinale Daten: Daten, die in eine Art Ordnung auf einer Skala passen. Ein Beispiel ist die Angabe, wie zufrieden Sie mit einem Produkt oder einer Dienstleistung auf einer Skala von eins bis fünf sind.

Die logistische Regressionsanalyse ist wertvoll, um die Wahrscheinlichkeit eines Ereignisses vorherzusagen. Es hilft, die Wahrscheinlichkeiten zwischen zwei beliebigen Klassen zu bestimmen.

Im Wesentlichen hilft die logistische Regression bei der Lösung von Wahrscheinlichkeits- und Klassifizierungsproblemen . Mit anderen Worten, Sie können von der logistischen Regression nur Klassifizierungs- und Wahrscheinlichkeitsergebnisse erwarten.

Beispielsweise kann es verwendet werden, um die Wahrscheinlichkeit zu bestimmen, dass etwas „wahr oder falsch“ ist, und auch um zwischen zwei Ergebnissen wie „ja oder nein“ zu entscheiden.

Ein logistisches Regressionsmodell kann auch dabei helfen, Daten für Extraktions-, Transformations- und Ladevorgänge (ETL) zu klassifizieren. Die logistische Regression sollte nicht verwendet werden, wenn die Anzahl der Beobachtungen geringer ist als die Anzahl der Features. Andernfalls kann es zu einer Überanpassung kommen.

Lineare Regression vs. logistische Regression

Während die logistische Regression die kategoriale Variable für eine oder mehrere unabhängige Variablen vorhersagt,   lineare Regression   sagt die kontinuierliche Variable voraus. Mit anderen Worten, die logistische Regression liefert eine konstante Ausgabe, während die lineare Regression eine kontinuierliche Ausgabe liefert.

Da das Ergebnis bei der linearen Regression stetig ist, gibt es unendlich viele mögliche Werte für das Ergebnis. Aber für die logistische Regression ist die Anzahl der möglichen Ergebniswerte begrenzt.

Bei der linearen Regression sollten die abhängigen und unabhängigen Variablen linear zusammenhängen. Im Fall der logistischen Regression sollten die unabhängigen Variablen linear mit der verknüpft sein   Quoten loggen   (log (p/(1-p)).

Während die lineare Regression mit der gewöhnlichen Methode der kleinsten Quadrate geschätzt wird, wird die logistische Regression mit dem Ansatz der Maximum-Likelihood-Schätzung geschätzt.

Sowohl die logistische als auch die lineare Regression sind   überwachtes maschinelles Lernen   Algorithmen und die beiden Hauptarten der Regressionsanalyse. Während die logistische Regression zur Lösung von Klassifikationsproblemen verwendet wird, wird die lineare Regression hauptsächlich für Regressionsprobleme verwendet.

Um auf das Beispiel der Lernzeit zurückzukommen, können lineare Regression und logistische Regression verschiedene Dinge vorhersagen. Die logistische Regression kann dabei helfen, vorherzusagen, ob der Student eine Prüfung bestanden hat oder nicht. Im Gegensatz dazu kann die lineare Regression die Punktzahl des Schülers vorhersagen.

Annahmen zur logistischen Regression

Bei der Verwendung der logistischen Regression treffen wir einige Annahmen. Annahmen sind wesentlich, um die logistische Regression korrekt zu verwenden, um Vorhersagen zu treffen und Klassifizierungsprobleme zu lösen.

Arten der logistischen Regression

Die logistische Regression kann basierend auf der Anzahl der Ergebnisse oder Kategorien der abhängigen Variablen in verschiedene Typen unterteilt werden.

Wenn wir an logistische Regression denken, denken wir höchstwahrscheinlich an binäre logistische Regression. Wenn wir uns in den meisten Teilen dieses Artikels auf die logistische Regression bezogen, haben wir uns auf die binäre logistische Regression bezogen.

Im Folgenden sind die drei Haupttypen der logistischen Regression aufgeführt.

Binäre logistische Regression

Die binäre logistische Regression ist eine statistische Methode zur Vorhersage der Beziehung zwischen einer abhängigen Variablen und einer unabhängigen Variablen. Bei dieser Methode ist die abhängige Variable eine binäre Variable, was bedeutet, dass sie nur zwei Werte annehmen kann (ja oder nein, wahr oder falsch, Erfolg oder Misserfolg, 0 oder 1).

Ein einfaches Beispiel für eine binäre logistische Regression ist die Bestimmung, ob eine E-Mail Spam ist oder nicht.

Multinomiale logistische Regression

Die multinomiale logistische Regression ist eine Erweiterung der binären logistischen Regression. Es erlaubt mehr als zwei Kategorien des Ergebnisses oder der abhängigen Variablen.

Sie ähnelt der binären logistischen Regression, kann aber mehr als zwei mögliche Ergebnisse haben. Das bedeutet, dass die Ergebnisvariable drei oder mehr mögliche ungeordnete Typen haben kann – Typen ohne quantitative Bedeutung. Beispielsweise kann die abhängige Variable "Typ A", "Typ B" oder "Typ C" darstellen.

Ähnlich wie bei der binären logistischen Regression verwendet auch die multinomiale logistische Regression eine Maximum-Likelihood-Schätzung, um die Wahrscheinlichkeit zu bestimmen.

Beispielsweise kann die multinomiale logistische Regression verwendet werden, um die Beziehung zwischen der eigenen Ausbildung und der Berufswahl zu untersuchen. Hier wird die Berufswahl die abhängige Variable sein, die sich aus Kategorien verschiedener Berufe zusammensetzt.

Ordinale logistische Regression

Die ordinale logistische Regression , auch ordinale Regression genannt, ist eine weitere Erweiterung der binären logistischen Regression. Es wird verwendet, um die abhängige Variable mit drei oder mehr möglichen geordneten Typen vorherzusagen – Typen mit quantitativer Bedeutung. Beispielsweise kann die abhängige Variable „Stimme überhaupt nicht zu“, „Stimme nicht zu“, „Stimme zu“ oder „Stimme voll und ganz zu“ darstellen.

Es kann verwendet werden, um die Arbeitsleistung (schlecht, durchschnittlich oder ausgezeichnet) und die Arbeitszufriedenheit (unzufrieden, zufrieden oder sehr zufrieden) zu bestimmen.

Vor- und Nachteile der logistischen Regression

Viele der Vor- und Nachteile des logistischen Regressionsmodells gelten auch für das lineare Regressionsmodell. Einer der wichtigsten Vorteile des logistischen Regressionsmodells besteht darin, dass es nicht nur klassifiziert, sondern auch Wahrscheinlichkeiten angibt.

Die logistische Regression hat jedoch zahlreiche Nachteile. Wenn es eine Funktion gibt, die zwei Klassen perfekt trennen würde, kann das Modell nicht mehr trainiert werden. Dies wird als vollständige Trennung bezeichnet.

Dies geschieht hauptsächlich, weil die Gewichtung für dieses Merkmal nicht konvergieren würde, da die optimale Gewichtung unendlich wäre. In den meisten Fällen kann jedoch eine vollständige Trennung gelöst werden, indem eine vorherige Wahrscheinlichkeitsverteilung von Gewichten definiert oder eine Bestrafung der Gewichte eingeführt wird.

Wenn das Leben Ihnen Optionen bietet, denken Sie an eine logistische Regression

Viele mögen argumentieren, dass Menschen im Gegensatz zu Computern nicht in einer binären Welt leben. Wenn Sie ein Stück Pizza und einen Hamburger bekommen, können Sie natürlich beides beißen, ohne sich nur für eines entscheiden zu müssen. Aber wenn man genauer hinschaut, ist (buchstäblich) allem eine binäre Entscheidung eingraviert. Sie können entweder eine Pizza essen oder nicht essen; es gibt keinen Mittelweg.

Die Bewertung der Leistung eines Vorhersagemodells kann schwierig sein, wenn nur eine begrenzte Datenmenge vorhanden ist. Dazu können Sie eine Technik namens Kreuzvalidierung verwenden, bei der die verfügbaren Daten in eine Trainingsmenge und eine Testmenge aufgeteilt werden.