Что такое логистическая регрессия? Узнайте, когда его использовать

Жизнь полна сложных бинарных выборов.

Должен ли я есть этот кусок пиццы или нет? Должен ли я носить зонтик или нет?

Хотя некоторые решения можно принять правильно, взвесив все «за» и «против» — например, лучше не есть кусок пиццы, так как она содержит лишние калории, — некоторые решения могут быть не такими простыми.

Например, вы никогда не можете быть полностью уверены, будет ли дождь в конкретный день. Так что решить, брать с собой зонт или нет, сложно.

Чтобы сделать правильный выбор, нужны предсказательные способности. Эта способность очень прибыльна и имеет многочисленные приложения в реальном мире, особенно в компьютерах. Компьютеры любят бинарные решения. Ведь они говорят двоичным кодом.

Машинное обучение   Алгоритмы, точнее алгоритм логистической регрессии , могут помочь предсказать вероятность событий, просматривая исторические точки данных. Например, он может предсказать, победит ли человек на выборах или будет ли сегодня дождь.

Если вам интересно, что такое регрессионный анализ , то это тип метода прогнозного моделирования, используемый для поиска взаимосвязи между зависимой переменной и одной или несколькими независимыми переменными.

Примером независимых переменных является время, потраченное на учебу, и время, проведенное в Instagram. В этом случае оценки будут зависимой переменной. Это связано с тем, что как «время, потраченное на учебу», так и «время, проведенное в Instagram» будут влиять на оценки; один положительно, а другой отрицательно.

Логистическая регрессия — это алгоритм классификации, который предсказывает бинарный результат на основе ряда независимых переменных. В приведенном выше примере это означало бы предсказать, пройдете вы класс или нет. Конечно, логистическая регрессия также может использоваться для решения задач регрессии, но в основном она используется для задач классификации.

Другим примером может быть прогнозирование того, будет ли студент принят в университет. Для этого будут учитываться несколько факторов, таких как балл SAT, средний балл учащегося и количество внеклассных занятий. Используя исторические данные о предыдущих результатах, алгоритм логистической регрессии сортирует учащихся по категориям «принято» или «отказано».

Логистическую регрессию также называют биномиальной логистической регрессией или бинарной логистической регрессией. Если существует более двух классов переменной ответа, это называется полиномиальной логистической регрессией . Неудивительно, что логистическая регрессия была заимствована из статистики и является одним из наиболее распространенных алгоритмов бинарной классификации в машинном обучении и науке о данных.

Логистическая регрессия работает путем измерения отношения между зависимой переменной (то, что мы хотим предсказать) и одной или несколькими независимыми переменными (функциями). Он делает это, оценивая вероятности с помощью лежащей в его основе логистической функции.

Ключевые термины логистической регрессии

Понимание терминологии имеет решающее значение для правильной расшифровки результатов логистической регрессии. Знание того, что означают конкретные термины, поможет вам быстро научиться, если вы новичок в статистике или машинном обучении.

Что такое логистическая функция?

Логистическая регрессия названа в честь функции, используемой в ее основе, логистической функции . Статистики первоначально использовали его для описания свойств роста населения. Сигмовидная функция и логит-функция являются некоторыми вариантами логистической функции. Логит-функция обратна стандартной логистической функции.

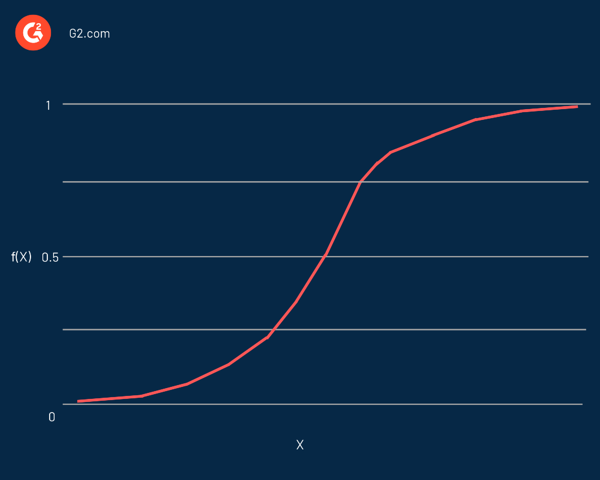
По сути, это S-образная кривая, способная брать любое действительное число и преобразовывать его в значение от 0 до 1, но никогда точно в этих пределах. Он представлен уравнением:

В этом уравнении:

• f(X) — результат функции
• L - максимальное значение кривой
• e - основание натуральных логарифмов
• k - крутизна кривой
• х это реальное число
• x0 - значения x средней точки сигмоиды

Если прогнозируемое значение является значительным отрицательным значением, оно считается близким к нулю. С другой стороны, если прогнозируемое значение является значительным положительным значением, оно считается близким к единице.

Логистическая регрессия представлена ​​​​подобно тому, как линейная регрессия определяется с помощью уравнения прямой линии. Заметное отличие от линейной регрессии заключается в том, что на выходе будет двоичное значение (0 или 1), а не числовое значение.

Вот пример уравнения логистической регрессии:

В этом уравнении:

• y - прогнозируемое значение (или результат)
• b0 - это смещение (или термин перехвата)
• b1 – коэффициент для входа
• x - переменная-предиктор (или вход)

Зависимая переменная обычно следует   Распределение Бернулли. Значения коэффициентов оцениваются с использованием оценки максимального правдоподобия (MLE) , градиентного спуска и стохастического градиентного спуска .

Как и в случае с другими алгоритмами классификации, такими как   k-ближайшие соседи, a   матрица путаницы   используется для оценки точности алгоритма логистической регрессии.

Точно так же, как при оценке производительности классификатора, не менее важно знать, почему модель классифицировала наблюдение определенным образом. Другими словами, нам нужно, чтобы решение классификатора можно было интерпретировать.

Хотя интерпретируемость определить непросто, ее основная цель состоит в том, чтобы люди знали, почему алгоритм принял то или иное решение. В случае логистической регрессии ее можно комбинировать со статистическими тестами, такими как   Тест Вальда   или   критерий отношения правдоподобия   для интерпретируемости.

Когда использовать логистическую регрессию

Логистическая регрессия применяется для прогнозирования категориальной зависимой переменной. Другими словами, он используется, когда прогноз носит категорический характер, например, да или нет, истина или ложь, 0 или 1. Прогнозируемая вероятность или результат логистической регрессии может быть любой из них, и среднего уровня нет.

В случае переменных-предикторов они могут быть частью любой из следующих категорий:

• Непрерывные данные: данные, которые можно измерить в бесконечном масштабе. Может принимать любое значение между двумя числами. Примерами являются вес в фунтах или температура в градусах Фаренгейта.
• Дискретные, номинальные данные: данные, которые соответствуют именованным категориям. Быстрый пример — цвет волос: светлые, черные или каштановые.
• Дискретные, порядковые данные: данные, которые соответствуют некоторому порядку на шкале. В качестве примера можно указать, насколько вы удовлетворены продуктом или услугой по шкале от одного до пяти.

Логистический регрессионный анализ ценен для прогнозирования вероятности события. Это помогает определить вероятности между любыми двумя классами.

По сути, логистическая регрессия помогает решить проблемы вероятности и классификации . Другими словами, вы можете ожидать от логистической регрессии только результаты классификации и вероятности.

Например, его можно использовать для определения вероятности того, что что-то будет «истинным или ложным», а также для выбора между двумя исходами, такими как «да» или «нет».

Модель логистической регрессии также может помочь классифицировать данные для операций извлечения, преобразования и загрузки (ETL). Логистическую регрессию не следует использовать, если количество наблюдений меньше количества признаков. В противном случае это может привести к переобучению.

Линейная регрессия против логистической регрессии

В то время как логистическая регрессия предсказывает категориальную переменную для одной или нескольких независимых переменных,   линейная регрессия   предсказывает непрерывную переменную. Другими словами, логистическая регрессия обеспечивает постоянный результат, тогда как линейная регрессия обеспечивает непрерывный результат.

Поскольку результат непрерывен в линейной регрессии, существует бесконечное количество возможных значений результата. Но для логистической регрессии количество возможных значений результата ограничено.

В линейной регрессии зависимые и независимые переменные должны быть линейно связаны. В случае логистической регрессии независимые переменные должны быть линейно связаны с   Лог шансы   (логарифм (p/(1-p)).

В то время как линейная регрессия оценивается с использованием обычного метода наименьших квадратов, логистическая регрессия оценивается с использованием подхода оценки максимального правдоподобия.

И логистическая, и линейная регрессия   контролируемое машинное обучение   алгоритмы и два основных типа регрессионного анализа. В то время как логистическая регрессия используется для решения задач классификации, линейная регрессия в основном используется для задач регрессии.

Возвращаясь к примеру времени, потраченного на учебу, линейная регрессия и логистическая регрессия могут предсказывать разные вещи. Логистическая регрессия может помочь предсказать, сдал ли студент экзамен или нет. Напротив, линейная регрессия может предсказать балл студента.

Предположения логистической регрессии

При использовании логистической регрессии мы делаем несколько предположений. Предположения являются неотъемлемой частью правильного использования логистической регрессии для прогнозирования и решения задач классификации.

Типы логистической регрессии

Логистическую регрессию можно разделить на разные типы в зависимости от количества результатов или категорий зависимой переменной.

Когда мы думаем о логистической регрессии, мы, скорее всего, думаем о бинарной логистической регрессии. В большинстве частей этой статьи, когда мы говорили о логистической регрессии, мы имели в виду бинарную логистическую регрессию.

Ниже приведены три основных типа логистической регрессии.

Бинарная логистическая регрессия

Бинарная логистическая регрессия — это статистический метод, используемый для прогнозирования взаимосвязи между зависимой переменной и независимой переменной. В этом методе зависимая переменная является двоичной переменной, то есть она может принимать только два значения (да или нет, истина или ложь, успех или неудача, 0 или 1).

Простым примером бинарной логистической регрессии является определение того, является ли электронное письмо спамом или нет.

Полиномиальная логистическая регрессия

Полиномиальная логистическая регрессия является расширением бинарной логистической регрессии. Он допускает более двух категорий результата или зависимой переменной.

Это похоже на бинарную логистическую регрессию, но может иметь более двух возможных результатов. Это означает, что переменная результата может иметь три или более возможных неупорядоченных типа — типы, не имеющие количественного значения. Например, зависимая переменная может представлять «Тип A», «Тип B» или «Тип C».

Подобно бинарной логистической регрессии, полиномиальная логистическая регрессия также использует оценку максимального правдоподобия для определения вероятности.

Например, полиномиальную логистическую регрессию можно использовать для изучения взаимосвязи между образованием и выбором профессии. Здесь выбор профессии будет зависимой переменной, состоящей из категорий различных профессий.

Порядковая логистическая регрессия

Порядковая логистическая регрессия , также известная как порядковая регрессия, является еще одним расширением бинарной логистической регрессии. Он используется для прогнозирования зависимой переменной с тремя или более возможными упорядоченными типами — типами, имеющими количественное значение. Например, зависимая переменная может представлять «Совершенно не согласен», «Не согласен», «Согласен» или «Совершенно согласен».

Его можно использовать для определения производительности труда (плохая, средняя или отличная) и удовлетворенности работой (неудовлетворен, удовлетворен или очень удовлетворен).

Преимущества и недостатки логистической регрессии

Многие преимущества и недостатки модели логистической регрессии применимы и к модели линейной регрессии. Одним из наиболее значительных преимуществ модели логистической регрессии является то, что она не просто классифицирует, но и дает вероятности.

Однако у логистической регрессии есть множество недостатков. Если есть функция, которая идеально разделяет два класса, то модель больше не может обучаться. Это называется полным разделением .

Это происходит главным образом потому, что вес для этой функции не будет сходиться, поскольку оптимальный вес будет бесконечным. Однако в большинстве случаев полное разделение может быть решено путем определения априорного распределения вероятностей весов или введения штрафных санкций за веса.

Когда жизнь дает вам варианты, подумайте о логистической регрессии

Многие могут возразить, что люди не живут в бинарном мире, в отличие от компьютеров. Конечно, если вам дадут кусок пиццы и гамбургер, вы можете откусить и то, и другое, не выбирая что-то одно. Но если присмотреться, бинарное решение выгравировано (буквально) на всем. Вы можете либо есть, либо не есть пиццу; нет золотой середины.

Оценка производительности прогностической модели может быть сложной, если объем данных ограничен. Для этого вы можете использовать метод, называемый перекрестной проверкой, который включает в себя разделение доступных данных на обучающий набор и тестовый набор.