Lojistik Regresyon Nedir? Ne Zaman Kullanacağınızı Öğrenin
Yayınlanan: 2021-07-29Hayat zorlu ikili seçeneklerle doludur.
O dilim pizzayı yemeli miyim, yememeli miyim? Şemsiye taşımalı mıyım, taşımamalı mıyım?
Artıları ve eksileri tartarak bazı kararlar doğru bir şekilde verilebilirken - örneğin, fazladan kalori içerdiği için bir dilim pizza yememek daha iyidir - bazı kararlar o kadar kolay olmayabilir.
Örneğin, belirli bir günde yağmur yağıp yağmayacağından asla tam olarak emin olamazsınız. Bu nedenle şemsiye taşıyıp taşımama kararı verilmesi zor bir karardır.
Doğru seçimi yapmak için tahmin yeteneği gerekir. Bu yetenek son derece kazançlıdır ve özellikle bilgisayarlarda çok sayıda gerçek dünya uygulamasına sahiptir. Bilgisayarlar ikili kararları sever. Sonuçta, ikili kodda konuşuyorlar.
Makine öğrenme algoritmalar, daha doğrusu lojistik regresyon algoritması , geçmiş veri noktalarına bakarak olayların olasılığını tahmin etmeye yardımcı olabilir. Örneğin, bir kişinin seçimi kazanıp kazanmayacağını veya bugün yağmur yağıp yağmayacağını tahmin edebilir.
Lojistik regresyon nedir?
Lojistik regresyon, önceki gözlemlere dayalı olarak bağımlı bir değişkenin sonucunu tahmin etmek için kullanılan istatistiksel bir yöntemdir. Bu bir tür regresyon analizidir ve ikili sınıflandırma problemlerini çözmek için yaygın olarak kullanılan bir algoritmadır.
Regresyon analizinin ne olduğunu merak ediyorsanız, bağımlı değişken ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi bulmak için kullanılan bir tür tahmine dayalı modelleme tekniğidir.
Çalışmaya harcanan zaman ve Instagram'da geçirilen zaman bağımsız değişkenlere örnek olarak verilebilir. Bu durumda, notlar bağımlı değişken olacaktır. Çünkü hem "ders çalışmak için harcanan zaman" hem de "Instagram'da geçirilen zaman" notları etkileyecektir; biri olumlu diğeri olumsuz.
Lojistik regresyon, bir dizi bağımsız değişkene dayalı ikili bir sonucu tahmin eden bir sınıflandırma algoritmasıdır . Yukarıdaki örnekte bu, bir sınıfı geçip geçemeyeceğinizi tahmin etmek anlamına gelir. Elbette lojistik regresyon, regresyon problemlerini çözmek için de kullanılabilir, ancak esas olarak sınıflandırma problemlerinde kullanılır.
İpucu: Monoton görevleri otomatikleştirmek ve veriye dayalı kararlar almak için makine öğrenimi yazılımını kullanın.
Başka bir örnek, bir öğrencinin bir üniversiteye kabul edilip edilmeyeceğini tahmin etmek olabilir. Bunun için SAT puanı, öğrencinin not ortalaması ve ders dışı etkinliklerin sayısı gibi birden fazla faktör dikkate alınacaktır. Önceki sonuçlarla ilgili tarihsel verileri kullanan lojistik regresyon algoritması, öğrencileri "kabul" veya "red" kategorilerine ayıracaktır.
Lojistik regresyon ayrıca binom lojistik regresyon veya ikili lojistik regresyon olarak da adlandırılır. Yanıt değişkeninin ikiden fazla sınıfı varsa, buna çok terimli lojistik regresyon denir. Şaşırtıcı olmayan bir şekilde, lojistik regresyon istatistiklerden ödünç alınmıştır ve makine öğrenimi ve veri biliminde en yaygın ikili sınıflandırma algoritmalarından biridir.
Biliyor musun? Bir yapay sinir ağı (YSA) temsili, çok sayıda lojistik regresyon sınıflandırıcısını bir araya toplamak olarak görülebilir.
Lojistik regresyon, bağımlı değişken (tahmin etmek istediğimiz şey) ile bir veya daha fazla bağımsız değişken (özellikler) arasındaki ilişkiyi ölçerek çalışır. Bunu, altta yatan lojistik fonksiyonu yardımıyla olasılıkları tahmin ederek yapar.
Lojistik regresyonda anahtar terimler
Terminolojiyi anlamak, lojistik regresyonun sonuçlarını doğru bir şekilde deşifre etmek için çok önemlidir. İstatistik veya makine öğrenimi konusunda yeniyseniz, belirli terimlerin ne anlama geldiğini bilmek hızlı bir şekilde öğrenmenize yardımcı olacaktır.
- Değişken: Ölçülebilen veya sayılabilen herhangi bir sayı, özellik veya miktar. Yaş, hız, cinsiyet ve gelir örneklerdir.
- Katsayı: Genellikle bir tam sayı olan ve eşlik ettiği değişkenle çarpılan bir sayı. Örneğin, 12y'de 12 sayısı katsayıdır.
- EXP: Üstel ifadenin kısa biçimi.
- Aykırı Değerler: Diğerlerinden önemli ölçüde farklı olan veri noktaları.
- Tahmin edici: Parametrelerin tahminlerini üreten bir algoritma veya formül.
- Ki-kare testi: Ki-kare testi olarak da adlandırılan bu, verilerin beklendiği gibi olup olmadığını kontrol etmek için bir hipotez test yöntemidir.
- Standart hata: İstatistiksel bir örnek popülasyonunun yaklaşık standart sapması.
- Düzenlileştirme: Eğitim veri setine bir fonksiyon (uygun şekilde) yerleştirerek hatayı ve fazla uydurmayı azaltmak için kullanılan bir yöntem.
- Çoklu Bağlantı: İki veya daha fazla bağımsız değişken arasında karşılıklı ilişkilerin bulunması.
- Uyum iyiliği: Bir istatistiksel modelin bir dizi gözleme ne kadar iyi uyduğunun açıklaması.
- Odds oranı: İki olay arasındaki ilişkinin gücünün ölçüsü.
- Log-olasılık fonksiyonları: Bir istatistiksel modelin uyum iyiliğini değerlendirir.
- Hosmer-Lemeshow testi: Gözlenen olay oranlarının beklenen olay oranlarıyla eşleşip eşleşmediğini değerlendiren bir test.
Lojistik fonksiyon nedir?
Lojistik regresyon, adını kalbinde kullanılan fonksiyon olan lojistik fonksiyondan alır. İstatistikçiler başlangıçta bunu nüfus artışının özelliklerini tanımlamak için kullandılar. Sigmoid işlevi ve logit işlevi , lojistik işlevin bazı varyasyonlarıdır. Logit fonksiyonu, standart lojistik fonksiyonun tersidir.
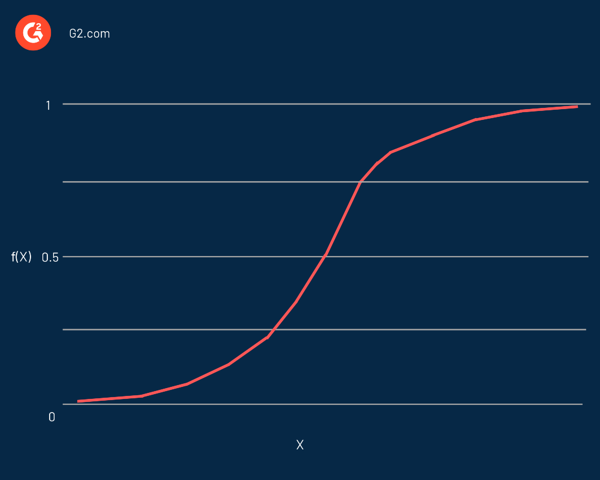
Gerçekte, herhangi bir gerçek sayıyı alıp 0 ile 1 arasında bir değere eşleyebilen, ancak asla tam olarak bu sınırlarda olmayan S şeklinde bir eğridir. Şu denklemle temsil edilir:
f(x) = L / 1 + e^-k(x - x0)
Bu denklemde:
- f(X) fonksiyonun çıktısıdır
- L eğrinin maksimum değeridir
- e doğal logaritmaların tabanıdır
- k eğrinin dikliğidir
- x gerçek sayıdır
- x0 , sigmoid orta noktasının x değerleridir
Öngörülen değer oldukça negatif bir değerse, sıfıra yakın olarak kabul edilir. Öte yandan, tahmin edilen değer anlamlı bir pozitif değer ise, bire yakın kabul edilir.
Lojistik regresyon, düz bir çizgi denklemi kullanılarak lineer regresyonun nasıl tanımlandığına benzer şekilde temsil edilir. Doğrusal regresyondan kayda değer bir fark, çıktının sayısal bir değer yerine ikili bir değer (0 veya 1) olacak olmasıdır.
İşte bir lojistik regresyon denklemi örneği:
y = e^(b0 + b1*x) / (1 + e^(b0 + b1*x))
Bu denklemde:
- y , tahmin edilen değerdir (veya çıktıdır)
- b0 önyargıdır (veya kesme terimidir)
- b1 giriş katsayısıdır
- x tahmin değişkenidir (veya girdidir)
Bağımlı değişken genellikle Bernoulli dağılımı. Katsayıların değerleri, maksimum olabilirlik tahmini (MLE) , gradyan inişi ve stokastik gradyan inişi kullanılarak tahmin edilir.
gibi diğer sınıflandırma algoritmalarında olduğu gibi k-en yakın komşular, bir karışıklık matrisi lojistik regresyon algoritmasının doğruluğunu değerlendirmek için kullanılır.
Biliyor musun? Lojistik regresyon, daha geniş bir genelleştirilmiş doğrusal model ailesinin (GLM'ler) bir parçasıdır.
Bir sınıflandırıcının performansını değerlendirmek gibi, modelin bir gözlemi neden belirli bir şekilde sınıflandırdığını bilmek de aynı derecede önemlidir. Başka bir deyişle, yorumlanabilir olması için sınıflandırıcının kararına ihtiyacımız var.
Yorumlanabilirliği tanımlamak kolay olmasa da, birincil amacı, insanların bir algoritmanın neden belirli bir karar verdiğini bilmesi gerektiğidir. Lojistik regresyon durumunda, aşağıdaki gibi istatistiksel testlerle birleştirilebilir. Wald testi ya da olasılık oranı testi yorumlanabilirlik için.
Lojistik regresyon ne zaman kullanılır?
Kategorik bağımlı değişkeni tahmin etmek için lojistik regresyon uygulanır. Başka bir deyişle, tahmin kategorik olduğunda kullanılır, örneğin evet veya hayır, doğru veya yanlış, 0 veya 1. Lojistik regresyonun tahmini olasılığı veya çıktısı bunlardan biri olabilir ve orta yol yoktur.
Tahmin değişkenleri durumunda, aşağıdaki kategorilerden herhangi birinin parçası olabilirler:
- Sürekli veri: Sonsuz ölçekte ölçülebilen veriler. İki sayı arasında herhangi bir değer alabilir. Örnekler, pound cinsinden ağırlık veya Fahrenheit cinsinden sıcaklıktır.
- Ayrık, nominal veriler: Adlandırılmış kategorilere uyan veriler. Hızlı bir örnek saç rengidir: sarışın, siyah veya kahverengi.
- Ayrık, sıralı veriler: Bir ölçekte bir tür düzene uyan veriler. Bir örnek, bir ila beş arasında bir ölçekte bir ürün veya hizmetten ne kadar memnun olduğunuzu söylemektir.
Lojistik regresyon analizi, bir olayın olasılığını tahmin etmek için değerlidir. Herhangi iki sınıf arasındaki olasılıkları belirlemeye yardımcı olur.

Özetle, tarihsel verilere bakarak lojistik regresyon aşağıdakileri tahmin edebilir:
- Bir e-posta bir spam'dir
- Bugün yağmur yağacak
- Bir tümör ölümcül
- Bir kişi bir araba satın alacak
- Çevrimiçi bir işlem dolandırıcıdır
- Bir yarışmacı seçimi kazanacak
- Bir grup kullanıcı bir ürün satın alacak
- Bir sigorta poliçesi sahibi, poliçe süresi sona ermeden önce sona erer
- Promosyon e-posta alıcısı, yanıt veren veya yanıt vermeyen kişidir
Özünde, lojistik regresyon, olasılık ve sınıflandırma problemlerinin çözülmesine yardımcı olur. Diğer bir deyişle, lojistik regresyondan yalnızca sınıflandırma ve olasılık sonuçları bekleyebilirsiniz.
Örneğin, bir şeyin “doğru ya da yanlış” olma olasılığını belirlemek ve “evet ya da hayır” gibi iki sonuç arasında karar vermek için kullanılabilir.
Bir lojistik regresyon modeli, verileri çıkarma, dönüştürme ve yükleme (ETL) işlemleri için sınıflandırmaya da yardımcı olabilir. Gözlem sayısı öznitelik sayısından az ise lojistik regresyon kullanılmamalıdır. Aksi takdirde aşırı terlemeye neden olabilir.
Doğrusal regresyon ve lojistik regresyon
Lojistik regresyon, bir veya daha fazla bağımsız değişken için kategorik değişkeni tahmin ederken, doğrusal regresyon sürekli değişkeni tahmin eder. Diğer bir deyişle, lojistik regresyon sabit bir çıktı sağlarken, doğrusal regresyon sürekli bir çıktı sunar.
Lineer regresyonda sonuç sürekli olduğundan, sonuç için sonsuz olası değer vardır. Ancak lojistik regresyon için olası sonuç değerlerinin sayısı sınırlıdır.
Doğrusal regresyonda bağımlı ve bağımsız değişkenler doğrusal olarak ilişkili olmalıdır. Lojistik regresyon durumunda, bağımsız değişkenler doğrusal olarak ilişkili olmalıdır. günlük oranları (günlük (p/(1-p))).
İpucu: Lojistik regresyon, R, Python, Java ve MATLAB gibi veri analizi için kullanılan herhangi bir programlama dilinde uygulanabilir.
Doğrusal regresyon, olağan en küçük kareler yöntemi kullanılarak tahmin edilirken, lojistik regresyon, maksimum olabilirlik tahmin yaklaşımı kullanılarak tahmin edilir.
Hem lojistik hem de doğrusal regresyon denetimli makine öğrenimi algoritmalar ve iki ana tip regresyon analizi. Sınıflandırma problemlerini çözmek için lojistik regresyon kullanılırken, regresyon problemleri için öncelikle lineer regresyon kullanılır.
Çalışmaya harcanan zaman örneğine geri dönersek, doğrusal regresyon ve lojistik regresyon farklı şeyleri tahmin edebilir. Lojistik regresyon, öğrencinin bir sınavı geçip geçmediğini tahmin etmeye yardımcı olabilir. Buna karşılık, doğrusal regresyon öğrencinin puanını tahmin edebilir.
Lojistik regresyon varsayımları
Lojistik regresyonu kullanırken birkaç varsayımda bulunuyoruz. Tahminler yapmak ve sınıflandırma problemlerini çözmek için lojistik regresyonu doğru kullanmak için varsayımlar ayrılmaz bir bütündür.
Lojistik regresyonun ana varsayımları şunlardır:
- Bağımsız değişkenler arasında çok az veya hiç çoklu bağlantı yoktur.
- Bağımsız değişkenler , log oranlarıyla (log (p/(1-p)) doğrusal olarak ilişkilidir .
- Bağımlı değişken ikili veya ikili ; iki ayrı kategoriye girer. Bu, yalnızca daha sonra tartışılacak olan ikili lojistik regresyon için geçerlidir.
- Hatalara yol açabilecekleri için anlamsız değişkenler yoktur .
- Veri örneği boyutları daha büyüktür , bu da daha iyi sonuçlar için ayrılmazdır.
- Aykırı değerler yok .
Lojistik regresyon türleri
Lojistik regresyon, bağımlı değişkenin çıktı sayısına veya kategorilerine göre farklı türlere ayrılabilir.
Lojistik regresyonu düşündüğümüzde, büyük olasılıkla ikili lojistik regresyonu düşünüyoruz. Bu makalenin çoğu bölümünde lojistik regresyondan bahsettiğimizde ikili lojistik regresyondan bahsediyorduk.
Aşağıdakiler üç ana lojistik regresyon türüdür.
İkili lojistik regresyon
İkili lojistik regresyon , bağımlı değişken ile bağımsız değişken arasındaki ilişkiyi tahmin etmek için kullanılan istatistiksel bir yöntemdir. Bu yöntemde bağımlı değişken bir ikili değişkendir, yani yalnızca iki değer alabilir (evet veya hayır, doğru veya yanlış, başarı veya başarısızlık, 0 veya 1).
Basit bir ikili lojistik regresyon örneği, bir e-postanın spam olup olmadığını belirlemektir.
Çok terimli lojistik regresyon
Çok terimli lojistik regresyon, ikili lojistik regresyonun bir uzantısıdır. Sonuç veya bağımlı değişkenin ikiden fazla kategorisine izin verir.
İkili lojistik regresyona benzer, ancak ikiden fazla olası sonucu olabilir. Bu, sonuç değişkeninin üç veya daha fazla olası sırasız türe sahip olabileceği anlamına gelir - niceliksel önemi olmayan türler. Örneğin, bağımlı değişken "Tip A", "Tip B" veya "Tip C"yi temsil edebilir.
İkili lojistik regresyona benzer şekilde, çok terimli lojistik regresyon da olasılığı belirlemek için maksimum olabilirlik tahminini kullanır.
Örneğin, çok terimli lojistik regresyon, kişinin eğitimi ile mesleki tercihleri arasındaki ilişkiyi incelemek için kullanılabilir. Burada meslek tercihleri, farklı meslek kategorilerinden oluşan bağımlı değişken olacaktır.
Sıralı lojistik regresyon
Sıralı regresyon olarak da bilinen sıralı lojistik regresyon, ikili lojistik regresyonun başka bir uzantısıdır. Üç veya daha fazla olası sıralı tiple bağımlı değişkeni tahmin etmek için kullanılır - nicel önemi olan tipler. Örneğin, bağımlı değişken "Kesinlikle Katılmıyorum", "Katılıyorum", "Katılıyorum" veya "Kesinlikle Katılıyorum"u temsil edebilir.
İş performansını (zayıf, ortalama veya mükemmel) ve iş memnuniyetini (memnun değil, memnun veya çok memnun) belirlemek için kullanılabilir.
Lojistik regresyonun avantajları ve dezavantajları
Lojistik regresyon modelinin birçok avantajı ve dezavantajı lineer regresyon modeli için geçerlidir. Lojistik regresyon modelinin en önemli avantajlarından biri, sadece sınıflandırma değil, olasılıklar da vermesidir.
Aşağıdakiler, lojistik regresyon algoritmasının avantajlarından bazılarıdır.
- Anlaması basit, uygulaması kolay ve eğitilmesi verimli
- Veri kümesi doğrusal olarak ayrılabilir olduğunda iyi performans gösterir
- Daha küçük veri kümeleri için iyi doğruluk
- Sınıfların dağılımı hakkında herhangi bir varsayımda bulunmaz
- İlişki yönünü sunar (olumlu veya olumsuz)
- Özellikler arasındaki ilişkileri bulmak için kullanışlıdır
- İyi kalibre edilmiş olasılıklar sağlar
- Düşük boyutlu veri kümelerinde fazla uydurmaya daha az eğilimli
- Çok sınıflı sınıflandırmaya genişletilebilir
Bununla birlikte, lojistik regresyonun sayısız dezavantajı vardır. İki sınıfı mükemmel bir şekilde ayıracak bir özellik varsa, model artık eğitilemez. Buna tam ayrılma denir.
Bu, esas olarak, optimal ağırlık sonsuz olacağından, bu özelliğin ağırlığı yakınsamayacağı için olur. Bununla birlikte, çoğu durumda, tam ayırma, ağırlıkların önceden bir olasılık dağılımı tanımlanarak veya ağırlıkların cezalandırılmasıyla çözülebilir.
Lojistik regresyon algoritmasının bazı dezavantajları şunlardır:
- Doğrusal sınırlar oluşturur
- Öznitelik sayısı gözlem sayısından fazlaysa fazla uydurmaya yol açabilir
- Tahmin ediciler ortalamaya sahip olmalı veya çoklu doğrusallık içermemelidir.
- Karmaşık ilişkiler elde etmek için zorlu. Sinir ağları gibi algoritmalar daha uygun ve güçlü
- Yalnızca ayrık işlevleri tahmin etmek için kullanılabilir
- Doğrusal olmayan problemleri çözemez
- Aykırı değerlere duyarlı
Hayat size seçenekler sunduğunda, lojistik gerilemeyi düşünün.
Birçoğu, insanların bilgisayarların aksine ikili bir dünyada yaşamadıklarını iddia edebilir. Tabii ki, bir dilim pizza ve bir hamburger verilirse, birini seçmek zorunda kalmadan ikisinden de bir ısırık alabilirsiniz. Ama daha yakından bakarsanız, (kelimenin tam anlamıyla) her şeye ikili bir karar kazınmıştır. Pizza yemeyi veya yememeyi seçebilirsiniz; ortası yok.
Sınırlı miktarda veri varsa, tahmine dayalı bir modelin performansını değerlendirmek zor olabilir. Bunun için, mevcut verileri bir eğitim seti ve bir test seti olarak bölümlere ayırmayı içeren çapraz doğrulama adı verilen bir teknik kullanabilirsiniz.
