Apa Itu Regresi Logistik? Pelajari Kapan Menggunakannya

Hidup ini penuh dengan pilihan biner yang sulit.

Haruskah saya makan sepotong pizza itu atau tidak? Haruskah saya membawa payung atau tidak?

Sementara beberapa keputusan dapat dibuat dengan tepat dengan mempertimbangkan pro dan kontra – misalnya, lebih baik tidak makan sepotong pizza karena mengandung kalori ekstra – beberapa keputusan mungkin tidak semudah itu.

Misalnya, Anda tidak pernah bisa sepenuhnya yakin apakah akan turun hujan pada hari tertentu atau tidak. Jadi keputusan membawa payung atau tidak adalah keputusan yang sulit.

Untuk membuat pilihan yang tepat, seseorang membutuhkan kemampuan prediktif. Kemampuan ini sangat menguntungkan dan memiliki banyak aplikasi dunia nyata, terutama di komputer. Komputer menyukai keputusan biner. Bagaimanapun, mereka berbicara dalam kode biner.

Pembelajaran mesin   algoritma, lebih tepatnya algoritma regresi logistik , dapat membantu memprediksi kemungkinan peristiwa dengan melihat titik data historis. Misalnya, dapat memprediksi apakah seseorang akan memenangkan pemilihan atau apakah hari ini akan hujan.

Jika Anda bertanya-tanya apa itu analisis regresi , ini adalah jenis teknik pemodelan prediktif yang digunakan untuk menemukan hubungan antara variabel dependen dan satu atau lebih variabel independen.

Contoh variabel bebas adalah waktu yang dihabiskan untuk belajar dan waktu yang dihabiskan di Instagram. Dalam hal ini, nilai akan menjadi variabel terikat. Ini karena "waktu yang dihabiskan untuk belajar" dan "waktu yang dihabiskan di Instagram" akan memengaruhi nilai; satu positif dan yang lainnya negatif.

Regresi logistik adalah algoritma klasifikasi yang memprediksi hasil biner berdasarkan serangkaian variabel independen. Dalam contoh di atas, ini berarti memprediksi apakah Anda akan lulus atau gagal dalam suatu kelas. Tentu saja, regresi logistik juga dapat digunakan untuk menyelesaikan masalah regresi, tetapi terutama digunakan untuk masalah klasifikasi.

Contoh lain adalah memprediksi apakah seorang siswa akan diterima di universitas. Untuk itu, beberapa faktor seperti nilai SAT, nilai rata-rata siswa, dan jumlah kegiatan ekstrakurikuler akan dipertimbangkan. Menggunakan data historis tentang hasil sebelumnya, algoritma regresi logistik akan mengurutkan siswa ke dalam kategori "menerima" atau "menolak".

Regresi logistik juga disebut sebagai regresi logistik binomial atau regresi logistik biner. Jika ada lebih dari dua kelas dari variabel respon disebut regresi logistik multinomial . Tidak mengherankan, regresi logistik dipinjam dari statistik dan merupakan salah satu algoritma klasifikasi biner paling umum dalam pembelajaran mesin dan ilmu data.

Regresi logistik bekerja dengan mengukur hubungan antara variabel dependen (apa yang ingin kita prediksi) dan satu atau lebih variabel independen (fitur). Ini dilakukan dengan memperkirakan probabilitas dengan bantuan fungsi logistik yang mendasarinya.

Istilah kunci dalam regresi logistik

Memahami terminologi sangat penting untuk menguraikan hasil regresi logistik dengan benar. Mengetahui apa arti istilah tertentu akan membantu Anda belajar dengan cepat jika Anda baru mengenal statistik atau pembelajaran mesin.

Apa itu fungsi logistik?

Regresi logistik dinamai sesuai dengan fungsi yang digunakan pada intinya, fungsi logistik . Para ahli statistik awalnya menggunakannya untuk menggambarkan sifat-sifat pertumbuhan penduduk. Fungsi sigmoid dan fungsi logit adalah beberapa variasi dari fungsi logistik. Fungsi logit adalah kebalikan dari fungsi logistik standar.

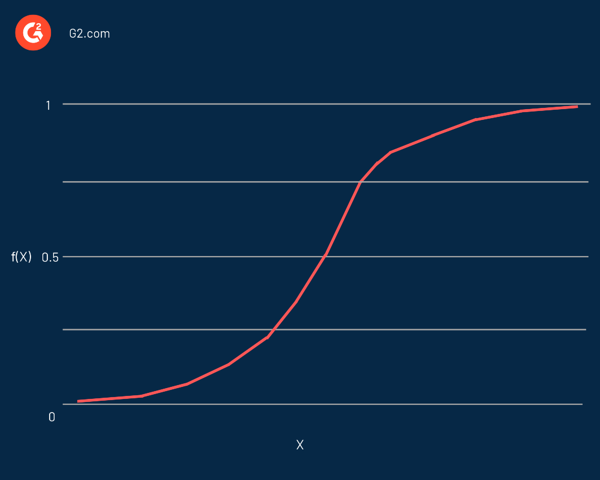
Akibatnya, ini adalah kurva berbentuk S yang mampu mengambil bilangan real apa pun dan memetakannya menjadi nilai antara 0 dan 1, tetapi tidak pernah tepat pada batas tersebut. Itu diwakili oleh persamaan:

Dalam persamaan ini:

• f(X) adalah keluaran dari fungsi
• L adalah nilai maksimum kurva
• e adalah basis dari logaritma natural
• k adalah kecuraman kurva
• x adalah bilangan asli
• x0 adalah nilai x dari titik tengah sigmoid

Jika nilai prediksi adalah nilai negatif yang cukup besar, itu dianggap mendekati nol. Di sisi lain, jika nilai prediksi adalah nilai positif signifikan, itu dianggap mendekati satu.

Regresi logistik direpresentasikan mirip dengan bagaimana regresi linier didefinisikan menggunakan persamaan garis lurus. Perbedaan penting dari regresi linier adalah bahwa output akan menjadi nilai biner (0 atau 1) daripada nilai numerik.

Berikut ini contoh persamaan regresi logistik:

Dalam persamaan ini:

• y adalah nilai prediksi (atau output)
• b0 adalah bias (atau istilah intersep)
• b1 adalah koefisien untuk input
• x adalah variabel prediktor (atau input)

Variabel terikat umumnya mengikuti   distribusi Bernoulli. Nilai koefisien diestimasi menggunakan estimasi kemungkinan maksimum (MLE) , penurunan gradien , dan penurunan gradien stokastik .

Seperti algoritma klasifikasi lainnya seperti   k-tetangga terdekat, a   matriks kebingungan   digunakan untuk mengevaluasi keakuratan algoritma regresi logistik.

Sama seperti mengevaluasi kinerja pengklasifikasi, sama pentingnya untuk mengetahui mengapa model mengklasifikasikan pengamatan dengan cara tertentu. Dengan kata lain, kita membutuhkan keputusan classifier agar dapat diinterpretasikan.

Meskipun interpretabilitas tidak mudah untuk didefinisikan, maksud utamanya adalah bahwa manusia harus tahu mengapa suatu algoritma membuat keputusan tertentu. Dalam kasus regresi logistik, dapat dikombinasikan dengan uji statistik seperti:   Tes Wald   atau   tes rasio kemungkinan   untuk interpretasi.

Kapan menggunakan regresi logistik

Regresi logistik diterapkan untuk memprediksi variabel dependen kategoris. Dengan kata lain, ini digunakan ketika prediksi bersifat kategoris, misalnya ya atau tidak, benar atau salah, 0 atau 1. Probabilitas atau keluaran regresi logistik yang diprediksi dapat salah satunya, dan tidak ada jalan tengah.

Dalam kasus variabel prediktor, mereka dapat menjadi bagian dari salah satu kategori berikut:

• Data berkelanjutan: Data yang dapat diukur dalam skala tak terbatas. Itu dapat mengambil nilai apa pun di antara dua angka. Contohnya adalah berat dalam pound atau suhu dalam Fahrenheit.
• Diskrit, data nominal: Data yang cocok dengan kategori bernama. Contoh singkatnya adalah warna rambut: pirang, hitam, atau cokelat.
• Diskrit, data ordinal: Data yang cocok dengan beberapa bentuk urutan pada skala. Contohnya adalah memberi tahu seberapa puas Anda dengan produk atau layanan dalam skala satu hingga lima.

Analisis regresi logistik berguna untuk memprediksi kemungkinan suatu peristiwa. Ini membantu menentukan probabilitas antara dua kelas.

Intinya, regresi logistik membantu memecahkan masalah probabilitas dan klasifikasi . Dengan kata lain, Anda hanya dapat mengharapkan hasil klasifikasi dan probabilitas dari regresi logistik.

Misalnya, ini dapat digunakan untuk menentukan probabilitas sesuatu menjadi "benar atau salah" dan juga untuk memutuskan antara dua hasil seperti "ya atau tidak".

Model regresi logistik juga dapat membantu mengklasifikasikan data untuk operasi ekstrak, transformasi, dan pemuatan (ETL). Regresi logistik tidak boleh digunakan jika jumlah pengamatan kurang dari jumlah fitur. Jika tidak, dapat menyebabkan overfitting.

Regresi linier vs. regresi logistik

Sementara regresi logistik memprediksi variabel kategori untuk satu atau lebih variabel independen,   regresi linier   memprediksi variabel kontinu. Dengan kata lain, regresi logistik memberikan output yang konstan, sedangkan regresi linier menawarkan output yang berkelanjutan.

Karena hasilnya kontinu dalam regresi linier, ada kemungkinan nilai tak terbatas untuk hasilnya. Tetapi untuk regresi logistik, jumlah nilai hasil yang mungkin terbatas.

Dalam regresi linier, variabel dependen dan independen harus berhubungan secara linier. Dalam kasus regresi logistik, variabel independen harus berhubungan secara linier dengan   peluang masuk   (log (p/(1-p)).

Sementara regresi linier diestimasi menggunakan metode kuadrat terkecil biasa, regresi logistik diestimasi menggunakan pendekatan estimasi kemungkinan maksimum.

Baik regresi logistik maupun regresi linier adalah   pembelajaran mesin yang diawasi   algoritma dan dua jenis utama analisis regresi. Sementara regresi logistik digunakan untuk menyelesaikan masalah klasifikasi, regresi linier terutama digunakan untuk masalah regresi.

Kembali ke contoh waktu yang dihabiskan untuk belajar, regresi linier dan regresi logistik dapat memprediksi hal yang berbeda. Regresi logistik dapat membantu memprediksi apakah siswa lulus ujian atau tidak. Sebaliknya, regresi linier dapat memprediksi nilai siswa.

Asumsi regresi logistik

Saat menggunakan regresi logistik, kami membuat beberapa asumsi. Asumsi merupakan bagian integral untuk menggunakan regresi logistik dengan benar untuk membuat prediksi dan memecahkan masalah klasifikasi.

Jenis regresi logistik

Regresi logistik dapat dibagi menjadi beberapa jenis berdasarkan jumlah hasil atau kategori variabel dependen.

Ketika kita memikirkan regresi logistik, kita kemungkinan besar memikirkan regresi logistik biner. Di sebagian besar artikel ini, ketika kami mengacu pada regresi logistik, kami mengacu pada regresi logistik biner.

Berikut ini adalah tiga jenis utama regresi logistik.

Regresi logistik biner

Regresi logistik biner adalah metode statistik yang digunakan untuk memprediksi hubungan antara variabel dependen dan variabel independen. Dalam metode ini, variabel dependen adalah variabel biner, artinya hanya dapat mengambil dua nilai (ya atau tidak, benar atau salah, berhasil atau gagal, 0 atau 1).

Contoh sederhana dari regresi logistik biner adalah menentukan apakah sebuah email adalah spam atau bukan.

Regresi logistik multinomial

Regresi logistik multinomial merupakan perluasan dari regresi logistik biner. Hal ini memungkinkan lebih dari dua kategori hasil atau variabel dependen.

Ini mirip dengan regresi logistik biner tetapi dapat memiliki lebih dari dua kemungkinan hasil. Ini berarti bahwa variabel hasil dapat memiliki tiga atau lebih jenis yang tidak berurutan – jenis yang tidak memiliki signifikansi kuantitatif. Misalnya, variabel dependen dapat mewakili "Tipe A", "Tipe B", atau "Tipe C".

Mirip dengan regresi logistik biner, regresi logistik multinomial juga menggunakan estimasi kemungkinan maksimum untuk menentukan probabilitas.

Misalnya, regresi logistik multinomial dapat digunakan untuk mempelajari hubungan antara pendidikan seseorang dan pilihan pekerjaan. Di sini, pilihan pekerjaan akan menjadi variabel dependen yang terdiri dari kategori pekerjaan yang berbeda.

Regresi logistik ordinal

Regresi logistik ordinal , juga dikenal sebagai regresi ordinal, adalah perpanjangan lain dari regresi logistik biner. Ini digunakan untuk memprediksi variabel dependen dengan tiga atau lebih kemungkinan tipe terurut – tipe yang memiliki signifikansi kuantitatif. Misalnya, variabel terikat dapat mewakili "Sangat Tidak Setuju", "Tidak Setuju", "Setuju", atau "Sangat Setuju".

Ini dapat digunakan untuk menentukan kinerja pekerjaan (buruk, rata-rata, atau sangat baik) dan kepuasan kerja (tidak puas, puas, atau sangat puas).

Keuntungan dan kerugian dari regresi logistik

Banyak keuntungan dan kerugian dari model regresi logistik yang berlaku untuk model regresi linier. Salah satu keuntungan paling signifikan dari model regresi logistik adalah tidak hanya mengklasifikasikan tetapi juga memberikan probabilitas.

Namun, ada banyak kelemahan regresi logistik. Jika ada fitur yang memisahkan dua kelas dengan sempurna, maka model tersebut tidak dapat dilatih lagi. Ini disebut pemisahan lengkap .

Ini terjadi terutama karena bobot untuk fitur itu tidak akan menyatu karena bobot optimalnya tidak terbatas. Namun, dalam banyak kasus, pemisahan lengkap dapat diselesaikan dengan mendefinisikan distribusi probabilitas bobot sebelumnya atau menerapkan hukuman bobot.

Ketika hidup memberi Anda pilihan, pikirkan regresi logistik

Banyak yang mungkin berpendapat bahwa manusia tidak hidup di dunia biner, tidak seperti komputer. Tentu saja, jika Anda diberi sepotong pizza dan hamburger, Anda bisa menggigit keduanya tanpa harus memilih salah satu saja. Tetapi jika Anda melihatnya lebih dekat, keputusan biner terukir pada (secara harfiah) semuanya. Anda dapat memilih untuk makan atau tidak makan pizza; tidak ada jalan tengah.

Mengevaluasi kinerja model prediktif bisa jadi rumit jika jumlah datanya terbatas. Untuk ini, Anda dapat menggunakan teknik yang disebut validasi silang, yang melibatkan partisi data yang tersedia ke dalam set pelatihan dan set pengujian.