通过推理分析得出正确的结论
已发表: 2020-03-23我们都因时不时下结论而感到内疚。
无论是说服自己没有人会为您努力计划的会议买票,还是提前两小时到达机场根本不够时间,我们都做到了。
在我们的日常生活之外,很容易在工作中得出不准确的结论,无论行业如何。 当我们这样做时,我们本质上是在泛化,但是如果你可以更准确地进行这些泛化呢? 当您运行推理分析测试时,这是可能的。
什么是推理分析?
推论分析用于得出和衡量基于从人口样本中收集的信息得出的关于人口的结论的可靠性。 由于推理分析不会对总体中的每个人进行抽样,因此结果将始终包含某种程度的不确定性。
在深入进行统计分析时,我们要分析的人口规模通常太大,因此无法研究每个人。 在这些情况下,数据是使用特定人群中个体的随机样本收集的。 然后,对数据进行推理分析,得出关于总体人口的结论。
因为通常不可能测量整个人群,推理分析依赖于从人群中的个人样本中收集数据。 从本质上讲,推理分析用于尝试从数据样本中推断出人群可能会想什么或表现出什么。
有两种主要方法可以解决这个问题:
- 估计参数:从数据样本中获取统计数据(如样本均值)并使用它来得出有关总体的某些信息(总体均值)。
- 假设检验:使用数据样本来回答特定的研究问题。
在估计参数时,除了置信区间外,样本还用于估计描述整个总体的值。 然后,创建估计。
在假设检验中,数据用于确定它是否足以支持或拒绝假设。
描述性分析与推理分析
人们最常使用的两种主要统计分析类型是描述性分析和推理分析。 正因为如此,两者相互混淆的情况并不少见,即使它们为数据分析师提供了对所收集数据的不同见解。
虽然无法显示全貌,但当它们一起使用时,它们为数据可视化和预测分析提供了强大的工具,因为它们依赖于同一组数据。
描述性统计分析提供以某种方式描述数据的信息。 这有时是通过使用数据可视化软件制作的图表来完成的,以解释数据呈现的内容。 这种统计分析方法不用于得出结论,仅用于总结信息。
推论统计分析是用于得出结论的方法。 它允许用户根据所分析的样本推断或得出更大群体的趋势。 基本上,它从样本中获取数据,然后对更大的人口或群体做出结论。
这种类型的统计分析通常用于研究样本内变量之间的关系,从而得出准确代表总体的结论和概括。 与描述性分析不同,企业可以检验假设并从这些数据中得出各种结论。

让我们这样想。 你在看一场棒球比赛,询问 100 名球迷是否喜欢热狗。 您可以制作是或否答案的条形图,这将是描述性分析。 或者您可以使用您的研究得出结论,即 93% 的人口(所有棒球场中的所有棒球迷)喜欢热狗,这将是推理分析。
推理分析测试的类型
统计领域有许多类型的推理分析测试。 您选择使用哪一个将取决于您的样本量、您尝试解决的假设以及被测试人口的规模。
线性回归分析
线性回归分析用于理解数据集中两个变量(X 和 Y)之间的关系,作为估计未知变量以对事件和目标进行未来预测的一种方式。
回归分析的主要目标是根据已知(或固定)变量(X 和 Y)的值来估计随机变量 (Z) 的值。 这通常由散点图表示,如下图所示。
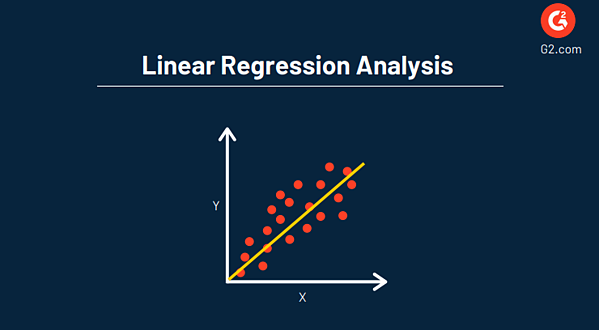
在分析中使用回归的一个关键优势是它提供了对数据的详细查看,并包含一个可用于预测分析和未来优化数据的方程。
回归分析的公式为:
Y = a + b(x)
A→指y截距,x=0时y的值
B→指坡度,或上升超过运行
相关性分析
另一种推理分析测试是相关分析,用于了解两个变量相互依赖的程度。 该分析主要测试两个变量之间关系的强度,以及它们的相关性是强还是弱。
取决于变量,两个变量之间的相关性也可以是负的或正的。 当一个变量的变化不影响另一个变量时,变量被认为是“不相关的”。
这方面的一个例子是价格和需求。 这是因为需求的增加会导致价格的相应上涨。 价格会上涨,因为更多的消费者想要某样东西并且愿意为此付出更多。
总体而言,相关分析的目标是找到显示两个变量之间的关系以及它们如何一起移动的数值。 与回归一样,这通常是通过利用数据可视化软件创建图表来完成的。
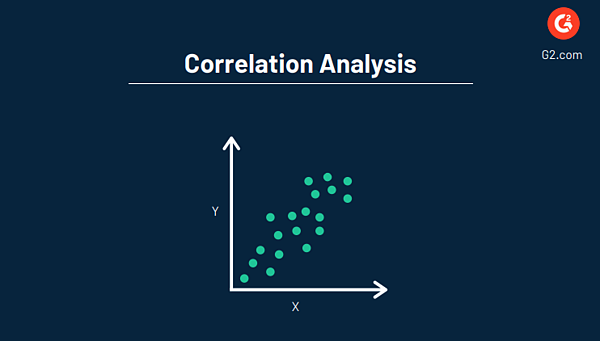
相关:详细了解相关性与回归的来龙去脉,包括差异以及您的企业应使用的方法。
方差分析
方差分析 (ANOVA) 统计方法用于测试和分析数据集中两个或多个均值之间的差异。 这是通过检查样本之间的变化量来完成的。
简而言之,ANOVA 提供了两个或多个总体均值是否相等的统计检验,此外还可以推广两个均值之间的 t 检验。
了解更多: t 检验用于显示两组之间的差异有多显着。 从本质上讲,它允许了解差异(以均值/平均值衡量)是否可能是偶然发生的。

这种方法将允许测试组以查看它们之间是否存在差异。 例如,您可以对参加同一考试的两所不同高中的学生进行测试,以查看一所高中的考试成绩是否高于另一所。
ANOVA也可以分为两种类型:
- 单向:只有一个具有两个水平的自变量。 一个例子是花生酱品牌。
- 双向:两个可以有多个水平的自变量。 一个例子是花生酱品牌和卡路里。
一个级别只是变量内的不同组。 因此,使用与上述相同的示例,花生酱的品牌级别可能是 Jif、Skippy 或 Peter Pan。 卡路里的水平可以是光滑的、奶油的或有机的。
协方差分析
协方差分析 (ANCOVA) 是方差分析 (ANOVA) 和回归分析的独特组合。 ANCOVA 可以显示在一次考虑一个自变量或因素时可以获得哪些额外信息,而不会影响其他变量。
它经常被使用:
- 对于多元回归的扩展,作为比较多元回归线的一种方式
- 控制不是研究重点的协变量(其他变量)
- 对于方差分析的扩展
- 研究其他感兴趣变量的组合
- 控制不能随机但可以测量的因素
当回归均值会影响统计数据的后测测量时,ANCOVA 还可用于对分析进行前测或后测。
例如,假设您的企业为公众生产降低血压的新药物。 您可以进行一项监测四个治疗组和一个对照组的研究。
如果您使用方差分析,您将能够判断治疗是否确实降低了血压。 当您加入 ANCOVA 时,您可以控制可能影响结果的其他因素,例如家庭生活、职业或其他处方药的使用。
置信区间
置信区间是一种用于推断分析的工具,用于估计整个总体的参数,通常是平均值。 从本质上讲,它是任何特定统计数据的不确定性,并且通常在误差范围内使用。
置信区间用一个数字表示,该数字反映了您对调查或民意调查结果是否符合您在可以调查整个人口时所期望的结果的把握程度。
例如,如果民意调查或调查的结果具有 98% 的置信区间,则这定义了您可以 98% 确定包含总体均值的值范围。 要得出这个结论,需要三个信息:
- 置信水平:描述与采样方法相关的不确定性
- 统计数据:从调查或民意调查中收集的数据
- 误差范围:您的结果将与实际人口值相差多少个百分点
卡方检验
卡方检验,也称为 x2 检验,用于在所有变量都是名义变量(也称为值没有数值的变量)时识别组之间的差异,例如性别、工资差距、政治派别等等。
这些测试通常与特定的列联表一起使用,这些列联表根据共同特征对观察进行分组。
卡方检验可以回答的问题可能是:
- 美国所有人的教育水平和婚姻状况是否相关?
- 选民意图和政党成员之间有关系吗?
- 性别会影响人们喜欢哪个假期吗?
通常,这些测试是使用称为简单随机抽样的统计分析方法完成的,以从特定样本中收集数据,从而可能得出准确的结论。 如果我们使用上面列出的第一个问题,数据可能如下所示:
| 姓名 | 地位 | 教育 | |
| 1 | 梅丽莎 | 离婚 | 博士或以上 |
| 2 | 凯西 | 已婚 | 学士学位 |
| 3 | 安吉拉 | 已婚 | 盖德 |
| 4 | 艾丽莎 | 寡 | 学士学位 |
| 5 | 珍娜 | 从未结婚 | 盖德 |
这些列联表用作组织通过简单随机抽样收集的数据的起点。
推理分析的优点
使用推理分析有很多优点,主要是它提供了丰富的详细信息——比运行描述性分析测试后的信息要多得多。
这些信息为研究人员和分析师提供了对两个变量之间关系的全面洞察。 它还可以显示对因果关系的认识以及对整个行业趋势和模式的预测。
此外,由于它在商界和学术界如此广泛使用,因此它是一种普遍接受的统计分析方法。
推理分析的局限性
在推论统计方面,有两个主要限制。
第一个限制来自这样一个事实,即由于正在分析的数据来自尚未完全测量的人群,因此数据分析师无法 100% 确定正在计算的统计数据是正确的。 由于推理分析是基于使用样本中测量的值来得出将从总人口中测量的值的过程,因此结果总是存在一定程度的不确定性。
第二个限制是一些推理测试需要分析师或研究人员根据理论做出有根据的猜测来运行测试。 与第一个限制类似,这些猜测也存在不确定性,这也意味着对某些统计检验结果的可靠性产生一些影响。
不要妄下结论
在您跳到关于数据的可能不准确的结论之前,请确保利用推理分析测试中等待的信息。
无论您希望得出哪种类型的结论,或者您开始的假设是什么,您都可能会对推理分析测试可以带来的结果感到惊讶。
寻找统计分析软件来更好地解释您的所有数据集? 或者也许是一个工具,即使是最复杂的统计分析也能变得简单而有说服力? 查看我们对 G2 的公正评论列表!
