Arrivez à la bonne conclusion avec l'analyse inférentielle
Publié: 2020-03-23Nous sommes tous coupables de sauter aux conclusions de temps en temps.
Qu'il s'agisse de vous convaincre que personne n'achètera de billet pour la conférence que vous avez travaillé si dur à planifier ou qu'arriver à l'aéroport deux heures à l'avance n'est tout simplement pas suffisant, nous l'avons tous fait.
En dehors de notre vie quotidienne, il est facile de tirer des conclusions inexactes au travail, quel que soit le secteur. Lorsque nous faisons cela, nous généralisons essentiellement, mais que se passerait-il si vous pouviez faire ces généralisations avec plus de précision ? C'est possible lorsque vous exécutez des tests d'analyse inférentielle.
Qu'est-ce que l'analyse inférentielle ?
L'analyse inférentielle est utilisée pour tirer et mesurer la fiabilité des conclusions sur une population qui sont basées sur des informations recueillies auprès d'un échantillon de la population. Étant donné que l'analyse inférentielle n'échantillonne pas tout le monde dans une population, les résultats contiendront toujours un certain niveau d'incertitude.
Lorsque nous plongeons dans l'analyse statistique, la taille de la population que nous cherchons à analyser est souvent trop importante, ce qui rend impossible l'étude de tout le monde. Dans ces cas, les données sont collectées à l'aide d'échantillons aléatoires d'individus au sein d'une population spécifique. Ensuite, une analyse inférentielle est utilisée sur les données pour tirer des conclusions sur la population globale.
Parce qu'il est souvent impossible de mesurer une population entière de personnes, l'analyse inférentielle repose sur la collecte de données auprès d'un échantillon d'individus au sein de la population. Essentiellement, l'analyse inférentielle est utilisée pour essayer de déduire à partir d'un échantillon de données ce que la population pourrait penser ou montrer.
Il existe deux manières principales de procéder :
- Estimation des paramètres : prendre une statistique à partir d'un échantillon de données (comme la moyenne de l'échantillon) et l'utiliser pour conclure quelque chose sur la population (la moyenne de la population).
- Tests d'hypothèse : L'utilisation d'échantillons de données pour répondre à des questions de recherche spécifiques.
Dans l'estimation des paramètres, l'échantillon est utilisé pour estimer une valeur qui décrit l'ensemble de la population, en plus d'un intervalle de confiance. Ensuite, le devis est créé.
Dans les tests d'hypothèses, les données sont utilisées pour déterminer si elles sont suffisamment solides pour soutenir ou rejeter une hypothèse.
Analyse descriptive vs analyse inférentielle
Les deux principaux types d'analyse statistique que les gens utilisent le plus souvent sont l'analyse descriptive et l'analyse inférentielle. Pour cette raison, il n'est pas rare que les deux soient confondus, même s'ils fournissent aux analystes de données des informations différentes sur les données collectées.
Bien qu'on ne puisse pas montrer l'image entière, lorsqu'ils sont utilisés ensemble, ils fournissent un outil puissant pour la visualisation des données et l'analyse des prévisions, car ils reposent sur le même ensemble de données.
L'analyse statistique descriptive donne des informations qui décrivent les données d'une certaine manière. Cela se fait parfois avec des tableaux et des graphiques réalisés avec un logiciel de visualisation de données pour expliquer ce que les données présentent. Cette méthode d'analyse statistique n'est pas utilisée pour tirer des conclusions, mais uniquement pour résumer les informations.
L'analyse statistique inférentielle est la méthode qui sera utilisée pour tirer les conclusions. Il permet aux utilisateurs de déduire ou de conclure des tendances sur une population plus large en fonction des échantillons analysés. Fondamentalement, il prend des données à partir d'un échantillon et tire ensuite des conclusions sur une population ou un groupe plus large.
Ce type d'analyse statistique est souvent utilisé pour étudier la relation entre les variables au sein d'un échantillon, permettant des conclusions et des généralisations qui représentent avec précision la population. Et contrairement à l'analyse descriptive, les entreprises peuvent tester une hypothèse et tirer diverses conclusions à partir de ces données.

Pensons-y de cette façon. Vous assistez à un match de baseball et demandez à un échantillon de 100 fans s'ils aiment les hot-dogs. Vous pourriez faire un graphique à barres de réponses oui ou non, ce qui serait une analyse descriptive. Ou vous pourriez utiliser vos recherches pour conclure que 93% de la population (tous les fans de baseball dans tous les stades de baseball) aiment les hot-dogs, ce qui serait une analyse inférentielle.
Types de tests d'analyse inférentielle
Il existe de nombreux types de tests d'analyse inférentielle dans le domaine des statistiques. Celui que vous choisirez d'utiliser dépendra de la taille de votre échantillon, de l'hypothèse que vous essayez de résoudre et de la taille de la population testée.
Analyse de régression linéaire
L'analyse de régression linéaire est utilisée pour comprendre la relation entre deux variables (X et Y) dans un ensemble de données afin d'estimer la variable inconnue pour faire des projections futures sur les événements et les objectifs.
L'objectif principal de l'analyse de régression est d'estimer les valeurs d'une variable aléatoire (Z) en fonction des valeurs de vos variables connues (ou fixes) (X et Y). Ceci est généralement représenté par un nuage de points, comme celui ci-dessous.
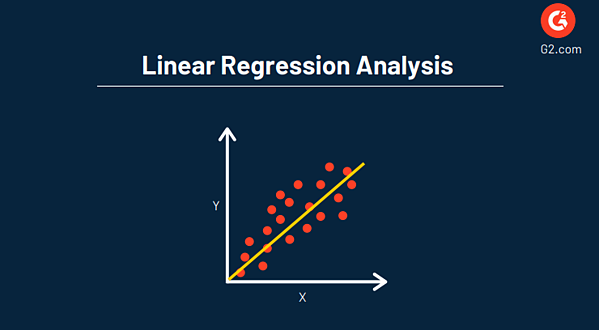
L'un des principaux avantages de l'utilisation de la régression dans votre analyse est qu'elle fournit un aperçu détaillé des données et inclut une équation qui peut être utilisée pour l'analyse prédictive et l'optimisation des données à l'avenir.
La formule de l'analyse de régression est la suivante :
Y = a + b(x)
A → fait référence à l'ordonnée à l'origine, la valeur de y lorsque x = 0
B → fait référence à la pente ou à la montée par rapport à la course
Analyse de corrélation
Un autre test d'analyse inférentielle est l'analyse de corrélation, qui est utilisée pour comprendre dans quelle mesure deux variables dépendent l'une de l'autre. Cette analyse teste essentiellement la force de la relation entre deux variables, et si leur corrélation est forte ou faible.
La corrélation entre deux variables peut également être négative ou positive, selon les variables. Les variables sont considérées comme « non corrélées » lorsqu'un changement dans l'une n'affecte pas l'autre.
Un exemple de ceci serait le prix et la demande. En effet, une augmentation de la demande entraîne une augmentation correspondante des prix. Le prix augmenterait parce que plus de consommateurs veulent quelque chose et sont prêts à payer plus pour cela.
Dans l'ensemble, l'objectif de l'analyse de corrélation est de trouver la valeur numérique qui montre la relation entre les deux variables et comment elles évoluent ensemble. Comme la régression, cela se fait généralement en utilisant un logiciel de visualisation de données pour créer un graphique.
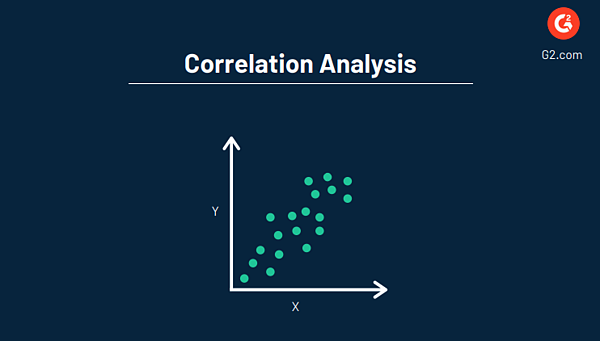
Connexe : En savoir plus sur les tenants et les aboutissants des corrélations par rapport à la régression, y compris les différences et la méthode que votre entreprise devrait utiliser.
Analyse de variance
La méthode statistique d'analyse de la variance (ANOVA) est utilisée pour tester et analyser les différences entre deux ou plusieurs moyennes d'un ensemble de données. Ceci est fait en examinant la quantité de variation entre les échantillons.
En termes simples, l'ANOVA fournit un test statistique pour déterminer si deux ou plusieurs moyennes de population sont égales, en plus de généraliser le test t entre deux moyennes.

En savoir plus : Un test t est utilisé pour montrer l'importance des différences entre deux groupes. Essentiellement, cela permet de comprendre si des différences (mesurées en moyennes/moyennes) ont pu se produire par hasard.
Cette méthode permettra de tester des groupes pour voir s'il y a une différence entre eux. Par exemple, vous pouvez tester les élèves de deux lycées différents qui passent le même examen pour voir si un lycée obtient des résultats supérieurs à l'autre.
L'ANOVA peut également être décomposée en deux types :
- Unidirectionnel : Une seule variable indépendante à deux niveaux. Un exemple serait une marque de beurre de cacahuète.
- Bidirectionnel : Deux variables indépendantes pouvant avoir plusieurs niveaux. Un exemple serait une marque de beurre d'arachide et les calories.
Un niveau est simplement les différents groupes au sein de la variable. Ainsi, en utilisant le même exemple que ci-dessus, les niveaux des marques de beurre de cacahuète pourraient être Jif, Skippy ou Peter Pan. Les niveaux de calories peuvent être lisses, crémeux ou organiques.
Analyse de covariance
L'analyse de covariance (ANCOVA) est un mélange unique d'analyse de variance (ANOVA) et de régression. L'ANCOVA peut montrer quelles informations supplémentaires sont disponibles lors de l'examen d'une variable ou d'un facteur indépendant à la fois, sans influencer les autres.
Il est souvent utilisé :
- Pour une extension de la régression multiple comme moyen de comparer plusieurs droites de régression
- Pour contrôler les covariables (autres variables) qui ne sont pas l'objet principal de votre étude
- Pour une extension de l'analyse de variance
- Pour étudier des combinaisons d'autres variables d'intérêt
- Pour contrôler les facteurs qui ne peuvent pas être randomisés mais qui peuvent être mesurés
L'ANCOVA peut également être utilisée pour pré-tester ou post-tester une analyse lorsque la régression à la moyenne affectera votre mesure post-test de la statistique.
Par exemple, supposons que votre entreprise crée de nouveaux produits pharmaceutiques pour le public qui abaissent la tension artérielle. Vous pouvez mener une étude qui surveille quatre groupes de traitement et un groupe témoin.
Si vous utilisez l'ANOVA, vous serez en mesure de dire si le traitement fait effectivement baisser la tension artérielle. Lorsque vous incorporez l'ANCOVA, vous pouvez contrôler d'autres facteurs susceptibles d'influencer le résultat, comme la vie de famille, la profession ou la consommation d'autres médicaments sur ordonnance.
Intervalle de confiance
Un intervalle de confiance est un outil utilisé dans l'analyse inférentielle qui estime un paramètre, généralement la moyenne, d'une population entière. Essentiellement, il s'agit du degré d'incertitude avec une statistique particulière et est généralement utilisé avec une marge d'erreur.
L'intervalle de confiance est exprimé par un nombre qui reflète votre degré de certitude que les résultats de l'enquête ou du sondage correspondent à ce à quoi vous vous attendriez s'il était possible d'enquêter sur l'ensemble de la population.
Par exemple, si les résultats d'un sondage ou d'une enquête ont un intervalle de confiance de 98 %, cela définit la plage de valeurs dont vous pouvez être sûr à 98 % qu'elle contient la moyenne de la population. Pour arriver à cette conclusion, trois informations sont nécessaires :
- Niveau de confiance : Décrit l'incertitude associée à une méthode d'échantillonnage
- Statistique : données recueillies à partir de l'enquête ou du sondage
- Marge d'erreur : combien de points de pourcentage vos résultats différeront de la valeur réelle de la population
Test du chi carré
Un test du chi carré, également connu sous le nom de test x2, est utilisé pour identifier la différence entre les groupes lorsque toutes les variables sont nominales (également appelées, une variable avec des valeurs qui n'ont pas de valeur numérique), comme le sexe, écart salarial, affiliation politique, etc.
Ces tests sont généralement utilisés avec des tableaux de contingence spécifiques qui regroupent les observations en fonction de caractéristiques communes.
Les questions auxquelles le test du chi carré pourrait répondre pourraient être :
- Le niveau d'éducation et l'état matrimonial sont-ils liés pour toutes les personnes aux États-Unis ?
- Existe-t-il une relation entre l'intention des électeurs et l'appartenance à un parti politique ?
- Le sexe affecte-t-il les vacances que les gens préfèrent ?
Habituellement, ces tests sont effectués en utilisant la méthode d'analyse statistique appelée échantillonnage aléatoire simple pour collecter des données à partir d'un échantillon spécifique pour potentiellement arriver à une conclusion précise. Si nous utilisons la première question ci-dessus, les données peuvent ressembler à :
| Nom | Statut | Éducation | |
| 1 | Mélisse | Divorcé | Doctorat ou supérieur |
| 2 | Casey | Marié | licence |
| 3 | Angèle | Marié | DEG |
| 4 | Alyssa | Veuve | licence |
| 5 | Jenna | Jamais marié | DEG |
Ces tableaux de contingence sont utilisés comme point de départ pour organiser les données recueillies par échantillonnage aléatoire simple.
Avantages de l'analyse inférentielle
L'utilisation de l'analyse inférentielle présente de nombreux avantages, principalement le fait qu'elle fournit un surplus d'informations détaillées - bien plus que ce que vous auriez après avoir exécuté un test d'analyse descriptive.
Ces informations fournissent aux chercheurs et aux analystes un aperçu complet des relations entre deux variables. Il peut également montrer une prise de conscience des causes et des effets et des prédictions concernant les tendances et les modèles dans les industries.
De plus, comme il est si largement utilisé dans le monde des affaires ainsi que dans le milieu universitaire, il s'agit d'une méthode d'analyse statistique universellement acceptée.
Limites de l'analyse inférentielle
En ce qui concerne les statistiques inférentielles, il existe deux principales limites.
La première limite vient du fait que, puisque les données analysées proviennent d'une population qui n'a pas été entièrement mesurée, les analystes de données ne peuvent jamais être sûrs à 100 % que les statistiques calculées sont correctes. Étant donné que l'analyse inférentielle est basée sur le processus d'utilisation des valeurs mesurées dans un échantillon pour conclure les valeurs qui seraient mesurées à partir de la population totale, il y aura toujours un certain niveau d'incertitude concernant les résultats.
La deuxième limitation est que certains tests inférentiels exigent que l'analyste ou le chercheur fasse une supposition éclairée basée sur des théories pour exécuter les tests. Semblable à la première limitation, il y aura une incertitude entourant ces suppositions, ce qui signifiera également des répercussions sur la fiabilité des résultats de certains tests statistiques.
Ne sautez pas aux conclusions
Avant de sauter à une conclusion potentiellement inexacte concernant les données, assurez-vous de tirer parti des informations qui vous attendent dans un test d'analyse inférentielle.
Peu importe le type de conclusion que vous cherchez à tirer ou l'hypothèse avec laquelle vous partez, vous pourriez être surpris par les résultats qu'un test d'analyse inférentielle peut apporter.
Vous recherchez un logiciel d'analyse statistique pour mieux interpréter tous vos ensembles de données ? Ou peut-être un outil qui rend simple et concluante même l'analyse statistique la plus complexe ? Consultez notre liste d'avis impartiaux sur G2 !
