Sampai pada Kesimpulan yang Tepat dengan Analisis Inferensial
Diterbitkan: 2020-03-23Kita semua bersalah karena melompat ke kesimpulan dari waktu ke waktu.
Entah itu meyakinkan diri sendiri bahwa tidak ada yang akan membeli tiket untuk konferensi yang telah Anda rencanakan dengan susah payah atau bahwa tiba di bandara dua jam sebelumnya tidak cukup waktu, kita semua telah melakukannya.
Di luar kehidupan kita sehari-hari, mudah untuk mengambil kesimpulan yang tidak akurat di tempat kerja, apa pun industrinya. Ketika kami melakukan ini, kami pada dasarnya menggeneralisasi, tetapi bagaimana jika Anda dapat membuat generalisasi ini lebih akurat? Itu mungkin ketika Anda menjalankan tes analisis inferensial.
Apa itu analisis inferensial?
Analisis inferensial digunakan untuk menarik dan mengukur keandalan kesimpulan tentang suatu populasi yang didasarkan pada informasi yang dikumpulkan dari sampel populasi. Karena analisis inferensial tidak mengambil sampel semua orang dalam suatu populasi, hasilnya akan selalu mengandung beberapa tingkat ketidakpastian.
Saat menyelami analisis statistik, seringkali ukuran populasi yang ingin kita analisis terlalu besar, sehingga mustahil untuk mempelajari semua orang. Dalam kasus ini, data dikumpulkan dengan menggunakan sampel acak individu dalam populasi tertentu. Kemudian, analisis inferensial digunakan pada data untuk sampai pada kesimpulan tentang populasi secara keseluruhan.
Karena seringkali tidak mungkin untuk mengukur seluruh populasi orang, analisis inferensial bergantung pada pengumpulan data dari sampel individu dalam populasi. Pada dasarnya, analisis inferensial digunakan untuk mencoba menyimpulkan dari sampel data apa yang mungkin dipikirkan atau ditunjukkan oleh populasi.
Ada dua cara utama untuk melakukan ini:
- Memperkirakan parameter: Mengambil statistik dari sampel data (seperti rata-rata sampel) dan menggunakannya untuk menyimpulkan sesuatu tentang populasi (rata-rata populasi).
- Uji hipotesis: Penggunaan sampel data untuk menjawab pertanyaan penelitian tertentu.
Dalam menaksir parameter, sampel digunakan untuk mengestimasi suatu nilai yang menggambarkan seluruh populasi, selain selang kepercayaan. Kemudian, perkiraan dibuat.
Dalam pengujian hipotesis, data digunakan untuk menentukan apakah data tersebut cukup kuat untuk mendukung atau menolak suatu asumsi.
Analisis deskriptif vs. analisis inferensial
Dua jenis utama analisis statistik yang paling sering digunakan orang adalah analisis deskriptif dan analisis inferensial. Karena itu, tidak jarang keduanya menjadi bingung satu sama lain, meskipun mereka memberi analis data wawasan yang berbeda tentang data yang dikumpulkan.
Meskipun seseorang tidak dapat menampilkan keseluruhan gambar, ketika digunakan bersama, mereka menyediakan alat yang kuat ke dalam visualisasi data dan analitik prediksi, karena mereka mengandalkan kumpulan data yang sama.
Analisis statistik deskriptif memberikan informasi yang menggambarkan data dalam beberapa cara. Hal ini terkadang dilakukan dengan bagan dan grafik yang dibuat dengan perangkat lunak visualisasi data untuk menjelaskan apa yang disajikan oleh data tersebut. Metode analisis statistik ini tidak digunakan untuk menarik kesimpulan, hanya untuk meringkas informasi.
Analisis statistik inferensial adalah metode yang akan digunakan untuk menarik kesimpulan. Ini memungkinkan pengguna untuk menyimpulkan atau menyimpulkan tren tentang populasi yang lebih besar berdasarkan sampel yang dianalisis. Pada dasarnya, dibutuhkan data dari sampel dan kemudian membuat kesimpulan tentang populasi atau kelompok yang lebih besar.
Jenis analisis statistik ini sering digunakan untuk mempelajari hubungan antara variabel dalam sampel, memungkinkan kesimpulan dan generalisasi yang secara akurat mewakili populasi. Dan tidak seperti analisis deskriptif, bisnis dapat menguji hipotesis dan menghasilkan berbagai kesimpulan dari data ini.

Mari kita berpikir seperti ini. Anda berada di pertandingan bisbol dan menanyakan sampel 100 penggemar apakah mereka menyukai hotdog. Anda bisa membuat grafik batang jawaban ya atau tidak, yang akan menjadi analisis deskriptif. Atau Anda dapat menggunakan penelitian Anda untuk menyimpulkan bahwa 93% populasi (semua penggemar bisbol di semua stadion bisbol) menyukai hotdog, yang akan menjadi analisis inferensial.
Jenis tes analisis inferensial
Ada banyak jenis tes analisis inferensial yang ada di bidang statistik. Yang mana yang Anda pilih untuk digunakan akan bergantung pada ukuran sampel Anda, hipotesis yang Anda coba pecahkan, dan ukuran populasi yang sedang diuji.
Analisis regresi linier
Analisis regresi linier digunakan untuk memahami hubungan antara dua variabel (X dan Y) dalam kumpulan data sebagai cara untuk memperkirakan variabel yang tidak diketahui untuk membuat proyeksi masa depan pada peristiwa dan tujuan.
Tujuan utama dari analisis regresi adalah untuk memperkirakan nilai variabel acak (Z) berdasarkan nilai variabel yang diketahui (atau tetap) (X dan Y). Ini biasanya diwakili oleh plot pencar, seperti di bawah ini.
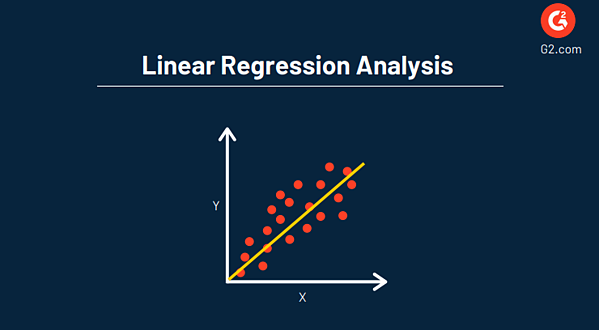
Salah satu keuntungan utama menggunakan regresi dalam analisis Anda adalah ia memberikan tampilan data yang mendetail dan menyertakan persamaan yang dapat digunakan untuk analisis prediktif dan mengoptimalkan data di masa mendatang.
Rumus untuk analisis regresi adalah:
Y = a + b(x)
A → mengacu pada perpotongan y, nilai y ketika x = 0
B → mengacu pada kemiringan, atau naik di atas run
Analisis korelasi
Uji analisis inferensial lainnya adalah analisis korelasi, yang digunakan untuk memahami sejauh mana dua variabel bergantung satu sama lain. Analisis ini pada dasarnya menguji kekuatan hubungan antara dua variabel, dan apakah korelasinya kuat atau lemah.
Korelasi antara dua variabel juga bisa negatif atau positif, tergantung pada variabelnya. Variabel dianggap "tidak berkorelasi" ketika perubahan dalam satu tidak mempengaruhi yang lain.
Contohnya adalah harga dan permintaan. Hal ini karena peningkatan permintaan menyebabkan kenaikan harga yang sesuai. Harga akan meningkat karena lebih banyak konsumen menginginkan sesuatu dan bersedia membayar lebih untuk itu.
Secara keseluruhan, tujuan dari analisis korelasi adalah untuk menemukan nilai numerik yang menunjukkan hubungan antara dua variabel dan bagaimana mereka bergerak bersama. Seperti regresi, ini biasanya dilakukan dengan memanfaatkan perangkat lunak visualisasi data untuk membuat grafik.
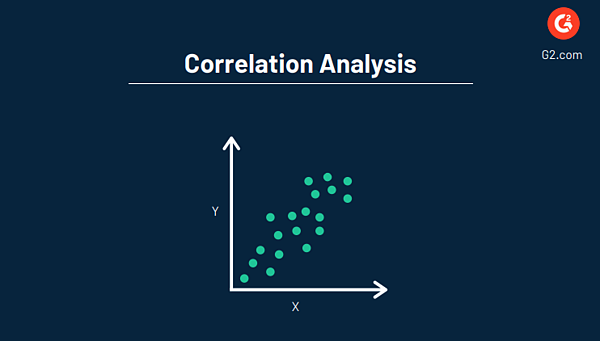
Terkait: Pelajari lebih lanjut tentang seluk beluk korelasi vs regresi, termasuk perbedaan dan metode mana yang harus digunakan bisnis Anda.
Analisis varians
Analisis varians (ANOVA) metode statistik digunakan untuk menguji dan menganalisis perbedaan antara dua atau lebih rata -rata dari kumpulan data. Hal ini dilakukan dengan memeriksa jumlah variasi antara sampel.
Dalam istilah yang paling sederhana, ANOVA menyediakan uji statistik apakah dua atau lebih rata-rata populasi adalah sama, selain menggeneralisasi uji-t antara dua rata-rata.

Pelajari lebih lanjut: Uji-t digunakan untuk menunjukkan seberapa signifikan perbedaan antara dua kelompok. Pada dasarnya, ini memungkinkan pemahaman jika perbedaan (diukur dalam cara/rata-rata) bisa terjadi secara kebetulan.
Metode ini akan memungkinkan pengujian kelompok untuk melihat apakah ada perbedaan di antara mereka. Misalnya, Anda dapat menguji siswa di dua sekolah menengah berbeda yang mengikuti ujian yang sama untuk melihat apakah satu sekolah menengah memiliki nilai lebih tinggi dari yang lain.
ANOVA juga dapat dipecah menjadi dua jenis:
- Satu arah: Hanya satu variabel bebas dengan dua tingkat. Contohnya adalah merek selai kacang.
- Dua arah: Dua variabel independen yang dapat memiliki beberapa level. Contohnya adalah merek selai kacang dan kalorinya.
Tingkat hanyalah kelompok yang berbeda dalam variabel. Jadi, menggunakan contoh yang sama seperti di atas, level merek selai kacang mungkin Jif, Skippy, atau Peter Pan. Tingkat kalori bisa halus, lembut, atau organik.
Analisis kovarians
Analisis kovarians (ANCOVA) adalah perpaduan unik dari analisis varians (ANOVA) dan regresi. ANCOVA dapat menunjukkan informasi tambahan apa yang tersedia ketika mempertimbangkan satu variabel independen, atau faktor, pada satu waktu, tanpa mempengaruhi yang lain.
Ini sering digunakan:
- Untuk perpanjangan regresi berganda sebagai cara untuk membandingkan beberapa garis regresi
- Untuk mengontrol kovariat (variabel lain) yang bukan fokus utama studi Anda
- Untuk perluasan analisis varians
- Untuk mempelajari kombinasi variabel lain yang menarik
- Untuk mengontrol faktor-faktor yang tidak dapat diacak tetapi dapat diukur
ANCOVA juga dapat digunakan untuk melakukan pretest atau posttest suatu analisis ketika regresi terhadap mean akan mempengaruhi pengukuran statistik posttest Anda.
Sebagai contoh, katakanlah bisnis Anda menciptakan obat-obatan baru untuk masyarakat yang menurunkan tekanan darah. Anda dapat melakukan penelitian yang memantau empat kelompok perlakuan dan satu kelompok kontrol.
Jika Anda menggunakan ANOVA, Anda akan dapat mengetahui apakah pengobatan tersebut benar-benar menurunkan tekanan darah. Ketika Anda memasukkan ANCOVA, Anda dapat mengontrol faktor-faktor lain yang mungkin mempengaruhi hasil, seperti kehidupan keluarga, pekerjaan, atau penggunaan obat resep lainnya.
Interval kepercayaan
Interval kepercayaan adalah alat yang digunakan dalam analisis inferensial yang memperkirakan parameter, biasanya rata-rata, dari seluruh populasi. Pada dasarnya, ini adalah seberapa banyak ketidakpastian yang ada dengan statistik tertentu dan biasanya digunakan dengan margin kesalahan.
Interval kepercayaan dinyatakan dengan angka yang mencerminkan seberapa yakin Anda bahwa hasil survei atau jajak pendapat adalah apa yang Anda harapkan jika mungkin untuk mensurvei seluruh populasi.
Misalnya, jika hasil jajak pendapat atau survei memiliki interval kepercayaan 98%, maka ini menentukan rentang nilai yang Anda yakini 98% berisi rata-rata populasi. Untuk sampai pada kesimpulan ini, diperlukan tiga informasi:
- Tingkat kepercayaan : Menjelaskan ketidakpastian yang terkait dengan metode pengambilan sampel
- Statistik: Data yang dikumpulkan dari survei atau jajak pendapat
- Margin of error : Berapa poin persentase hasil Anda akan berbeda dari nilai populasi sebenarnya
Tes chi-kuadrat
Tes chi-kuadrat, atau dikenal sebagai tes x2, digunakan untuk mengidentifikasi perbedaan antara kelompok ketika semua variabel adalah nominal (juga dikenal sebagai, variabel dengan nilai yang tidak memiliki nilai numerik), seperti jenis kelamin, kesenjangan gaji, afiliasi politik, dan sebagainya.
Tes ini biasanya digunakan dengan tabel kontingensi khusus yang mengelompokkan pengamatan berdasarkan karakteristik umum.
Pertanyaan yang dapat dijawab oleh uji chi-kuadrat adalah:
- Apakah tingkat pendidikan dan status perkawinan terkait untuk semua orang di Amerika Serikat?
- Apakah ada hubungan antara niat pemilih dan keanggotaan partai politik?
- Apakah jenis kelamin memengaruhi liburan yang disukai orang?
Biasanya, tes ini dilakukan dengan menggunakan metode analisis statistik yang disebut simple random sampling untuk mengumpulkan data dari sampel tertentu untuk berpotensi sampai pada kesimpulan yang akurat. Jika kita menggunakan pertanyaan pertama yang tercantum di atas, datanya mungkin terlihat seperti:
| Nama | Status | Pendidikan | |
| 1 | Melissa | Cerai | PhD atau lebih tinggi |
| 2 | Casey | Telah menikah | Sarjana |
| 3 | Angela | Telah menikah | GED |
| 4 | Alyssa | Janda | Sarjana |
| 5 | Jenna | Tidak pernah menikah | GED |
Tabel kontingensi ini digunakan sebagai titik awal untuk mengatur data yang dikumpulkan melalui simple random sampling.
Keuntungan dari analisis inferensial
Ada banyak keuntungan menggunakan analisis inferensial, terutama karena memberikan kelebihan informasi terperinci – jauh lebih banyak daripada yang Anda miliki setelah menjalankan tes analisis deskriptif.
Informasi ini memberikan peneliti dan analis wawasan yang komprehensif ke dalam hubungan antara dua variabel. Ini juga dapat menunjukkan kesadaran terhadap sebab dan akibat dan prediksi mengenai tren dan pola di seluruh industri.
Plus, karena begitu banyak digunakan di dunia bisnis dan juga akademisi, ini adalah metode analisis statistik yang diterima secara universal.
Keterbatasan analisis inferensial
Ketika datang ke statistik inferensial, ada dua batasan utama.
Batasan pertama berasal dari fakta bahwa karena data yang dianalisis berasal dari populasi yang belum sepenuhnya diukur, analis data tidak akan pernah bisa 100% yakin bahwa statistik yang dihitung itu benar. Karena analisis inferensial didasarkan pada proses menggunakan nilai-nilai yang diukur dalam sampel untuk menyimpulkan nilai-nilai yang akan diukur dari total populasi, akan selalu ada beberapa tingkat ketidakpastian mengenai hasil.
Keterbatasan kedua adalah bahwa beberapa tes inferensial mengharuskan analis atau peneliti untuk membuat tebakan berdasarkan teori untuk menjalankan tes. Mirip dengan batasan pertama, akan ada ketidakpastian seputar tebakan ini, yang juga berarti beberapa dampak pada keandalan hasil beberapa uji statistik.
Jangan langsung mengambil kesimpulan
Sebelum Anda melompat ke kesimpulan yang berpotensi tidak akurat mengenai data, pastikan untuk memanfaatkan informasi yang menunggu dalam tes analisis inferensial.
Terlepas dari jenis kesimpulan yang ingin Anda dapatkan, atau hipotesis yang Anda mulai, Anda mungkin akan terkejut dengan hasil yang dapat dihasilkan oleh tes analisis inferensial.
Mencari perangkat lunak analisis statistik untuk menafsirkan semua set data Anda dengan lebih baik? Atau mungkin alat yang membuat analisis statistik yang paling rumit menjadi sederhana dan konklusif? Lihat daftar ulasan objektif kami di G2!
