Çıkarımsal Analiz ile Doğru Sonuca Ulaşın
Yayınlanan: 2020-03-23Hepimiz zaman zaman sonuçlara atlamaktan suçluyuz.
İster planlamak için çok uğraştığınız konferans için kimsenin bilet almayacağına, ister havaalanına iki saat önceden varmanın yeterli zaman olmadığına kendinizi ikna edin, hepimiz yaptık.
Günlük hayatımızın dışında, sektör ne olursa olsun iş yerinde yanlış sonuçlara atlamak kolaydır. Bunu yaptığımızda aslında genelleme yapıyoruz, peki ya bu genellemeleri daha doğru bir şekilde yapabilseydiniz? Çıkarımsal analiz testleri çalıştırdığınızda mümkündür.
Çıkarımsal analiz nedir?
Çıkarımsal analiz, bir popülasyon örneğinden toplanan bilgilere dayanan bir popülasyon hakkında sonuçların güvenilirliğini çıkarmak ve ölçmek için kullanılır. Çıkarımsal analiz bir popülasyondaki herkesi örneklemediğinden, sonuçlar her zaman bir miktar belirsizlik içerecektir.
İstatistiksel analize daldığımızda, çoğu zaman analiz etmek istediğimiz popülasyonun büyüklüğü çok büyüktür ve bu da herkesi incelemeyi imkansız hale getirir. Bu durumlarda, belirli bir popülasyondaki bireylerin rastgele örnekleri kullanılarak veriler toplanır. Ardından, genel popülasyon hakkında sonuçlara varmak için veriler üzerinde çıkarımsal analiz kullanılır.
Tüm bir insan popülasyonunu ölçmek çoğu zaman imkansız olduğundan, çıkarımsal analiz, popülasyon içindeki bir birey örneğinden veri toplamaya dayanır. Esasen, çıkarımsal analiz, popülasyonun ne düşünebileceğini veya gösterebileceğini bir veri örneğinden çıkarmaya çalışmak için kullanılır.
Bununla ilgili iki ana yol vardır:
- Parametreleri tahmin etme: Bir veri örneğinden (örnek ortalaması gibi) bir istatistik almak ve onu popülasyon (popülasyon ortalaması) hakkında bir sonuca varmak için kullanmak.
- Hipotez testleri: Belirli araştırma sorularını yanıtlamak için veri örneklerinin kullanılması.
Parametrelerin tahmininde, örneklem, bir güven aralığına ek olarak tüm popülasyonu tanımlayan bir değeri tahmin etmek için kullanılır. Ardından, tahmin oluşturulur.
Hipotez testinde veriler, bir varsayımı destekleyecek veya reddedecek kadar güçlü olup olmadığını belirlemek için kullanılır.
Tanımlayıcı analiz ve çıkarımsal analiz
İnsanların en sık kullandığı iki ana istatistiksel analiz türü, tanımlayıcı analiz ve çıkarımsal analizdir. Bu nedenle, veri analistlerine toplanan verilere farklı içgörüler sağlasalar da, ikisinin birbiriyle karıştırılması nadir değildir.
Resmin tamamı gösterilemese de, birlikte kullanıldıklarında, aynı veri kümesine dayandıkları için veri görselleştirme ve tahmin analitiği için güçlü bir araç sağlarlar.
Tanımlayıcı istatistiksel analiz , verileri bir şekilde açıklayan bilgiler verir. Bu bazen verilerin ne sunduğunu açıklamak için veri görselleştirme yazılımıyla yapılan çizelgeler ve grafiklerle yapılır. Bu istatistiksel analiz yöntemi, sonuçlar çıkarmak için kullanılmaz, yalnızca bilgileri özetlemek için kullanılır.
Çıkarımsal istatistiksel analiz , sonuçları çıkarmak için kullanılacak yöntemdir. Kullanıcıların, analiz edilen örneklere dayalı olarak daha büyük bir popülasyon hakkındaki eğilimleri çıkarmasına veya sonuçlandırmasına olanak tanır. Temel olarak, bir örneklemden veri alır ve daha sonra daha büyük bir popülasyon veya grup hakkında sonuçlar çıkarır.
Bu tür istatistiksel analiz, genellikle bir örnek içindeki değişkenler arasındaki ilişkiyi incelemek için kullanılır ve popülasyonu doğru bir şekilde temsil eden sonuçlara ve genellemelere izin verir. Ve tanımlayıcı analizden farklı olarak, işletmeler bir hipotezi test edebilir ve bu verilerden çeşitli sonuçlar çıkarabilir.

Bunu şöyle düşünelim. Bir beyzbol maçındasınız ve 100 hayran örneğine sosisli sandviç sevip sevmediklerini sorun. Tanımlayıcı bir analiz olan evet veya hayır yanıtlarından oluşan bir çubuk grafik oluşturabilirsiniz. Veya araştırmanızı, nüfusun %93'ünün (tüm beyzbol stadyumlarındaki tüm beyzbol taraftarlarının) sosisli sandviçleri sevdiği sonucuna varmak için kullanabilirsiniz, bu çıkarımsal bir analiz olacaktır.
Çıkarımsal analiz testleri türleri
İstatistik alanında yer alan birçok çıkarımsal analiz testi türü vardır. Hangisini kullanmayı seçeceğiniz, örneklem büyüklüğünüze, çözmeye çalıştığınız hipoteze ve test edilen popülasyonun büyüklüğüne bağlı olacaktır.
Doğrusal regresyon analizi
Doğrusal regresyon analizi, bir veri setindeki iki değişken (X ve Y) arasındaki ilişkiyi anlamak için, olaylar ve hedefler üzerinde geleceğe yönelik projeksiyonlar yapmak için bilinmeyen değişkeni tahmin etmenin bir yolu olarak kullanılır.
Regresyon analizinin temel amacı, bilinen (veya sabit) değişkenlerinizin (X ve Y) değerlerine dayalı olarak rastgele bir değişkenin (Z) değerlerini tahmin etmektir. Bu, tipik olarak, aşağıdaki gibi bir dağılım grafiği ile temsil edilir.
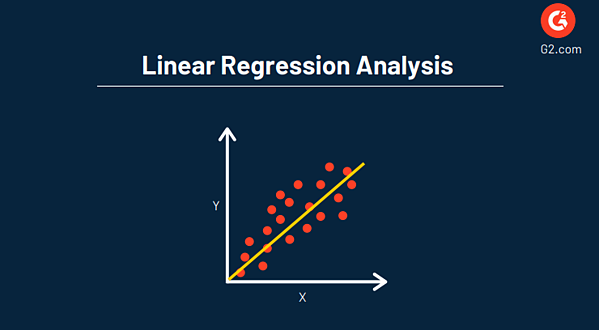
Analizinizde regresyon kullanmanın önemli bir avantajı, verilere ayrıntılı bir bakış sağlaması ve gelecekte tahmine dayalı analitik ve verileri optimize etmek için kullanılabilecek bir denklem içermesidir.
Regresyon analizi için formül:
Y = a + b(x)
A → y-kesişimini, x = 0 olduğunda y'nin değerini ifade eder.
B → eğimi veya koşunun üzerindeki yükselişi ifade eder
Korelasyon analizi
Bir diğer çıkarımsal analiz testi, iki değişkenin birbirine ne ölçüde bağımlı olduğunu anlamak için kullanılan korelasyon analizidir. Bu analiz esas olarak iki değişken arasındaki ilişkinin gücünü ve korelasyonlarının güçlü mü yoksa zayıf mı olduğunu test eder.
İki değişken arasındaki korelasyon, değişkenlere bağlı olarak negatif veya pozitif olabilir. Birindeki değişiklik diğerini etkilemediğinde, değişkenler "ilişkisiz" olarak kabul edilir.
Buna bir örnek fiyat ve talep olacaktır. Bunun nedeni, talepteki bir artışın fiyatta karşılık gelen bir artışa neden olmasıdır. Fiyat artacaktır çünkü daha fazla tüketici bir şey ister ve bunun için daha fazla ödemeye isteklidir.
Genel olarak, korelasyon analizinin amacı, iki değişken arasındaki ilişkiyi ve birlikte nasıl hareket ettiklerini gösteren sayısal değeri bulmaktır. Regresyon gibi, bu da genellikle bir grafik oluşturmak için veri görselleştirme yazılımı kullanılarak yapılır.
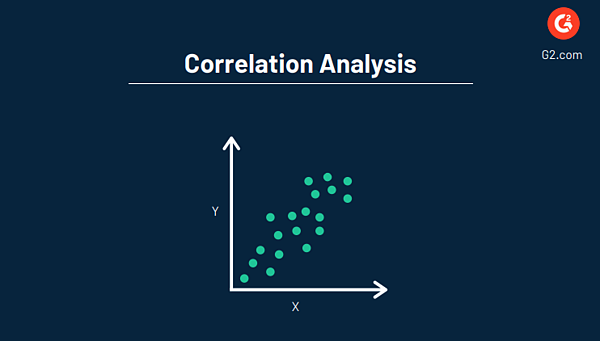
İlgili: Farklılıklar ve işletmenizin hangi yöntemi kullanması gerektiği de dahil olmak üzere, korelasyonlar ve regresyon arasındaki giriş ve çıkışlar hakkında daha fazla bilgi edinin.
varyans analizi
Varyans analizi (ANOVA) istatistiksel yöntemi, bir veri setinden iki veya daha fazla ortalama arasındaki farkları test etmek ve analiz etmek için kullanılır. Bu, numuneler arasındaki varyasyon miktarı incelenerek yapılır.
En basit ifadeyle, ANOVA, t-testini iki ortalama arasında genelleştirmeye ek olarak, iki veya daha fazla popülasyon ortalamasının eşit olup olmadığının istatistiksel bir testini sağlar.

Daha fazla bilgi edinin: İki grup arasındaki farkların ne kadar önemli olduğunu göstermek için bir t testi kullanılır. Esasen, farklılıkların (araçlar/ortalamalar olarak ölçülen) tesadüfen oluşup oluşmadığının anlaşılmasını sağlar.
Bu yöntem, grupların test edilmesinin aralarında bir fark olup olmadığını görmesine izin verecektir. Örneğin, bir lisenin diğerinden daha yüksek puan alıp almadığını görmek için aynı sınava giren iki farklı lisedeki öğrencileri test edebilirsiniz.
ANOVA ayrıca iki türe ayrılabilir:
- Tek yönlü: İki seviyeli yalnızca bir bağımsız değişken. Bir örnek, bir fıstık ezmesi markası olabilir.
- İki yönlü: Birden fazla seviyeye sahip olabilen iki bağımsız değişken. Bir örnek, bir marka fıstık ezmesi ve kalori olabilir.
Düzey, değişken içindeki farklı gruplardır. Dolayısıyla, yukarıdakiyle aynı örneği kullanarak, fıstık ezmesi markalarının seviyeleri Jif, Skippy veya Peter Pan olabilir. Kalori seviyeleri pürüzsüz, kremsi veya organik olabilir.
kovaryans analizi
Kovaryans analizi (ANCOVA), varyans analizi (ANOVA) ve regresyonun benzersiz bir karışımıdır. ANCOVA, diğerlerini etkilemeden bir seferde bir bağımsız değişken veya faktör göz önüne alındığında hangi ek bilgilerin mevcut olduğunu gösterebilir.
Sıklıkla kullanılır:
- Çoklu regresyon çizgilerini karşılaştırmanın bir yolu olarak çoklu regresyonun bir uzantısı için
- Çalışmanızın ana odağı olmayan değişkenleri (diğer değişkenleri) kontrol etmek için
- Varyans analizinin bir uzantısı için
- İlgilenilen diğer değişkenlerin kombinasyonlarını incelemek
- Randomize edilemeyen ancak ölçülebilen faktörleri kontrol etmek
ANCOVA, ortalamaya gerilemenin son test istatistik ölçümünüzü etkileyeceği durumlarda bir analizin ön testi veya son testi için de kullanılabilir.
Örnek olarak, işletmenizin halk için kan basıncını düşüren yeni ilaçlar ürettiğini varsayalım. Dört tedavi grubunu ve bir kontrol grubunu izleyen bir çalışma yürütebilirsiniz.
ANOVA kullanıyorsanız, tedavinin aslında kan basıncını düşürüp düşürmediğini anlayabilirsiniz. ANCOVA'yı dahil ettiğinizde, aile hayatı, meslek veya diğer reçeteli ilaç kullanımı gibi sonucu etkileyebilecek diğer faktörleri kontrol edebilirsiniz.
Güven aralığı
Güven aralığı, tüm popülasyonun bir parametresini, genellikle ortalamasını tahmin eden çıkarımsal analizde kullanılan bir araçtır. Esasen, belirli bir istatistikte ne kadar belirsizlik olduğudur ve genellikle bir hata payıyla kullanılır.
Güven aralığı, tüm popülasyonu araştırmak mümkün olsaydı, anket veya anket sonuçlarının beklediğiniz gibi olduğundan ne kadar emin olduğunuzu yansıtan bir sayı ile ifade edilir.
Örneğin, bir anket veya anketin sonuçları %98 güven aralığına sahipse, bu, popülasyon ortalamasını içeren %98 emin olabileceğiniz değer aralığını tanımlar. Bu sonuca varmak için üç parça bilgiye ihtiyaç vardır:
- Güven düzeyi : Bir örnekleme yöntemiyle ilişkili belirsizliği tanımlar
- İstatistik: Anket veya anketten toplanan veriler
- Hata payı : Sonuçlarınızın gerçek popülasyon değerinden ne kadar farklı olacağı
ki-kare testi
x2 testi olarak da bilinen bir ki-kare testi, tüm değişkenler nominal olduğunda (sayısal değeri olmayan değerlere sahip bir değişken olarak da bilinir), cinsiyet, maaş farkı, siyasi bağlantı vb.
Bu testler tipik olarak, gözlemleri ortak özelliklere göre gruplandıran belirli beklenmedik durum tablolarıyla birlikte kullanılır.
Ki-kare testinin cevaplayabileceği sorular şunlar olabilir:
- Amerika Birleşik Devletleri'ndeki tüm insanlar için eğitim düzeyi ve medeni durum ilişkili mi?
- Seçmen niyeti ile siyasi parti üyeliği arasında bir ilişki var mı?
- Cinsiyet, insanların hangi tatili tercih ettiğini etkiler mi?
Genellikle bu testler, potansiyel olarak doğru bir sonuca varmak için belirli bir örnekten veri toplamak için basit rastgele örnekleme adı verilen istatistiksel analiz yöntemi kullanılarak yapılır. Yukarıda listelenen ilk soruyu kullanırsak, veriler şöyle görünebilir:
| İsim | Durum | Eğitim | |
| 1 | Melisa | Boşanmış | Doktora veya üstü |
| 2 | Casey | Evli | Lisans |
| 3 | Angela | Evli | GED |
| 4 | Alyssa | dul | Lisans |
| 5 | Jenna | Hiç evlenmemiş | GED |
Bu beklenmedik durum tabloları, basit rastgele örnekleme yoluyla toplanan verileri düzenlemek için bir başlangıç noktası olarak kullanılır.
Çıkarımsal analizin avantajları
Çıkarımsal analiz kullanmanın birçok avantajı vardır, esas olarak ayrıntılı bilgi fazlası sağlar - tanımlayıcı bir analiz testi yaptıktan sonra sahip olacağınızdan çok daha fazlası.
Bu bilgi, araştırmacılara ve analistlere iki değişken arasındaki ilişkilere dair kapsamlı bilgiler sağlar. Ayrıca, endüstrilerdeki eğilimler ve kalıplarla ilgili neden-sonuç ve tahminlere yönelik farkındalık gösterebilir.
Ayrıca, iş dünyasında olduğu kadar akademide de çok yaygın olarak kullanıldığından, evrensel olarak kabul edilen bir istatistiksel analiz yöntemidir.
Çıkarımsal analizin sınırlamaları
Çıkarımsal istatistikler söz konusu olduğunda, iki ana sınırlama vardır.
İlk sınırlama, analiz edilen verilerin tam olarak ölçülmemiş bir popülasyondan olması nedeniyle, veri analistlerinin hesaplanan istatistiklerin doğruluğundan %100 emin olamamalarından kaynaklanmaktadır. Çıkarımsal analiz, toplam popülasyondan ölçülecek değerleri sonuçlandırmak için bir örnekte ölçülen değerleri kullanma sürecine dayandığından, sonuçlarla ilgili her zaman bir miktar belirsizlik olacaktır.
İkinci sınırlama, bazı çıkarımsal testlerin analistin veya araştırmacının testleri yürütmek için teorilere dayalı eğitimli bir tahminde bulunmasını gerektirmesidir. İlk sınırlamaya benzer şekilde, bu tahminleri çevreleyen belirsizlik olacaktır, bu da bazı istatistiksel testlerin sonuçlarının güvenilirliği üzerinde bazı yansımalar anlamına gelecektir.
Sonuçlara atlamayın
Verilerle ilgili potansiyel olarak yanlış bir sonuca varmadan önce, çıkarımsal bir analiz testinde sizi bekleyen bilgilerden yararlandığınızdan emin olun.
Varmak istediğiniz sonucun türü veya başladığınız hipotez ne olursa olsun, bir çıkarımsal analiz testinin getirebileceği sonuçlara şaşırabilirsiniz.
Tüm veri kümelerinizi daha iyi yorumlamak için istatistiksel analiz yazılımı mı arıyorsunuz ? Ya da belki de en karmaşık istatistiksel analizi bile basit ve kesin hale getiren bir araç? G2'deki tarafsız incelemeler listemize göz atın!
