มาสู่ข้อสรุปที่ถูกต้องด้วยการวิเคราะห์เชิงอนุมาน
เผยแพร่แล้ว: 2020-03-23เราทุกคนต่างมีความผิดในการด่วนสรุปเป็นระยะๆ
ไม่ว่าจะเป็นการโน้มน้าวตัวเองว่าจะไม่มีใครซื้อตั๋วสำหรับการประชุมที่คุณทำงานหนักเพื่อวางแผน หรือมาถึงสนามบินล่วงหน้าสองชั่วโมงก็ไม่มีเวลาเพียงพอ เราทุกคนก็ทำเสร็จแล้ว
นอกชีวิตประจำวันของเรา เป็นเรื่องง่ายที่จะข้ามไปยังข้อสรุปที่ไม่ถูกต้องในที่ทำงาน ไม่ว่าจะเป็นอุตสาหกรรมใดก็ตาม เมื่อเราทำเช่นนี้ เรากำลังสรุปโดยทั่วไป แต่ถ้าคุณสามารถสร้างลักษณะทั่วไปเหล่านี้ได้แม่นยำยิ่งขึ้นล่ะ เป็นไปได้เมื่อคุณเรียกใช้การทดสอบการวิเคราะห์เชิงอนุมาน
การวิเคราะห์เชิงอนุมานคืออะไร?
การวิเคราะห์เชิงอนุมานใช้เพื่อวาดและวัดความน่าเชื่อถือของข้อสรุปเกี่ยวกับประชากรที่ยึดตามข้อมูลที่รวบรวมจากกลุ่มตัวอย่างของประชากร เนื่องจากการวิเคราะห์เชิงอนุมานไม่ได้สุ่มตัวอย่างทุกคนในประชากร ผลลัพธ์จึงมักมีความไม่แน่นอนอยู่บ้าง
เมื่อเจาะลึกลงไปในการวิเคราะห์ทางสถิติ บ่อยครั้งที่ขนาดของประชากรที่เราต้องการจะวิเคราะห์นั้นใหญ่เกินไป ทำให้ไม่สามารถศึกษาทุกคนได้ ในกรณีเหล่านี้ ข้อมูลจะถูกเก็บรวบรวมโดยใช้ตัวอย่างสุ่มของบุคคลภายในกลุ่มประชากรเฉพาะ จากนั้นจึงใช้การวิเคราะห์เชิงอนุมานกับข้อมูลเพื่อหาข้อสรุปเกี่ยวกับประชากรโดยรวม
เนื่องจากมักเป็นไปไม่ได้ที่จะวัดจำนวนประชากรทั้งหมด การวิเคราะห์เชิงอนุมานจึงอาศัยการรวบรวมข้อมูลจากกลุ่มตัวอย่างของบุคคลภายในประชากร โดยพื้นฐานแล้ว การวิเคราะห์เชิงอนุมานจะใช้เพื่อพยายาม อนุมาน จากตัวอย่างข้อมูลที่ประชากรอาจคิดหรือแสดง
มีสองวิธีหลักในการดำเนินการนี้:
- การประมาณค่าพารามิเตอร์: นำสถิติจากตัวอย่างข้อมูล (เช่น ค่าเฉลี่ยตัวอย่าง) มาใช้สรุปข้อมูลบางอย่างเกี่ยวกับประชากร (ค่าเฉลี่ยประชากร)
- การทดสอบสมมติฐาน: การใช้ตัวอย่างข้อมูลเพื่อตอบคำถามการวิจัยที่เฉพาะเจาะจง
ในการประมาณค่าพารามิเตอร์ กลุ่มตัวอย่างใช้เพื่อประมาณค่าที่อธิบายประชากรทั้งหมด นอกเหนือจากช่วงความเชื่อมั่น จากนั้น ค่าประมาณจะถูกสร้างขึ้น
ในการทดสอบสมมติฐาน ข้อมูลจะถูกใช้เพื่อระบุว่ามีความแข็งแกร่งเพียงพอที่จะสนับสนุนหรือปฏิเสธสมมติฐานหรือไม่
การวิเคราะห์เชิงพรรณนากับการวิเคราะห์เชิงอนุมาน
การวิเคราะห์ทางสถิติสองประเภทหลักที่ผู้คนใช้บ่อยที่สุดคือการวิเคราะห์เชิงพรรณนาและการวิเคราะห์เชิงอนุมาน ด้วยเหตุนี้ จึงไม่ใช่เรื่องแปลกที่ทั้งสองจะสับสนกัน แม้ว่าพวกเขาจะให้ข้อมูลเชิงลึกที่แตกต่างกันในข้อมูลที่รวบรวมมาแก่นักวิเคราะห์ข้อมูล
แม้ว่าจะไม่สามารถแสดงภาพรวมทั้งหมดได้ แต่เมื่อใช้งานร่วมกัน จะมอบเครื่องมือที่มีประสิทธิภาพในการแสดงข้อมูลเป็นภาพและการวิเคราะห์การคาดการณ์ เนื่องจากต้องใช้ชุดข้อมูลชุดเดียวกัน
การวิเคราะห์ทางสถิติเชิงพรรณนา ให้ข้อมูลที่อธิบายข้อมูลในทางใดทางหนึ่ง บางครั้งใช้แผนภูมิและกราฟที่สร้างด้วยซอฟต์แวร์การแสดงข้อมูลเพื่ออธิบายสิ่งที่ข้อมูลนำเสนอ วิธีการวิเคราะห์ทางสถิตินี้ไม่ได้ใช้เพื่อสรุปผล เพียงเพื่อสรุปข้อมูลเท่านั้น
การวิเคราะห์ทางสถิติเชิงอนุมาน เป็นวิธีการที่จะใช้ในการสรุปผล อนุญาตให้ผู้ใช้อนุมานหรือสรุปแนวโน้มเกี่ยวกับประชากรจำนวนมากขึ้นตามตัวอย่างที่วิเคราะห์ โดยพื้นฐานแล้วจะใช้ข้อมูลจากกลุ่มตัวอย่างแล้วทำการสรุปเกี่ยวกับประชากรหรือกลุ่มที่ใหญ่ขึ้น
การวิเคราะห์ทางสถิติประเภทนี้มักใช้เพื่อศึกษาความสัมพันธ์ระหว่างตัวแปรภายในกลุ่มตัวอย่าง เพื่อให้สามารถสรุปและสรุปข้อมูลที่แสดงถึงประชากรได้อย่างแม่นยำ และต่างจากการวิเคราะห์เชิงพรรณนา ธุรกิจสามารถทดสอบสมมติฐานและได้ข้อสรุปต่างๆ จากข้อมูลนี้

ลองคิดแบบนี้ คุณอยู่ที่การแข่งขันเบสบอลและถามแฟน ๆ 100 ตัวอย่างว่าพวกเขาชอบฮอทดอกหรือไม่ คุณสามารถสร้างกราฟแท่งของคำตอบใช่หรือไม่ใช่ ซึ่งจะเป็นการวิเคราะห์เชิงพรรณนา หรือคุณอาจใช้งานวิจัยของคุณเพื่อสรุปว่า 93% ของประชากร (แฟนเบสบอลทุกคนในสนามเบสบอลทั้งหมด) ชอบฮอทดอก ซึ่งจะเป็นการวิเคราะห์เชิงอนุมาน
ประเภทของการทดสอบการวิเคราะห์เชิงอนุมาน
มีการทดสอบการวิเคราะห์เชิงอนุมานหลายประเภทที่อยู่ในฟิลด์สถิติ ข้อใดที่คุณเลือกใช้จะขึ้นอยู่กับขนาดกลุ่มตัวอย่าง สมมติฐานที่คุณกำลังพยายามแก้ และขนาดของประชากรที่กำลังทดสอบ
การวิเคราะห์การถดถอยเชิงเส้น
การวิเคราะห์การถดถอยเชิงเส้นใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัว (X และ Y) ในชุดข้อมูลเพื่อเป็นการประมาณค่าตัวแปรที่ไม่รู้จักเพื่อคาดการณ์เหตุการณ์และเป้าหมายในอนาคต
วัตถุประสงค์หลักของการวิเคราะห์การถดถอยคือการประมาณค่าของตัวแปรสุ่ม (Z) ตามค่าของตัวแปรที่ทราบ (หรือคงที่) (X และ Y) โดยทั่วไปจะแสดงด้วยแผนภาพแบบกระจาย ดังตัวอย่างด้านล่าง
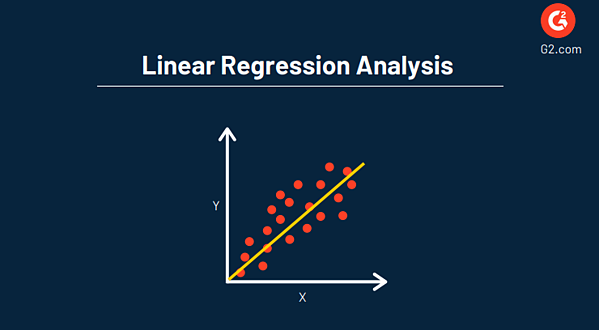
ข้อได้เปรียบที่สำคัญอย่างหนึ่งของการใช้การถดถอยในการวิเคราะห์ของคุณคือ ให้ข้อมูลโดยละเอียดและรวมถึงสมการที่สามารถใช้สำหรับการวิเคราะห์เชิงคาดการณ์และเพิ่มประสิทธิภาพข้อมูลในอนาคต
สูตรสำหรับการวิเคราะห์การถดถอยคือ:
Y = a + b(x)
A → หมายถึงจุดตัด y ค่าของ y เมื่อ x = 0
B → หมายถึงความชันหรือขึ้นเหนือการวิ่ง
การวิเคราะห์สหสัมพันธ์
การทดสอบการวิเคราะห์เชิงอนุมานอีกแบบหนึ่งคือการวิเคราะห์สหสัมพันธ์ ซึ่งใช้เพื่อทำความเข้าใจขอบเขตที่ตัวแปรสองตัวพึ่งพากันและกัน การวิเคราะห์นี้จะทดสอบความแข็งแกร่งของความสัมพันธ์ระหว่างตัวแปรสองตัว และความสัมพันธ์ของตัวแปรทั้งสองนั้นแข็งแกร่งหรืออ่อนแอ
ความสัมพันธ์ระหว่างสองตัวแปรอาจเป็นค่าลบหรือค่าบวกก็ได้ ขึ้นอยู่กับตัวแปร ตัวแปรจะถือว่า "ไม่สัมพันธ์กัน" เมื่อการเปลี่ยนแปลงในตัวแปรหนึ่งไม่ส่งผลต่ออีกตัวแปรหนึ่ง
ตัวอย่างนี้จะเป็นราคาและอุปสงค์ เนื่องจากความต้องการที่เพิ่มขึ้นทำให้ราคาเพิ่มขึ้นตามไปด้วย ราคาจะเพิ่มขึ้นเพราะผู้บริโภคต้องการบางสิ่งบางอย่างมากขึ้นและเต็มใจที่จะจ่ายมากขึ้น
โดยรวมแล้ว วัตถุประสงค์ของการวิเคราะห์สหสัมพันธ์คือการหาค่าตัวเลขที่แสดงความสัมพันธ์ระหว่างตัวแปรทั้งสองและวิธีที่พวกมันเคลื่อนที่ไปด้วยกัน เช่นเดียวกับการถดถอย โดยทั่วไปจะทำโดยใช้ซอฟต์แวร์การแสดงข้อมูลเพื่อสร้างกราฟ
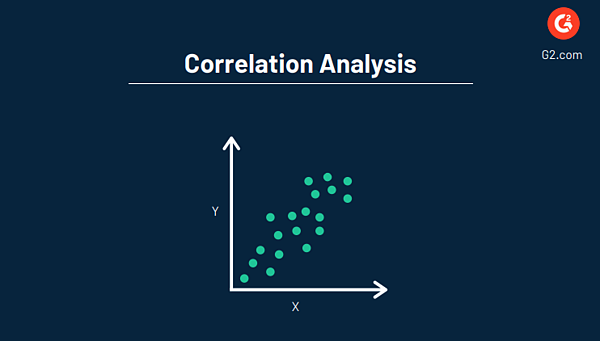
ที่เกี่ยวข้อง: เรียนรู้เพิ่มเติมเกี่ยวกับความสัมพันธ์ที่ลึกซึ้งกับการถดถอย รวมถึงความแตกต่างและวิธีการที่ธุรกิจของคุณควรใช้
การวิเคราะห์ความแปรปรวน
วิธีทางสถิติการวิเคราะห์ความแปรปรวน (ANOVA) ใช้เพื่อทดสอบและวิเคราะห์ความแตกต่างระหว่างสอง วิธี หรือมากกว่าจากชุดข้อมูล ทำได้โดยการตรวจสอบปริมาณความแปรผันระหว่างตัวอย่าง
ในแง่ที่ง่ายที่สุด ANOVA ให้การทดสอบทางสถิติว่าค่าเฉลี่ยประชากรสองค่าเท่ากันหรือไม่ นอกเหนือจากการสรุปการทดสอบ t ระหว่างสองวิธี

เรียนรู้เพิ่มเติม: การทดสอบ t ใช้เพื่อแสดงว่าความแตกต่างระหว่างสองกลุ่มมีความสำคัญเพียงใด โดยพื้นฐานแล้ว จะช่วยให้เข้าใจว่าความแตกต่าง (วัดด้วยค่าเฉลี่ย/ค่าเฉลี่ย) อาจเกิดขึ้นโดยบังเอิญหรือไม่
วิธีนี้จะอนุญาตให้ทดสอบกลุ่มเพื่อดูว่ามีความแตกต่างระหว่างพวกเขาหรือไม่ ตัวอย่างเช่น คุณอาจทดสอบนักเรียนในโรงเรียนมัธยมศึกษาตอนปลายสองแห่งที่แตกต่างกันซึ่งทำข้อสอบเดียวกันเพื่อดูว่าโรงเรียนมัธยมแห่งหนึ่งมีคะแนนสูงกว่าที่อื่นหรือไม่
ANOVA สามารถแบ่งออกเป็นสองประเภท:
- ทางเดียว: ตัวแปรอิสระเพียงตัวเดียวที่มีสองระดับ ตัวอย่างจะเป็นยี่ห้อของเนยถั่ว
- สองทาง: ตัวแปรอิสระสองตัวที่สามารถมีหลายระดับได้ ตัวอย่างจะเป็นยี่ห้อของเนยถั่วและแคลอรี่
ระดับเป็นเพียงกลุ่มต่างๆ ภายในตัวแปร จากตัวอย่างเดียวกันกับข้างต้น ระดับของเนยถั่วอาจเป็นยี่ห้อ Jif, Skippy หรือ Peter Pan ระดับแคลอรี่อาจเป็นแบบเรียบ แบบครีม หรือแบบออร์แกนิก
การวิเคราะห์ความแปรปรวนร่วม
การวิเคราะห์ความแปรปรวนร่วม (ANCOVA) เป็นการผสมผสานระหว่างการวิเคราะห์ความแปรปรวน (ANOVA) และการถดถอยที่ไม่เหมือนใคร ANCOVA สามารถแสดงข้อมูลเพิ่มเติมว่ามีอะไรบ้างเมื่อพิจารณาตัวแปรหรือปัจจัยอิสระหนึ่งตัวในแต่ละครั้ง โดยไม่กระทบต่อผู้อื่น
มักใช้:
- สำหรับการขยายการถดถอยพหุคูณเพื่อเปรียบเทียบเส้นถดถอยหลายเส้น
- เพื่อควบคุม covariates (ตัวแปรอื่นๆ) ที่ไม่ใช่จุดสนใจหลักของการศึกษาของคุณ
- สำหรับการขยายการวิเคราะห์ความแปรปรวน
- เพื่อศึกษาชุดค่าผสมของตัวแปรอื่นๆ ที่น่าสนใจ
- เพื่อควบคุมปัจจัยที่ไม่สามารถสุ่มได้ แต่วัดได้
ANCOVA ยังสามารถใช้เพื่อทดสอบก่อนหรือหลังการทดสอบ เมื่อการถดถอยไปยังค่าเฉลี่ยจะส่งผลต่อการวัดสถิติหลังการทดสอบของคุณ
ตัวอย่างเช่น สมมติว่าธุรกิจของคุณสร้างเภสัชภัณฑ์ใหม่ๆ ให้กับประชาชนซึ่งช่วยลดความดันโลหิตได้ คุณอาจทำการศึกษาที่เฝ้าติดตามกลุ่มการรักษาสี่กลุ่มและกลุ่มควบคุมหนึ่งกลุ่ม
หากคุณใช้ ANOVA คุณจะสามารถบอกได้ว่าการรักษานั้นช่วยลดความดันโลหิตได้จริงหรือไม่ เมื่อคุณรวม ANCOVA คุณสามารถควบคุมปัจจัยอื่นๆ ที่อาจส่งผลต่อผลลัพธ์ เช่น ชีวิตครอบครัว อาชีพ หรือการใช้ยาที่ต้องสั่งโดยแพทย์อื่นๆ
ช่วงความเชื่อมั่น
ช่วงความเชื่อมั่นเป็นเครื่องมือที่ใช้ในการวิเคราะห์เชิงอนุมานที่ประมาณค่าพารามิเตอร์ ซึ่งมักจะเป็นค่าเฉลี่ยของประชากรทั้งหมด โดยพื้นฐานแล้ว มันคือความไม่แน่นอนที่มีกับสถิติเฉพาะใดๆ และมักใช้กับส่วนต่างของข้อผิดพลาด
ช่วงความเชื่อมั่นจะแสดงด้วยตัวเลขที่สะท้อนว่าคุณมั่นใจแค่ไหนว่าผลลัพธ์ของการสำรวจหรือการสำรวจนั้นเป็นสิ่งที่คุณคาดหวังหากสามารถสำรวจประชากรทั้งหมดได้
ตัวอย่างเช่น หากผลลัพธ์ของโพลหรือแบบสำรวจมีช่วงความเชื่อมั่น 98% ค่านี้จะกำหนดช่วงของค่าที่คุณสามารถระบุได้ 98% ว่ามีค่าเฉลี่ยประชากร ในการสรุปนี้ จำเป็นต้องมีข้อมูลสามส่วน:
- ระดับความเชื่อมั่น : อธิบายความไม่แน่นอนที่เกี่ยวข้องกับวิธีการสุ่มตัวอย่าง
- สถิติ: ข้อมูลที่รวบรวมจากการสำรวจหรือโพล
- Margin of error : ผลลัพธ์ของคุณจะแตกต่างจากมูลค่าประชากรจริงกี่เปอร์เซ็นต์
การทดสอบไคสแควร์
การทดสอบไคสแควร์ หรือที่เรียกว่าการทดสอบ x2 ใช้เพื่อระบุความแตกต่างระหว่างกลุ่มเมื่อตัวแปรทั้งหมดเป็นค่าที่ระบุ (เรียกอีกอย่างว่าตัวแปรที่มีค่าที่ไม่มีค่าตัวเลข) เช่น เพศ ช่องว่างเงินเดือน ความเกี่ยวพันทางการเมือง และอื่นๆ
การทดสอบเหล่านี้มักใช้กับตารางฉุกเฉินเฉพาะที่จัดกลุ่มการสังเกตตามลักษณะทั่วไป
คำถามที่การทดสอบไคสแควร์สามารถตอบได้อาจเป็น:
- ระดับการศึกษาและสถานภาพการสมรสเกี่ยวข้องกับทุกคนในสหรัฐอเมริกาหรือไม่?
- มีความสัมพันธ์ระหว่างเจตนาของผู้มีสิทธิเลือกตั้งกับการเป็นสมาชิกพรรคการเมืองหรือไม่?
- เพศมีผลต่อวันหยุดที่ผู้คนชื่นชอบหรือไม่?
โดยปกติ การทดสอบเหล่านี้จะทำโดยใช้วิธีการวิเคราะห์ทางสถิติที่เรียกว่าการสุ่มตัวอย่างอย่างง่าย เพื่อรวบรวมข้อมูลจากกลุ่มตัวอย่างเฉพาะเพื่อให้ได้ข้อสรุปที่ถูกต้อง หากเราใช้คำถามแรกในรายการข้างต้น ข้อมูลอาจมีลักษณะดังนี้:
| ชื่อ | สถานะ | การศึกษา | |
| 1 | เมลิสสา | หย่าร้าง | ปริญญาเอกหรือสูงกว่า |
| 2 | เคซี่ย์ | แต่งงานแล้ว | ปริญญาตรี |
| 3 | แองเจล่า | แต่งงานแล้ว | GED |
| 4 | อลิสสา | หม้าย | ปริญญาตรี |
| 5 | เจนน่า | ไม่เคยแต่งงาน | GED |
ตารางฉุกเฉินเหล่านี้ใช้เป็นจุดเริ่มต้นในการจัดระเบียบข้อมูลที่รวบรวมผ่านการสุ่มตัวอย่างอย่างง่าย
ข้อดีของการวิเคราะห์เชิงอนุมาน
มีข้อดีหลายประการในการใช้การวิเคราะห์เชิงอนุมาน โดยหลักแล้วมันให้ข้อมูลรายละเอียดส่วนเกิน ซึ่งมากกว่าที่คุณจะมีหลังจากทำการทดสอบการวิเคราะห์เชิงพรรณนา
ข้อมูลนี้ช่วยให้นักวิจัยและนักวิเคราะห์มีความเข้าใจอย่างลึกซึ้งเกี่ยวกับความสัมพันธ์ระหว่างสองตัวแปร นอกจากนี้ยังสามารถแสดงความตระหนักต่อสาเหตุและผลกระทบและการคาดการณ์เกี่ยวกับแนวโน้มและรูปแบบทั่วทั้งอุตสาหกรรม
นอกจากนี้ เนื่องจากมีการใช้กันอย่างแพร่หลายในโลกธุรกิจและสถาบันการศึกษา จึงเป็นวิธีการวิเคราะห์ทางสถิติที่เป็นที่ยอมรับในระดับสากล
ข้อจำกัดของการวิเคราะห์เชิงอนุมาน
เมื่อพูดถึงสถิติอนุมาน มีข้อจำกัดหลักสองประการ
ข้อจำกัดแรกมาจากข้อเท็จจริงที่ว่าเนื่องจากข้อมูลที่กำลังวิเคราะห์มาจากประชากรที่ยังไม่ได้รับการวัดอย่างสมบูรณ์ นักวิเคราะห์ข้อมูลจึงไม่สามารถแน่ใจได้ 100% ว่าสถิติที่คำนวณนั้นถูกต้อง เนื่องจากการวิเคราะห์เชิงอนุมานอิงตามกระบวนการของการใช้ค่าที่วัดในตัวอย่างเพื่อสรุปค่าที่จะวัดจากประชากรทั้งหมด จึงมีความไม่แน่นอนในระดับหนึ่งเกี่ยวกับผลลัพธ์
ข้อ จำกัด ที่สองคือการทดสอบเชิงอนุมานบางอย่างต้องการให้นักวิเคราะห์หรือนักวิจัยทำการเดาอย่างมีการศึกษาตามทฤษฎีเพื่อทำการทดสอบ คล้ายกับข้อจำกัดแรก จะมีความไม่แน่นอนอยู่รอบๆ การเดาเหล่านี้ ซึ่งอาจหมายถึงผลกระทบบางประการต่อความน่าเชื่อถือของผลการทดสอบทางสถิติบางอย่าง
อย่าด่วนสรุป
ก่อนที่คุณจะข้ามไปยังข้อสรุปที่อาจไม่ถูกต้องเกี่ยวกับข้อมูล อย่าลืมใช้ประโยชน์จากข้อมูลที่รออยู่ในการทดสอบการวิเคราะห์เชิงอนุมาน
ไม่ว่าคุณจะต้องการสรุปประเภทใด หรือตั้งสมมติฐานไว้อย่างไร คุณอาจแปลกใจกับผลลัพธ์ที่ได้จากการทดสอบการวิเคราะห์เชิงอนุมาน
กำลังมองหา ซอฟต์แวร์การวิเคราะห์ทางสถิติ เพื่อตีความชุดข้อมูลทั้งหมดของคุณให้ดีขึ้นใช่หรือไม่ หรืออาจเป็นเครื่องมือที่ทำให้การวิเคราะห์ทางสถิติที่ซับซ้อนที่สุดเป็นเรื่องง่ายและสรุปได้ ตรวจสอบรายชื่อบทวิจารณ์ที่เป็นกลางใน G2!
