Приходите к правильному выводу с помощью логического анализа
Опубликовано: 2020-03-23Мы все виноваты в том, что время от времени делаем поспешные выводы.
Будь то убеждение себя в том, что никто не купит билет на конференцию, которую вы так усердно планировали, или в том, что прибыть в аэропорт за два часа просто недостаточно, мы все это делали.
Вне нашей повседневной жизни легко сделать неточные выводы на работе, независимо от отрасли. Когда мы делаем это, мы, по сути, обобщаем, но что, если бы вы могли сделать эти обобщения более точными? Это возможно, когда вы запускаете тесты логического анализа.
Что такое выводной анализ?
Логический анализ используется для получения и измерения надежности выводов о совокупности, основанных на информации, собранной из выборки совокупности. Поскольку логический анализ не отбирает всех в популяции, результаты всегда будут содержать некоторый уровень неопределенности.
Когда мы погружаемся в статистический анализ, часто размер совокупности, которую мы хотим проанализировать, слишком велик, что делает невозможным изучение всех. В этих случаях данные собираются с использованием случайных выборок лиц из определенной популяции. Затем на данных используется логический анализ, чтобы сделать выводы об общей совокупности.
Поскольку часто невозможно измерить всю популяцию людей, логический анализ основан на сборе данных из выборки людей в популяции. По сути, логический анализ используется, чтобы попытаться сделать вывод из выборки данных о том, что население может подумать или показать.
Есть два основных способа сделать это:
- Оценка параметров: получение статистики из выборки данных (например, среднего значения выборки) и использование ее для заключения о населении (среднее значение совокупности).
- Проверка гипотез: использование выборки данных для ответа на конкретные вопросы исследования.
При оценке параметров выборка используется для оценки значения, описывающего всю совокупность, в дополнение к доверительному интервалу. Затем составляется смета.
При проверке гипотез данные используются для определения того, достаточно ли они убедительны, чтобы подтвердить или отвергнуть предположение.
Описательный анализ против логического анализа
Двумя основными типами статистического анализа, которые люди используют чаще всего, являются описательный анализ и логический анализ. Из-за этого их нередко путают друг с другом, даже несмотря на то, что они дают аналитикам данных различное представление о собираемых данных.
Хотя невозможно показать всю картину, при совместном использовании они представляют собой мощный инструмент для визуализации данных и прогнозной аналитики, поскольку они основаны на одном и том же наборе данных.
Описательный статистический анализ дает информацию, которая каким-то образом описывает данные. Иногда это делается с помощью диаграмм и графиков, созданных с помощью программного обеспечения для визуализации данных, чтобы объяснить, что представляют собой данные. Этот метод статистического анализа используется не для выводов, а только для обобщения информации.
Выводной статистический анализ - это метод, который будет использоваться для получения выводов. Это позволяет пользователям делать выводы или делать выводы о тенденциях в отношении большей совокупности на основе анализируемых выборок. По сути, он берет данные из выборки, а затем делает выводы о большей совокупности или группе.
Этот тип статистического анализа часто используется для изучения взаимосвязи между переменными в выборке, что позволяет делать выводы и делать обобщения, точно отражающие генеральную совокупность. И в отличие от описательного анализа, бизнес может проверить гипотезу и сделать различные выводы на основе этих данных.

Давайте думать об этом таким образом. Вы находитесь на бейсбольном матче и спрашиваете выборку из 100 болельщиков, любят ли они хот-доги. Вы можете сделать гистограмму ответов «да» или «нет», что будет описательным анализом. Или вы могли бы использовать свое исследование, чтобы сделать вывод, что 93% населения (все фанаты бейсбола на всех бейсбольных стадионах) любят хот-доги, что было бы логическим выводом.
Типы тестов логического анализа
Есть много типов тестов логического анализа, которые находятся в области статистики. Какой из них вы решите использовать, будет зависеть от размера вашей выборки, гипотезы, которую вы пытаетесь решить, и размера тестируемой популяции.
Линейный регрессионный анализ
Линейный регрессионный анализ используется для понимания взаимосвязи между двумя переменными (X и Y) в наборе данных как способ оценки неизвестной переменной для прогнозирования будущих событий и целей.
Основная цель регрессионного анализа — оценить значения случайной величины (Z) на основе значений ваших известных (или фиксированных) переменных (X и Y). Обычно это представлено графиком рассеяния, как показано ниже.
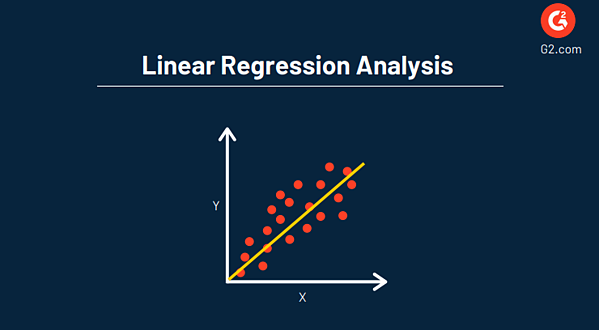
Одним из ключевых преимуществ использования регрессии в вашем анализе является то, что она обеспечивает подробный взгляд на данные и включает уравнение, которое можно использовать для прогнозной аналитики и оптимизации данных в будущем.
Формула регрессионного анализа:
Y = а + б (х)
A → относится к y-перехвату, значению y, когда x = 0
B → относится к уклону или подъему над трассой
Корреляционный анализ
Еще одним тестом логического анализа является корреляционный анализ, который используется для понимания того, в какой степени две переменные зависят друг от друга. Этот анализ по существу проверяет силу связи между двумя переменными, а также является ли их корреляция сильной или слабой.
Корреляция между двумя переменными также может быть отрицательной или положительной, в зависимости от переменных. Переменные считаются «некоррелированными», когда изменение одной не влияет на другую.
Примером этого может быть цена и спрос. Это связано с тем, что увеличение спроса вызывает соответствующее увеличение цены. Цена увеличится, потому что больше потребителей хотят чего-то и готовы платить за это больше.
В целом цель корреляционного анализа состоит в том, чтобы найти числовое значение, которое показывает взаимосвязь между двумя переменными и то, как они движутся вместе. Как и регрессия, это обычно делается с помощью программного обеспечения для визуализации данных для создания графика.
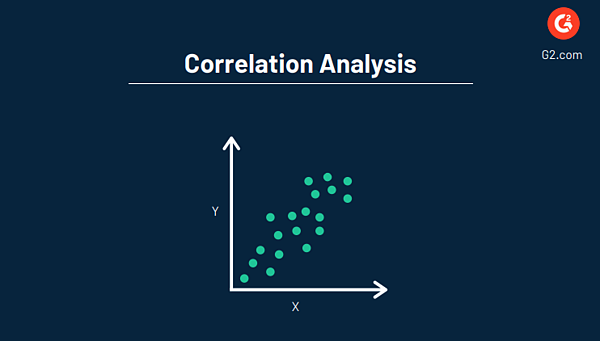
Связано: узнайте больше о плюсах и минусах корреляции и регрессии, в том числе о различиях и о том, какой метод должен использовать ваш бизнес.
Дисперсионный анализ
Статистический метод дисперсионного анализа (ANOVA) используется для проверки и анализа различий между двумя или более средними значениями из набора данных. Это делается путем изучения количества вариаций между образцами.
Проще говоря, ANOVA обеспечивает статистическую проверку равенства двух или более средних значений совокупности в дополнение к обобщению t-теста между двумя средними значениями.
Подробнее: t-критерий используется, чтобы показать, насколько значительны различия между двумя группами. По сути, это позволяет понять, могли ли различия (измеряемые в средних/средних значениях) возникнуть случайно.

Этот метод позволит протестировать группы, чтобы увидеть, есть ли между ними разница. Например, вы можете протестировать учащихся двух разных средних школ, которые сдают один и тот же экзамен, чтобы увидеть, выше ли тест одной средней школы по сравнению с другой.
ANOVA также можно разделить на два типа:
- Односторонний: Только одна независимая переменная с двумя уровнями. Примером может служить марка арахисового масла.
- Двусторонний: две независимые переменные, которые могут иметь несколько уровней. Примером может служить марка арахисового масла и калории.
Уровень — это просто разные группы внутри переменной. Итак, используя тот же пример, что и выше, уровни брендов арахисового масла могут быть Jif, Skippy или Peter Pan. Уровни калорий могут быть гладкими, сливочными или органическими.
Анализ ковариации
Ковариационный анализ (ANCOVA) представляет собой уникальное сочетание дисперсионного анализа (ANOVA) и регрессии. ANCOVA может показать, какая дополнительная информация доступна при одновременном рассмотрении одной независимой переменной или фактора, не влияя на другие.
Он часто используется:
- Для расширения множественной регрессии как способа сравнения множественных линий регрессии
- Чтобы контролировать ковариаты (другие переменные), которые не являются основным предметом вашего исследования
- Для расширения дисперсионного анализа
- Для изучения комбинаций других переменных, представляющих интерес
- Для контроля факторов, которые нельзя рандомизировать, но которые можно измерить
ANCOVA также можно использовать для предварительного или последующего тестирования анализа, когда регрессия к среднему повлияет на послетестовое измерение статистики.
В качестве примера предположим, что ваш бизнес создает новые лекарственные препараты для населения, которые снижают кровяное давление. Вы можете провести исследование, в котором отслеживаются четыре экспериментальные группы и одна контрольная группа.
Если вы используете ANOVA, вы сможете сказать, действительно ли лечение снижает кровяное давление. Когда вы включаете ANCOVA, вы можете контролировать другие факторы, которые могут повлиять на результат, такие как семейная жизнь, профессия или употребление других лекарств, отпускаемых по рецепту.
Доверительный интервал
Доверительный интервал — это инструмент, который используется в логическом анализе, который оценивает параметр, обычно среднее, для всей совокупности. По сути, это степень неопределенности в любой конкретной статистике, и обычно она используется с погрешностью.
Доверительный интервал выражается числом, которое отражает, насколько вы уверены, что результаты опроса или опроса соответствуют вашим ожиданиям, если бы было возможно опросить все население.
Например, если результаты опроса или опроса имеют доверительный интервал 98%, то это определяет диапазон значений, в котором вы можете быть уверены на 98%, что они содержат среднее значение генеральной совокупности. Чтобы прийти к такому выводу, необходимы три части информации:
- Уровень достоверности : описывает неопределенность, связанную с методом отбора проб.
- Статистика: данные, собранные в ходе опроса или опроса.
- Погрешность: на сколько процентных пунктов ваши результаты будут отличаться от реального значения населения.
критерий хи-квадрат
Тест хи-квадрат, также известный как тест x2, используется для выявления различий между группами, когда все переменные являются номинальными (также известными как переменные со значениями, которые не имеют числового значения), например пол, разница в зарплате, политическая принадлежность и т.д.
Эти тесты обычно используются с определенными таблицами непредвиденных обстоятельств, которые группируют наблюдения на основе общих характеристик.
Вопросы, на которые может ответить тест хи-квадрат, могут быть следующими:
- Связаны ли уровень образования и семейное положение для всех людей в Соединенных Штатах?
- Есть ли связь между намерениями избирателя и членством в политической партии?
- Влияет ли пол на то, какой праздник предпочитают люди?
Обычно эти тесты проводятся с использованием метода статистического анализа, называемого простой случайной выборкой, для сбора данных из конкретной выборки, чтобы потенциально прийти к точному выводу. Если мы используем первый вопрос, указанный выше, данные могут выглядеть так:
| Имя | Статус | Образование | |
| 1 | Мелисса | В разводе | кандидат наук или выше |
| 2 | Кейси | Женатый | Степень бакалавра |
| 3 | Анджела | Женатый | GED |
| 4 | Алисса | Овдовела | Степень бакалавра |
| 5 | Дженна | Никогда не был женат | GED |
Эти таблицы непредвиденных обстоятельств используются в качестве отправной точки для организации данных, собранных с помощью простой случайной выборки.
Преимущества логического анализа
Использование дедуктивного анализа имеет много преимуществ, в основном то, что он обеспечивает избыток подробной информации — гораздо больше, чем после проведения теста описательного анализа.
Эта информация дает исследователям и аналитикам всестороннее представление о взаимосвязях между двумя переменными. Он также может демонстрировать осведомленность о причинах и следствиях и прогнозах относительно тенденций и закономерностей во всех отраслях.
Кроме того, поскольку он так широко используется в деловом мире, а также в академических кругах, это общепризнанный метод статистического анализа.
Ограничения логического анализа
Когда дело доходит до выводной статистики, есть два основных ограничения.
Первое ограничение связано с тем фактом, что, поскольку анализируемые данные получены от населения, которое не было полностью измерено, аналитики данных никогда не могут быть на 100% уверены в правильности вычисляемой статистики. Поскольку выводной анализ основан на процессе использования значений, измеренных в выборке, для вывода значений, которые будут измерены из общей совокупности, всегда будет некоторый уровень неопределенности в отношении результатов.
Второе ограничение заключается в том, что некоторые логические тесты требуют от аналитика или исследователя сделать обоснованное предположение, основанное на теориях для проведения тестов. Подобно первому ограничению, эти догадки будут иметь неопределенность, что также будет иметь некоторые последствия для надежности результатов некоторых статистических тестов.
Не делайте поспешных выводов
Прежде чем вы сделаете потенциально неточный вывод относительно данных, убедитесь, что вы воспользовались информацией, которая ожидает вас в тесте логического анализа.
Независимо от типа вывода, к которому вы хотите прийти, или гипотезы, с которой вы начинаете, вы можете быть удивлены результатами, которые может дать тест логического анализа.
Ищете программное обеспечение для статистического анализа, чтобы лучше интерпретировать все ваши наборы данных? Или, может быть, инструмент, который сделает даже самый сложный статистический анализ простым и убедительным? Ознакомьтесь с нашим списком непредвзятых отзывов о G2!
