تعال إلى الاستنتاج الصحيح مع التحليل الاستنتاجي
نشرت: 2020-03-23نحن جميعًا مذنبون في القفز إلى الاستنتاجات من وقت لآخر.
سواء كنت تقنع نفسك بأن لا أحد سيشتري تذكرة للمؤتمر الذي عملت بجد لتخطط له أو أن الوصول إلى المطار قبل ساعتين ببساطة ليس وقتًا كافيًا ، لقد فعلنا جميعًا ذلك.
خارج حياتنا اليومية ، من السهل القفز إلى استنتاجات غير دقيقة في العمل ، بغض النظر عن الصناعة. عندما نفعل هذا ، فإننا في الأساس نعمم ، ولكن ماذا لو كان بإمكانك جعل هذه التعميمات أكثر دقة؟ من الممكن عند تشغيل اختبارات التحليل الاستنتاجي.
ما هو التحليل الاستنتاجي؟
يستخدم التحليل الاستنتاجي لرسم وقياس مصداقية الاستنتاجات حول السكان والتي تستند إلى المعلومات التي تم جمعها من عينة من السكان. نظرًا لأن التحليل الاستدلالي لا يأخذ عينة من كل فرد في المجتمع ، فستحتوي النتائج دائمًا على مستوى معين من عدم اليقين.
عند الغوص في التحليل الإحصائي ، غالبًا ما يكون حجم السكان الذي نتطلع إلى تحليله كبيرًا جدًا ، مما يجعل من المستحيل دراسة الجميع. في هذه الحالات ، يتم جمع البيانات باستخدام عينات عشوائية من الأفراد ضمن مجموعة سكانية معينة. بعد ذلك ، يتم استخدام التحليل الاستنتاجي على البيانات للوصول إلى استنتاجات حول إجمالي عدد السكان.
نظرًا لأنه غالبًا ما يكون من المستحيل قياس مجموعة كاملة من الأشخاص ، يعتمد التحليل الاستنتاجي على جمع البيانات من عينة من الأفراد داخل المجتمع. بشكل أساسي ، يتم استخدام التحليل الاستنتاجي لمحاولة الاستدلال من عينة البيانات على ما قد يعتقده السكان أو يظهرونه.
هناك طريقتان رئيسيتان للقيام بذلك:
- تقدير المعلمات: أخذ إحصاء من عينة بيانات (مثل متوسط العينة) واستخدامه لاستنتاج شيء عن المجتمع (متوسط المحتوى).
- اختبارات الفرضيات: استخدام عينات البيانات للإجابة على أسئلة بحثية محددة.
في تقدير المعلمات ، تُستخدم العينة لتقدير قيمة تصف المجتمع بأكمله ، بالإضافة إلى فاصل الثقة. ثم يتم إنشاء التقدير.
في اختبار الفرضيات ، تُستخدم البيانات لتحديد ما إذا كانت قوية بما يكفي لدعم أو رفض الافتراض.
التحليل الوصفي مقابل التحليل الاستنتاجي
النوعان الرئيسيان من التحليل الإحصائي الذي يستخدمه الناس غالبًا هما التحليل الوصفي والتحليل الاستنتاجي. لهذا السبب ، ليس من غير المألوف أن يتم الخلط بين الاثنين لبعضهما البعض ، على الرغم من أنهما يوفران لمحللي البيانات رؤى مختلفة حول البيانات التي يتم جمعها.
بينما لا يمكن للمرء عرض الصورة بأكملها ، عند استخدامها معًا ، فإنها توفر أداة قوية لتصور البيانات وتحليلات التنبؤ ، لأنها تعتمد على نفس مجموعة البيانات.
يعطي التحليل الإحصائي الوصفي معلومات تصف البيانات بطريقة ما. يتم ذلك أحيانًا باستخدام المخططات والرسوم البيانية المصممة باستخدام برنامج تصور البيانات لشرح ما تقدمه البيانات. لا يتم استخدام طريقة التحليل الإحصائي هذه لاستخلاص النتائج ، فقط لتلخيص المعلومات.
التحليل الإحصائي الاستنتاجي هو الطريقة التي سيتم استخدامها لاستخلاص النتائج. يسمح للمستخدمين باستنتاج أو استنتاج الاتجاهات حول عدد أكبر من السكان بناءً على العينات التي يتم تحليلها. في الأساس ، يأخذ البيانات من عينة ثم يتوصل إلى استنتاجات حول عدد أكبر من السكان أو المجموعة.
غالبًا ما يستخدم هذا النوع من التحليل الإحصائي لدراسة العلاقة بين المتغيرات داخل العينة ، مما يسمح باستنتاجات وتعميمات تمثل المجتمع بدقة. وعلى عكس التحليل الوصفي ، يمكن للشركات اختبار فرضية والتوصل إلى استنتاجات مختلفة من هذه البيانات.

دعونا نفكر في الأمر بهذه الطريقة. أنت في لعبة بيسبول واسأل عينة من 100 معجب إذا كانوا يحبون النقانق. يمكنك عمل رسم بياني شريطي للإجابات بنعم أو لا ، والذي سيكون تحليلًا وصفيًا. أو يمكنك استخدام بحثك لاستنتاج أن 93٪ من السكان (جميع مشجعي البيسبول في جميع ملاعب البيسبول) يحبون الهوت دوغ ، وهو ما سيكون تحليلًا استنتاجيًا.
أنواع اختبارات التحليل الاستنتاجي
هناك أنواع عديدة من اختبارات التحليل الاستنتاجي الموجودة في مجال الإحصاء. أي واحد تختار استخدامه سيعتمد على حجم عينتك ، والفرضية التي تحاول حلها ، وحجم المجتمع الذي يتم اختباره.
تحليل الانحدار الخطي
يستخدم تحليل الانحدار الخطي لفهم العلاقة بين متغيرين (X و Y) في مجموعة بيانات كطريقة لتقدير المتغير غير المعروف لعمل توقعات مستقبلية حول الأحداث والأهداف.
الهدف الرئيسي لتحليل الانحدار هو تقدير قيم المتغير العشوائي (Z) بناءً على قيم المتغيرات المعروفة (أو الثابتة) (X و Y). يتم تمثيل هذا عادةً بواسطة مخطط مبعثر ، مثل المخطط أدناه.
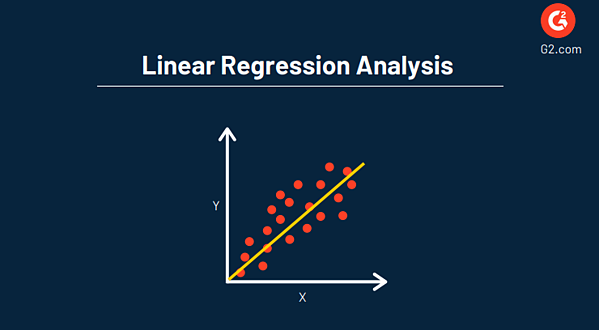
تتمثل إحدى الميزات الرئيسية لاستخدام الانحدار في تحليلك في أنه يوفر نظرة مفصلة على البيانات ويتضمن معادلة يمكن استخدامها للتحليلات التنبؤية وتحسين البيانات في المستقبل.
صيغة تحليل الانحدار هي:
ص = أ + ب (س)
A → يشير إلى تقاطع y ، قيمة y عندما x = 0
B → يشير إلى المنحدر ، أو الارتفاع فوق الجري
تحليل الارتباط
اختبار تحليل استنتاجي آخر هو تحليل الارتباط ، والذي يستخدم لفهم مدى اعتماد متغيرين على بعضهما البعض. يختبر هذا التحليل أساسًا قوة العلاقة بين متغيرين ، وما إذا كان ارتباطهما قويًا أم ضعيفًا.
يمكن أن يكون الارتباط بين متغيرين سالبًا أو موجبًا ، اعتمادًا على المتغيرات. تعتبر المتغيرات "غير مرتبطة" عندما لا يؤثر التغيير في أحدهما على الآخر.
مثال على ذلك سيكون السعر والطلب. وذلك لأن الزيادة في الطلب تؤدي إلى زيادة مقابلة في السعر. سوف يرتفع السعر لأن المزيد من المستهلكين يريدون شيئًا ما وهم على استعداد لدفع المزيد مقابل ذلك.
بشكل عام ، الهدف من تحليل الارتباط هو العثور على القيمة العددية التي توضح العلاقة بين المتغيرين وكيفية تحركهما معًا. مثل الانحدار ، يتم ذلك عادةً عن طريق استخدام برنامج تصور البيانات لإنشاء رسم بياني.
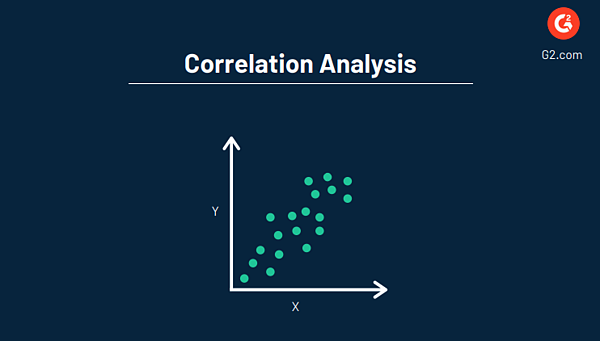
ذات صلة: تعرف على المزيد حول مداخل وعموميات الارتباطات مقابل الانحدار ، بما في ذلك الاختلافات والطريقة التي يجب أن يستخدمها عملك.
تحليل التباين
يتم استخدام الطريقة الإحصائية لتحليل التباين (ANOVA) لاختبار وتحليل الفروق بين وسيلتين أو أكثر من مجموعة البيانات. يتم ذلك عن طريق فحص مقدار التباين بين العينات.
بعبارات أبسط ، توفر ANOVA اختبارًا إحصائيًا لما إذا كانت وسيلتان أو أكثر من الوسائل السكانية متساوية ، بالإضافة إلى تعميم اختبار t بين وسيلتين.
تعرف على المزيد: يستخدم اختبار t لإظهار مدى أهمية الاختلافات بين مجموعتين. بشكل أساسي ، يسمح بفهم ما إذا كانت الاختلافات (المقاسة بالوسائل / المتوسطات) يمكن أن تحدث بالصدفة.

ستسمح هذه الطريقة باختبار المجموعات لمعرفة ما إذا كان هناك فرق بينها. على سبيل المثال ، يمكنك اختبار الطلاب في مدرستين ثانويتين مختلفتين يقومون بإجراء نفس الاختبار لمعرفة ما إذا كانت إحدى المدارس الثانوية أعلى من الأخرى.
يمكن أيضًا تقسيم ANOVA إلى نوعين:
- أحادي الاتجاه: متغير مستقل واحد فقط بمستويين. مثال على ذلك هو نوع من زبدة الفول السوداني.
- ثنائي الاتجاه: متغيران مستقلان يمكن أن يكون لهما مستويات متعددة. مثال على ذلك هو نوع من زبدة الفول السوداني والسعرات الحرارية.
المستوى هو ببساطة المجموعات المختلفة داخل المتغير. لذلك ، باستخدام نفس المثال أعلاه ، قد تكون مستويات العلامات التجارية لزبدة الفول السوداني هي Jif أو Skippy أو Peter Pan. يمكن أن تكون مستويات السعرات الحرارية ناعمة أو كريمية أو عضوية.
تحليل التغاير
تحليل التغاير (ANCOVA) هو مزيج فريد من تحليل التباين (ANOVA) والانحدار. يمكن أن تظهر ANCOVA ما هي المعلومات الإضافية المتاحة عند النظر في متغير أو عامل واحد مستقل في وقت واحد ، دون التأثير على الآخرين.
غالبًا ما يستخدم:
- لتمديد الانحدار المتعدد كطريقة لمقارنة خطوط الانحدار المتعددة
- للتحكم في المتغيرات المشتركة (المتغيرات الأخرى) التي ليست هي المحور الرئيسي لدراستك
- لتمديد تحليل التباين
- لدراسة مجموعات من المتغيرات الأخرى ذات الأهمية
- للتحكم في العوامل التي لا يمكن تحديدها بشكل عشوائي ولكن يمكن قياسها
يمكن أيضًا استخدام ANCOVA للاختبار المسبق أو البعدي لتحليل عندما يؤثر الانحدار إلى المتوسط على قياس الاختبار اللاحق للإحصاء.
على سبيل المثال ، لنفترض أن عملك ينتج أدوية جديدة للجمهور تعمل على خفض ضغط الدم. يمكنك إجراء دراسة تراقب أربع مجموعات علاجية ومجموعة مراقبة واحدة.
إذا كنت تستخدم ANOVA ، فستتمكن من معرفة ما إذا كان العلاج يؤدي في الواقع إلى خفض ضغط الدم. عندما تدمج ANCOVA ، يمكنك التحكم في العوامل الأخرى التي قد تؤثر على النتيجة ، مثل الحياة الأسرية أو المهنة أو استخدام العقاقير التي تستلزم وصفة طبية.
فاصل الثقة
فاصل الثقة هو أداة تُستخدم في التحليل الاستدلالي الذي يقدر معلمة ، وعادة ما تكون المتوسط ، لمحتوى بأكمله. بشكل أساسي ، هو مقدار عدم اليقين الموجود في أي إحصائية معينة ويتم استخدامه عادةً بهامش خطأ.
يتم التعبير عن فاصل الثقة برقم يعكس مدى تأكدك من أن نتائج الاستطلاع أو الاستطلاع هي ما تتوقعه إذا كان من الممكن إجراء مسح للسكان بالكامل.
على سبيل المثال ، إذا كانت نتائج الاستطلاع أو الاستطلاع تحتوي على فاصل ثقة بنسبة 98٪ ، فإن هذا يحدد نطاق القيم التي يمكن أن تكون متأكدًا بنسبة 98٪ أنها تحتوي على متوسط المحتوى. للوصول إلى هذا الاستنتاج ، نحتاج إلى ثلاث معلومات:
- مستوى الثقة : يصف عدم اليقين المرتبط بطريقة أخذ العينات
- الإحصاء: البيانات التي تم جمعها من المسح أو الاستطلاع
- هامش الخطأ : كم عدد النقاط المئوية التي ستختلف فيها نتائجك عن القيمة الحقيقية للسكان
اختبار Chi-Square
يتم استخدام اختبار مربع كاي ، والمعروف باسم اختبار x2 ، لتحديد الفرق بين المجموعات عندما تكون جميع المتغيرات اسمية (تُعرف أيضًا باسم متغير له قيم ليس لها قيمة عددية) ، مثل الجنس ، فجوة الرواتب والانتماء السياسي وما إلى ذلك.
تُستخدم هذه الاختبارات عادةً مع جداول طوارئ محددة تجمع الملاحظات بناءً على الخصائص المشتركة.
قد تكون الأسئلة التي يمكن أن يجيب عليها اختبار تشي سكوير:
- هل يرتبط مستوى التعليم والحالة الاجتماعية لجميع الأشخاص في الولايات المتحدة؟
- هل هناك علاقة بين نية الناخب وعضوية الحزب السياسي؟
- هل يؤثر الجنس في أي عطلة يفضلها الناس؟
عادة ، يتم إجراء هذه الاختبارات باستخدام طريقة التحليل الإحصائي التي تسمى أخذ العينات العشوائية البسيطة لجمع البيانات من عينة محددة للوصول إلى نتيجة دقيقة. إذا استخدمنا السؤال الأول المذكور أعلاه ، فقد تبدو البيانات كما يلي:
| اسم | حالة | تعليم | |
| 1 | ميليسا | مُطلّق | دكتوراه أو أعلى |
| 2 | كيسي | متزوج | درجة باكلريوس |
| 3 | أنجيلا | متزوج | جد |
| 4 | أليسا | الأرامل | درجة باكلريوس |
| 5 | جينا | لم يتزوج قط | جد |
تُستخدم جداول الطوارئ هذه كنقطة انطلاق لتنظيم البيانات التي تم جمعها من خلال أخذ عينات عشوائية بسيطة.
مزايا التحليل الاستنتاجي
هناك العديد من المزايا لاستخدام التحليل الاستدلالي ، خاصة أنه يوفر فائضًا من المعلومات التفصيلية - أكثر بكثير مما كنت ستحصل عليه بعد إجراء اختبار التحليل الوصفي.
توفر هذه المعلومات للباحثين والمحللين رؤى شاملة للعلاقات بين متغيرين. ويمكنه أيضًا إظهار الوعي تجاه السبب والنتيجة والتنبؤات المتعلقة بالاتجاهات والأنماط في جميع الصناعات.
بالإضافة إلى ذلك ، نظرًا لاستخدامها على نطاق واسع في عالم الأعمال والأوساط الأكاديمية ، فهي طريقة مقبولة عالميًا للتحليل الإحصائي.
حدود التحليل الاستنتاجي
عندما يتعلق الأمر بالإحصاءات الاستنتاجية ، هناك نوعان من القيود الرئيسية.
يأتي القيد الأول من حقيقة أنه نظرًا لأن البيانات التي يتم تحليلها هي من مجموعة لم يتم قياسها بالكامل ، فلا يمكن لمحللي البيانات أن يكونوا متأكدين بنسبة 100 ٪ من صحة الإحصائيات التي يتم حسابها. نظرًا لأن التحليل الاستنتاجي يعتمد على عملية استخدام القيم المقاسة في عينة لاستنتاج القيم التي سيتم قياسها من إجمالي عدد السكان ، فسيكون هناك دائمًا مستوى معين من عدم اليقين فيما يتعلق بالنتائج.
القيد الثاني هو أن بعض الاختبارات الاستدلالية تتطلب من المحلل أو الباحث إجراء تخمين مستنير بناءً على النظريات لإجراء الاختبارات. على غرار القيد الأول ، سيكون هناك عدم يقين يحيط بهذه التخمينات ، مما يعني أيضًا بعض التداعيات على موثوقية نتائج بعض الاختبارات الإحصائية.
لا تقفز إلى الاستنتاجات
قبل أن تقفز إلى نتيجة يحتمل أن تكون غير دقيقة فيما يتعلق بالبيانات ، تأكد من الاستفادة من المعلومات التي تنتظر في اختبار التحليل الاستنتاجي.
بغض النظر عن نوع الاستنتاج الذي تتطلع إلى التوصل إليه ، أو الفرضية التي تبدأ بها ، فقد تفاجأ بالنتائج التي يمكن أن يحققها اختبار التحليل الاستنتاجي.
هل تبحث عن برنامج تحليل إحصائي لتفسير جميع مجموعات البيانات الخاصة بك بشكل أفضل؟ أو ربما أداة تجعل حتى أكثر التحليل الإحصائي تعقيدًا بسيطًا وقاطعًا؟ تحقق من قائمة المراجعات غير المتحيزة على G2!
