วิธีตรวจสอบว่าตัวเลขเป็นจำนวนเฉพาะใน Python หรือไม่
เผยแพร่แล้ว: 2022-05-02บทช่วยสอนนี้จะสอนวิธีเขียนโปรแกรม Python เพื่อตรวจสอบว่า ตัวเลขเป็นจำนวนเฉพาะ หรือไม่
หากคุณเคยทำแบบทดสอบการเขียนโค้ด คุณจะเจอคำถามทางคณิตศาสตร์เกี่ยวกับการทดสอบความเป็นอันดับหนึ่งหรือเพื่อตรวจสอบว่าตัวเลขเป็นจำนวนเฉพาะหรือไม่ และในอีกไม่กี่นาทีข้างหน้า คุณจะได้เรียนรู้วิธีแก้ไขปัญหาที่เหมาะสมที่สุดสำหรับคำถามนี้
ในบทช่วยสอนนี้ คุณจะ:
- ทบทวนพื้นฐานของจำนวนเฉพาะ
- เขียนโค้ด Python เพื่อตรวจสอบว่าตัวเลขเป็นจำนวนเฉพาะหรือไม่ และ
- เพิ่มประสิทธิภาพเพิ่มเติมเพื่อรับอัลกอริธึมรันไทม์ O(√n)
สำหรับสิ่งนี้และอื่น ๆ มาเริ่มกันเลย
ไพรม์นัมเบอร์คืออะไร?
เริ่มต้นด้วยการทบทวนพื้นฐานของจำนวนเฉพาะ
ในทฤษฎีจำนวน จำนวนธรรมชาติ n กล่าวว่าเป็นจำนวนเฉพาะถ้ามันมี ตัวประกอบ สองตัวพอดี กันคือ 1 และตัวของมันเอง ( n ) จำจากคณิตศาสตร์ของโรงเรียนของคุณ: จำนวน i ถูกกล่าวว่าเป็นตัวประกอบของจำนวน n ถ้า ฉัน หาร n เท่ากัน
ตารางต่อไปนี้แสดงรายการตัวเลขสองสามตัว ตัวประกอบทั้งหมด และว่าเป็นจำนวนเฉพาะหรือไม่
| น | ปัจจัย | เป็นไพรม์? |
| 1 | 1 | ไม่ |
| 2 | 1,2 | ใช่ |
| 3 | 1, 3 | ใช่ |
| 4 | 1, 2, 4 ปี | ไม่ |
| 7 | 1,7 | ใช่ |
| 15 | 1, 3, 5, 15 ปี | ไม่ |
จากตารางข้างต้น เราสามารถเขียนสิ่งต่อไปนี้:
- 2 เป็นจำนวนเฉพาะที่น้อยที่สุด
- 1 เป็นตัวประกอบของทุกจำนวน
- ทุกจำนวน
nเป็นตัวประกอบของตัวมันเอง
ดังนั้น 1 และ n จึงเป็นตัวประกอบเล็กน้อยสำหรับจำนวน n ใดๆ และจำนวนเฉพาะไม่ควรมีตัวประกอบอื่นใดนอกจากสองตัวนี้
ซึ่งหมายความว่าเมื่อคุณเปลี่ยนจาก 2 เป็น n – 1 คุณ ไม่ ควรจะหาตัวประกอบที่ไม่สำคัญที่หาร n โดยไม่มีเศษเหลือ
O(n) อัลกอริธึมเพื่อตรวจสอบว่าตัวเลขเป็นจำนวนเฉพาะใน Python หรือไม่
ในส่วนนี้ ให้เรากำหนดวิธีการข้างต้นให้เป็นฟังก์ชัน Python อย่างเป็นทางการ
คุณสามารถวนซ้ำตัวเลขทั้งหมดตั้งแต่ 2 ถึง n – 1 โดยใช้วัตถุ range() ใน Python
ใน Python
range(start, stop, step)จะคืนค่าวัตถุ range จากนั้น คุณสามารถวนซ้ำวัตถุ range เพื่อรับลำดับตั้งแต่startจนถึงstop -1ในขั้นตอนของstep
เนื่องจากเราต้องการเซตของจำนวนเต็มตั้งแต่ 2 ถึง n-1 เราจึงสามารถระบุ range(2, n) และใช้ร่วมกับ for loop
นี่คือสิ่งที่เราต้องการจะทำ:
- หากคุณพบจำนวนที่หาร n เท่ากันโดยไม่มีเศษเหลือ คุณสามารถสรุปได้ทันทีว่าจำนวนนั้นไม่เป็นจำนวนเฉพาะ
- หากคุณวนรอบตัวเลขทั้งหมดตั้งแต่ 2 ไปจนถึง n – 1 โดยไม่พบตัวเลขที่หาร n เท่ากัน แสดงว่าจำนวนนั้นเป็นจำนวนเฉพาะ
ฟังก์ชัน Python สำหรับตรวจสอบ Prime Number
เมื่อใช้ข้างต้น เราสามารถไปข้างหน้าและกำหนดฟังก์ชัน is_prime() ได้ดังนี้
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return Trueตอนนี้เรามาแยกคำจำกัดความของฟังก์ชันด้านบนกัน
- ฟังก์ชันข้างต้น
is_prime()รับจำนวนเต็มบวก n เป็นอาร์กิวเมนต์ - หากคุณพบตัวประกอบในช่วงที่ระบุ (2, n-1) ฟังก์ชันจะคืนค่า
Falseเนื่องจากตัวเลขไม่ใช่จำนวนเฉพาะ - และจะส่งกลับ
Trueหากคุณสำรวจลูปทั้งหมดโดยไม่พบปัจจัย
ต่อไป ให้เรียกใช้ฟังก์ชันที่มีอาร์กิวเมนต์และตรวจสอบว่าผลลัพธ์ถูกต้องหรือไม่
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True ในผลลัพธ์ด้านบน คุณเห็นว่า 2 และ 11 เป็นจำนวนเฉพาะ (ฟังก์ชันคืนค่า True ) และ 8 และ 9 ไม่ใช่จำนวนเฉพาะ (ฟังก์ชันจะคืนค่า False )
วิธีเพิ่มประสิทธิภาพฟังก์ชัน Python is_prime()
เราสามารถเพิ่มประสิทธิภาพเล็กๆ น้อยๆ ได้ที่นี่ สังเกตรายการปัจจัยในตารางด้านล่าง
| ตัวเลข | ปัจจัย |
| 6 | 1, 2, 3 , 6 เดือน |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
เราเห็นแล้วว่าตัวประกอบของ n ตัวเดียวที่มากกว่า n/2 คือตัว n ตัวมันเอง
นี่หมายความว่าคุณไม่จำเป็นต้องวนซ้ำจนถึง n – 1 คุณสามารถรันลูปได้มากถึง n/2 เท่านั้น
หากคุณไม่พบปัจจัยที่ไม่สำคัญจนถึง n/2 คุณจะไม่พบปัจจัยที่เกิน n/2 เช่นกัน
ตอนนี้ มาแก้ไขฟังก์ชัน is_prime() เพื่อตรวจสอบปัจจัยในช่วง (2, n/2)
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return Trueไปข้างหน้าและตรวจสอบผลลัพธ์ผ่านการเรียกใช้ฟังก์ชันสองสามรายการ
is_prime(9) # False is_prime(11) # Trueแม้ว่าดูเหมือนว่าเราได้ปรับให้เหมาะสมแล้ว แต่อัลกอริธึมนี้ไม่ได้มีประสิทธิภาพมากกว่าอัลกอริธึมก่อนหน้าในแง่ของความซับซ้อนรันไทม์ อันที่จริง ทั้งคู่มีความซับซ้อนรันไทม์ O(n) : เป็นสัดส่วนกับค่าของ n หรือเชิงเส้นใน n
เราสามารถทำได้ดีกว่านี้หรือไม่? ใช่เราทำได้!
️ ไปที่ส่วนถัดไปเพื่อกำหนดวิธีปรับปรุงความซับซ้อนของเวลาสำหรับการทดสอบจำนวนเฉพาะ
O(√n) อัลกอริทึมเพื่อตรวจสอบหมายเลขเฉพาะใน Python
มันเกิดขึ้นที่ตัวประกอบของตัวเลขเกิดขึ้นเป็นคู่
ถ้า a เป็นตัวประกอบของจำนวน n ก็จะมีตัวประกอบ b เช่นกัน ซึ่ง axb = n หรือง่ายๆ ก็คือ ab = n
ลองตรวจสอบสิ่งนี้ด้วยตัวอย่าง
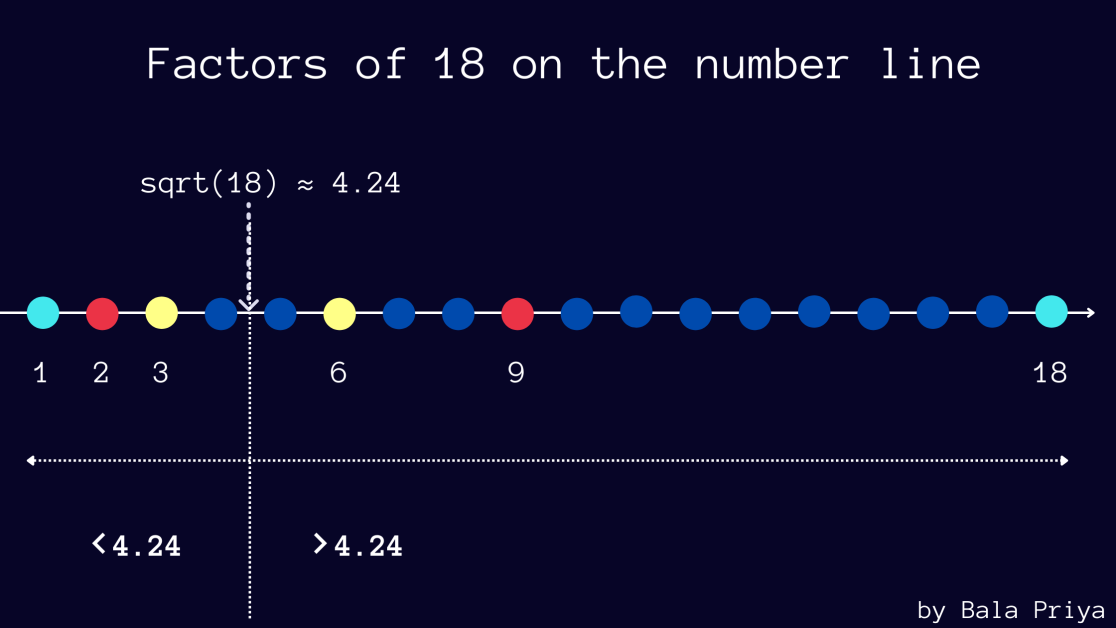
ตารางด้านล่างแสดงปัจจัยของจำนวน 18 ที่เกิดขึ้นเป็นคู่ คุณสามารถยืนยันหมายเลขเดียวกันได้อีกสองสามหมายเลขหากต้องการ
นอกจากนี้ โปรดทราบว่า √18 มีค่าประมาณ 4.24
และในปัจจัยที่เกิดขึ้นเป็นคู่ (a, b) คุณจะเห็นได้ว่าถ้า a น้อยกว่า 4.24 แล้ว b จะมากกว่า 4.24—ในตัวอย่างนี้ (2, 18) และ (3, 6)
| เอ | ข |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
รูปด้านล่างแสดงตัวประกอบของ 18 ที่พล็อตบนเส้นจำนวน
หากตัวเลข n เป็นกำลังสองสมบูรณ์ คุณจะมี a = b = √n เป็นปัจจัยหนึ่ง
️ ดูตัวประกอบของ 36 ในตารางด้านล่าง เนื่องจาก 36 เป็นกำลังสองสมบูรณ์ a = b = 6 จึงเป็นหนึ่งในปัจจัย สำหรับคู่ปัจจัยอื่นๆ ทั้งหมด (a, b) a < 6 และ b > 6 จะคงอยู่
| เอ | ข |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
สรุปเรามีดังต่อไปนี้:
- ทุกตัวเลข n สามารถเขียนเป็น n = axb
- ถ้า n เป็นกำลังสองสมบูรณ์ แล้ว a = b = √n .
- และถ้า a < b แล้ว a < √n และ b > √n .
- มิฉะนั้น ถ้า a > b แล้ว a > √n และ b < √n
ดังนั้นแทนที่จะวนซ้ำจำนวนเต็มทั้งหมดสูงถึง n/2 คุณอาจเลือกที่จะรันสูงถึง √n และนี่มีประสิทธิภาพมากกว่าวิธีการก่อนหน้านี้ของเรามาก
วิธีการแก้ไข is_prime() เป็น O(√n) อัลกอริธึม
มาเพิ่มประสิทธิภาพการทำงานของฟังก์ชันเพื่อตรวจสอบจำนวนเฉพาะใน Python กัน
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return Trueตอนนี้ มาแยกคำนิยามฟังก์ชันด้านบนกัน:
- ในการคำนวณรากที่สองของตัวเลข ให้นำเข้าโมดูลคณิตศาสตร์ในตัวของ Python และใช้
math.sqrt() - เนื่องจาก n อาจไม่ใช่กำลังสองสมบูรณ์ เราจึงต้องใส่มันเป็นจำนวนเต็ม ใช้
int(var)เพื่อส่งvarเป็นint - เพื่อให้แน่ใจว่าเรากำลังตรวจสอบถึง √n จริงๆ เราจึงเพิ่มเครื่องหมายบวกหนึ่งเนื่องจากฟังก์ชัน
range()จะไม่รวมจุดสิ้นสุดของช่วงโดยค่าเริ่มต้น
เซลล์รหัสด้านล่างตรวจสอบว่าฟังก์ชันของเรา is_prime() ทำงานอย่างถูกต้อง
is_prime(8) # False is_prime(15) # False is_prime(23) # Trueในส่วนถัดไป ให้เราสร้างแผนภาพง่ายๆ เพื่อทำความเข้าใจ O(n) และ O(√n) ด้วยสายตา
เปรียบเทียบ O(n) และ O(√n) ด้วยสายตา
️ เรียกใช้ข้อมูลโค้ดต่อไปนี้ในสภาพแวดล้อมสมุดบันทึก Jupyter ที่คุณเลือก
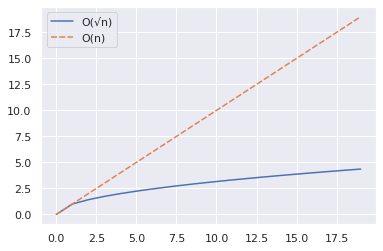
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)ตัวอย่างด้านบนแสดงวิธีที่คุณสามารถพล็อตเส้นโค้งสำหรับ n และ √n สำหรับช่วงของค่าต่างๆ
- เราใช้ฟังก์ชัน NumPy arange() เพื่อสร้างอาร์เรย์ของตัวเลข
- จากนั้น เรารวบรวมค่าของ n และ √n สูงสุด แต่ไม่รวม 20 ลงใน DataFrame แพนด้า
- ต่อไป เราวางแผนโดยใช้ฟังก์ชัน lineplot() ของ seaborn
จากแผนภาพด้านล่าง เราจะเห็นว่า √n น้อยกว่า n อย่างเห็นได้ชัด
ให้เราเพิ่มช่วงให้สูงถึง 2,000 และทำซ้ำขั้นตอนเดียวกันกับข้างต้น
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 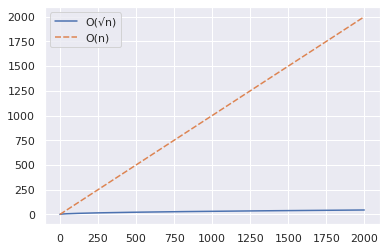
จากพล็อตด้านบนนี้ คุณสามารถอนุมานได้ว่าอัลกอริทึม O(√n) นั้นเร็วขึ้นอย่างมากเมื่อคุณทำการทดสอบว่าตัวเลขจำนวนมากเป็นจำนวนเฉพาะหรือไม่
นี่คือตัวอย่างสั้นๆ: 2377 เป็นจำนวนเฉพาะ—ยืนยันสิ่งนี้!
แม้ว่าวิธี O(n) จะใช้ลำดับ 2,000 ขั้นตอน แต่อัลกอริธึม O(√n) สามารถช่วยให้ได้คำตอบในเวลาเพียง 49 ขั้นตอน
บทสรุป
และก็ถึงเวลาสำหรับการสรุปอย่างรวดเร็ว
- ในการตรวจสอบว่าตัวเลขเป็นจำนวนเฉพาะหรือไม่ วิธีไร้เดียงสาคือการวนซ้ำตัวเลขทั้งหมดในช่วง (2, n-1) หากคุณไม่พบตัวประกอบที่หาร n แล้ว n เป็นจำนวนเฉพาะ
- เนื่องจากตัวประกอบเพียงตัวเดียวของ n ที่มากกว่า n/2 คือตัว n ตัวมันเอง คุณอาจเลือกที่จะวิ่งได้ถึง n/2 เท่านั้น
- ทั้งสองวิธีข้างต้นมีความซับซ้อนของเวลาเป็น O(n)
- เนื่องจากตัวประกอบของตัวเลขเกิดขึ้นเป็นคู่ คุณสามารถรันได้มากถึง √n เท่านั้น อัลกอริทึมนี้เร็วกว่า O(n) มาก และค่าเกนนั้นสามารถประเมินได้เมื่อตรวจสอบว่าจำนวนมากเป็นจำนวนเฉพาะหรือไม่
ฉันหวังว่าคุณจะเข้าใจวิธีการตรวจสอบว่าตัวเลขเป็นจำนวนเฉพาะใน Python ได้อย่างไร ในขั้นตอนต่อไป คุณสามารถดูบทช่วยสอนของเราเกี่ยวกับโปรแกรม Python เกี่ยวกับการดำเนินการสตริง ซึ่งคุณจะได้เรียนรู้วิธีตรวจสอบว่าสตริงคือพาลินโดรม แอนนาแกรม และอื่นๆ
แล้วพบกันใหม่กับการกวดวิชาอื่น ถึงเวลานั้น ขอให้สนุกกับการเขียนโค้ด!

