Python'da Bir Sayının Asal Olup Olmadığı Nasıl Kontrol Edilir
Yayınlanan: 2022-05-02Bu eğitim size bir sayının asal olup olmadığını kontrol etmek için bir Python programının nasıl yazılacağını öğretecektir.
Daha önce kodlama testleri yaptıysanız, asallık veya bir sayının asal olup olmadığını kontrol etme testinde matematik sorusuna rastlamışsınızdır. Ve sonraki birkaç dakika içinde, bu soruya en uygun çözümü bulmayı öğreneceksiniz.
Bu eğitimde şunları yapacaksınız:
- asal sayıların temellerini gözden geçirin,
- bir sayının asal olup olmadığını kontrol etmek için Python kodunu yazın ve
- bir O(√n) çalışma zamanı algoritması elde etmek için daha da optimize edin.
Tüm bunlar ve daha fazlası için haydi başlayalım.
Asal Sayı nedir?
Asal sayıların temellerini gözden geçirerek başlayalım.
Sayı teorisinde, n doğal sayısının tam olarak iki çarpanı varsa asal olduğu söylenir: 1 ve sayının kendisi ( n ). Okul matematiğinizden hatırlayın: bir i sayısının, n'yi eşit olarak bölerse , n sayısının bir çarpanı olduğu söylenir.
Aşağıdaki tablo birkaç sayıyı, bunların tüm faktörlerini ve asal olup olmadıklarını listeler.
| n | Faktörler | Başbakan mı? |
| 1 | 1 | Numara |
| 2 | 1, 2 | Evet |
| 3 | 1, 3 | Evet |
| 4 | 1, 2, 4 | Numara |
| 7 | 1, 7 | Evet |
| 15 | 1, 3, 5, 15 | Numara |
Yukarıdaki tablodan aşağıdakileri yazabiliriz:
- 2 en küçük asal sayıdır.
- 1 her sayının çarpanıdır.
- Her
nsayısı kendisinin bir çarpanıdır.
Yani 1 ve n, herhangi bir n sayısı için önemsiz çarpanlardır. Ve bir asal sayının bu ikisinden başka çarpanı olmamalıdır.
Bu, 2'den n – 1'e gittiğinizde, n'yi kalansız bölen önemsiz bir çarpan bulamamanız gerektiği anlamına gelir.
Python'da Bir Sayının Asal Olup Olmadığını Kontrol Eden O(n) Algoritması
Bu bölümde, yukarıdaki yaklaşımı bir Python işlevine resmileştirelim.
Python'da range() nesnesini kullanarak 2'den n - 1'e kadar tüm sayılar arasında döngü yapabilirsiniz.
Python'da
range(start, stop, step)bir aralık nesnesi döndürür. Daha sonra,stepadımlardastartsonastop -1kadar bir dizi elde etmek için aralık nesnesini yineleyebilirsiniz.
2'den n-1'e kadar tamsayılara ihtiyacımız olduğundan, range(2, n) belirtebilir ve bunu for döngüsü ile birlikte kullanabiliriz.
İşte yapmak istediğimiz şey:
- n'yi kalansız bölen bir sayı bulursanız, hemen o sayının asal olmadığı sonucuna varabilirsiniz.
- 2'den n - 1'e kadar tüm sayı aralığında n'yi eşit olarak bölen bir sayı bulmadan dolaştıysanız, sayı asaldır.
Asal Sayıyı Kontrol Eden Python İşlevi
Yukarıdakileri kullanarak devam edip is_prime() fonksiyonunu aşağıdaki gibi tanımlayabiliriz.
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return TrueŞimdi yukarıdaki fonksiyon tanımını ayrıştıralım.
- Yukarıdaki
is_prime()işlevi, argüman olarak pozitif bir n tamsayısını alır. - Belirtilen (2, n-1) aralığında bir faktör bulursanız, sayı asal olmadığı için işlev
Falsedeğerini döndürür. - Ve bir faktör bulmadan tüm döngüyü geçerseniz
Truedeğerini döndürür.
Ardından, argümanlarla işlevi çağıralım ve çıktının doğru olup olmadığını kontrol edelim.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True Yukarıdaki çıktıda, 2 ve 11'in asal olduğunu görüyorsunuz (işlev True değerini döndürür). Ve 8 ve 9 asal değildir (işlev False döndürür).
Python İşlevi Nasıl Optimize Edilir is_prime()
Burada küçük bir optimizasyon yapabiliriz. Aşağıdaki tablodaki faktörlerin listesini inceleyin.
| Sayı | Faktörler |
| 6 | 1, 2, 3 , 6 |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
Pekala, n'nin n/2'den büyük olan tek faktörünün n'nin kendisi olduğunu görebiliriz.
Yani bu, n – 1'e kadar tüm yolu döngüye sokmak zorunda olmadığınız anlamına gelir. Bunun yerine döngüyü yalnızca n/2'ye kadar çalıştırabilirsiniz.
n/2'ye kadar önemsiz olmayan bir faktör bulamazsanız, n/2'nin ötesinde bir faktör de bulamazsınız.
Şimdi (2, n/2) aralığındaki faktörleri kontrol etmek için is_prime() fonksiyonunu değiştirelim.
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return TrueDevam edelim ve çıktıyı birkaç işlev çağrısıyla doğrulayalım.
is_prime(9) # False is_prime(11) # TrueOptimize etmiş gibi görünsek de bu algoritma çalışma zamanı karmaşıklığı açısından bir öncekinden daha verimli değil. Aslında, her ikisi de O(n) çalışma zamanı karmaşıklığına sahiptir: n'nin değeriyle orantılı veya n'de doğrusal.
Daha iyisini yapabilir miyiz? Evet yapabiliriz!
️ Asal sayı testi için zaman karmaşıklığının nasıl iyileştirileceğini belirlemek için sonraki bölüme geçin.
Python'da Asal Sayıyı Kontrol Etmek İçin O(√n) Algoritması
Bir sayının faktörleri çiftler halinde ortaya çıkar.
a , n sayısının bir çarpanıysa, axb = n veya basitçe ab = n olacak şekilde bir b faktörü de vardır.
Bunu bir örnek üzerinden doğrulayalım.
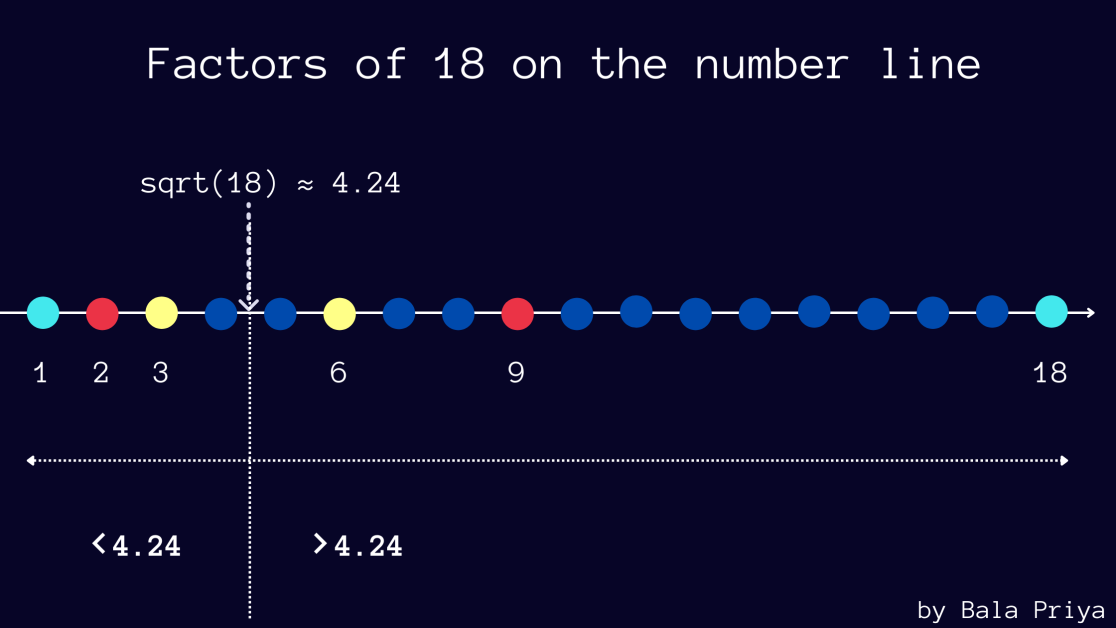
Aşağıdaki tablo çiftler halinde meydana gelen 18 sayısının çarpanlarını göstermektedir. İsterseniz aynısını birkaç numara için daha doğrulayabilirsiniz.
Ayrıca, √18'in yaklaşık 4,24 olduğunu unutmayın.
Ve (a, b) çiftlerinde meydana gelen çarpanlarda, a 4,24'ten küçükse, b'nin 4,24'ten büyük olduğunu görebilirsiniz - bu örnekte (2, 18) ve (3, 6).
| a | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
Aşağıdaki şekil, sayı doğrusunda çizilen 18'in çarpanlarını göstermektedir.
n sayısı bir tam kare ise, çarpanlardan biri olarak a = b = √n olur.
️ Aşağıdaki tabloda 36'nın çarpanlarına bakın. 36 tam kare olduğundan, a = b = 6 çarpanlardan biridir. Diğer tüm faktör çiftleri (a, b) için a < 6 ve b > 6 geçerlidir.
| a | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
Özetle, aşağıdakilere sahibiz:
- Her n sayısı n = axb olarak yazılabilir
- n bir tam kare ise, o zaman a = b = √n .
- Ve eğer a < b , o zaman a < √n ve b > √n .
- Aksi takdirde, eğer a > b ise, o zaman a > √n ve b < √n .
Bu nedenle, n/2'ye kadar tüm tamsayılar arasında döngü yapmak yerine, √n'ye kadar koşmayı seçebilirsiniz. Ve bu, önceki yaklaşımımızdan çok daha verimli.
is_prime()'ı O(√n) Algoritmasına Nasıl Değiştirirsiniz
Python'da asal sayıları kontrol etmek için işlevi optimize etmeye devam edelim.
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return TrueŞimdi yukarıdaki fonksiyon tanımını ayrıştıralım:
- Bir sayının karekökünü hesaplamak için Python'un yerleşik matematik modülünü içe aktaralım ve
math.sqrt()işlevini kullanalım. - n tam bir kare olmayabileceğinden, onu bir tamsayıya çevirmemiz gerekecek. Var'ı bir
intvardönüştürmek içinint(var)kullanın. - Gerçekten √n'ye kadar kontrol ettiğimizden emin olmak için,
range()işlevi varsayılan olarak aralığın bitiş noktasını hariç tuttuğundan artı bir ekleriz.
Aşağıdaki kod hücresi, is_prime() doğru çalıştığını doğrular.
is_prime(8) # False is_prime(15) # False is_prime(23) # TrueBir sonraki bölümde, O(n) ve O(√n)'yi görsel olarak anlamak için birkaç basit grafik oluşturalım.
O(n) ve O(√n)'yi Görsel Olarak Karşılaştırma
️ Aşağıdaki kod parçacığını seçtiğiniz bir Jupyter not defteri ortamında çalıştırın.
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)Yukarıdaki pasaj, bir değer aralığı için n ve √n eğrilerini nasıl çizebileceğinizi gösterir.
- Bir sayı dizisi oluşturmak için NumPy arange() işlevini kullanırız.
- Ardından, n ve √n'nin 20'ye kadar olan değerlerini bir panda DataFrame'de topluyoruz.
- Ardından, seaborn'un lineplot() işlevini kullanarak çizim yapıyoruz.
Aşağıdaki grafikten, √n'nin n'den önemli ölçüde daha küçük olduğunu görüyoruz.
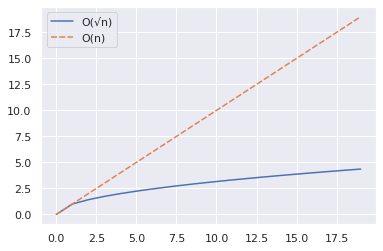
Şimdi aralığı 2000'e çıkaralım ve yukarıdaki adımların aynısını tekrarlayalım.
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 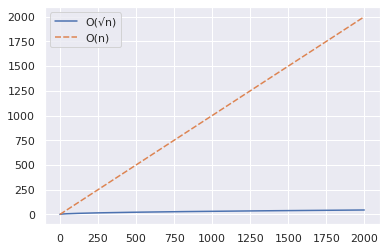
Yukarıdaki çizimden, büyük bir sayının asal olup olmadığını test ederken O(√n) algoritmasının önemli ölçüde daha hızlı olduğunu çıkarabilirsiniz.
İşte hızlı bir örnek: 2377 bir asal sayıdır—bunu doğrulayın!
O(n) yaklaşımı 2000 adım sırasını alırken, O(√n) algoritması cevaba sadece 49 adımda ulaşmaya yardımcı olabilir.
Çözüm
Ve hızlı bir özet zamanı.
- Bir sayının asal olup olmadığını kontrol etmek için, saf yaklaşım (2, n-1) aralığındaki tüm sayılar arasında döngü yapmaktır. n'yi bölen bir çarpan bulamazsanız, n asaldır.
- n/2'den büyük n'nin tek faktörü n'nin kendisi olduğundan, yalnızca n/2'ye kadar çalıştırmayı seçebilirsiniz.
- Yukarıdaki yaklaşımların her ikisi de O(n) zaman karmaşıklığına sahiptir.
- Bir sayının çarpanları çiftler halinde oluştuğundan, yalnızca √n'ye kadar koşabilirsiniz. Bu algoritma O(n)'den çok daha hızlıdır. Ve büyük bir sayının asal olup olmadığını kontrol ederken kazanç kayda değerdir.
Umarım Python'da bir sayının asal olup olmadığını nasıl kontrol edeceğinizi anlamışsınızdır. Bir sonraki adım olarak, dizgelerin palindrom, anagram ve daha fazlası olup olmadığını kontrol etmeyi öğreneceğiniz dizge işlemleriyle ilgili Python programları hakkındaki eğitimimize göz atabilirsiniz.
Bir başka eğitimde görüşmek üzere. O zamana kadar, mutlu kodlamalar!

