Como verificar se um número é primo em Python
Publicados: 2022-05-02Este tutorial ensinará como escrever um programa em Python para verificar se um número é primo ou não.
Se você já fez testes de codificação, já se deparou com a questão matemática no teste de primalidade ou para verificar se um número é primo. E nos próximos minutos, você aprenderá a encontrar a solução ideal para essa questão.
Neste tutorial, você irá:
- reveja o básico dos números primos,
- escrever código Python para verificar se um número é primo e
- otimize-o ainda mais para obter um algoritmo de tempo de execução O(√n).
Por tudo isso e muito mais, vamos começar.
O que é um número primo?
Vamos começar revisando o básico dos números primos.
Na teoria dos números, um número natural n é dito primo se tiver exatamente dois fatores : 1 e o próprio número ( n ). Lembre-se de sua matemática da escola: um número i é considerado um fator do número n , se i dividir n uniformemente.
A tabela a seguir lista alguns números, todos os seus fatores e se eles são primos.
| n | Fatores | é Prime? |
| 1 | 1 | Não |
| 2 | 1, 2 | Sim |
| 3 | 1, 3 | Sim |
| 4 | 1, 2, 4 | Não |
| 7 | 1, 7 | Sim |
| 15 | 1, 3, 5, 15 | Não |
A partir da tabela acima, podemos escrever o seguinte:
- 2 é o menor número primo.
- 1 é um fator de cada número.
- Todo número
né um fator de si mesmo.
Então 1 e n são fatores triviais para qualquer número n. E um número primo não deve ter outros fatores além desses dois.
Isso significa que, quando você for de 2 para n – 1, não poderá encontrar um fator não trivial que divida n sem deixar resto.
O(n) Algoritmo para verificar se um número é primo em Python
Nesta seção, vamos formalizar a abordagem acima em uma função Python.
Você pode percorrer todos os números de 2 a n – 1 usando o objeto range() em Python.
Em Python,
range(start, stop, step)retorna um objeto range. Você pode então iterar sobre o objeto range para obter uma sequência desde ostartaté astop -1em etapas destep.
Como precisamos do conjunto de inteiros de 2 a n-1, podemos especificar range(2, n) e usá-lo em conjunto com for .
Aqui está o que gostaríamos de fazer:
- Se você encontrar um número que divida n uniformemente sem deixar resto, poderá concluir imediatamente que o número não é primo.
- Se você percorreu todo o intervalo de números de 2 até n – 1 sem encontrar um número que divida n uniformemente, então o número é primo.
Função Python para verificar o número primo
Usando o acima, podemos seguir em frente e definir a função is_prime() da seguinte forma.
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return TrueVamos agora analisar a definição de função acima.
- A função acima
is_prime()recebe um inteiro positivo n como argumento. - Se você encontrar um fator no intervalo especificado de (2, n-1), a função retornará
False— pois o número não é primo. - E retorna
Truese você percorrer todo o loop sem encontrar um fator.
Em seguida, vamos chamar a função com argumentos e verificar se a saída está correta.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True Na saída acima, você vê que 2 e 11 são primos (a função retorna True ). E 8 e 9 não são primos (a função retorna False ).
Como otimizar a função Python is_prime()
Podemos fazer uma pequena otimização aqui. Observe a lista de fatores na tabela abaixo.
| Número | Fatores |
| 6 | 1, 2, 3 , 6 |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
Bem, podemos ver que o único fator de n que é maior que n/2 é o próprio n .
Portanto, isso significa que você não precisa fazer um loop até n – 1. Em vez disso, você pode executar o loop apenas até n/2.
Se você não encontrar um fator não trivial até n/2, também não poderá encontrar um além de n/2.
Agora vamos modificar a função is_prime() para verificar os fatores no intervalo (2, n/2)
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return TrueVamos em frente e verificar a saída por meio de algumas chamadas de função.
is_prime(9) # False is_prime(11) # TrueEmbora possa parecer que otimizamos, esse algoritmo não é mais eficiente que o anterior em termos de complexidade de tempo de execução. Na verdade, ambos têm complexidade de tempo de execução O(n) : proporcional ao valor de n ou linear em n.
Podemos fazer melhor? Sim, nós podemos!
️ Vá para a próxima seção para determinar como melhorar a complexidade do tempo para o teste de números primos.
Algoritmo O(√n) para verificar o número primo em Python
Acontece que os fatores de um número ocorrem em pares.
Se a é um fator do número n , então também existe um fator b tal que axb = n , ou simplesmente, ab = n .
Vamos verificar isso através de um exemplo.
A tabela abaixo mostra os fatores do número 18 ocorrendo em pares. Você pode verificar o mesmo para mais alguns números, se quiser.
Observe também que √18 é aproximadamente 4,24.
E nos fatores que ocorrem em pares (a, b) , você pode ver que se a for menor que 4,24, então b é maior que 4,24 — neste exemplo, (2, 18) e (3, 6).
| uma | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
A figura abaixo mostra os fatores de 18 plotados na reta numérica.
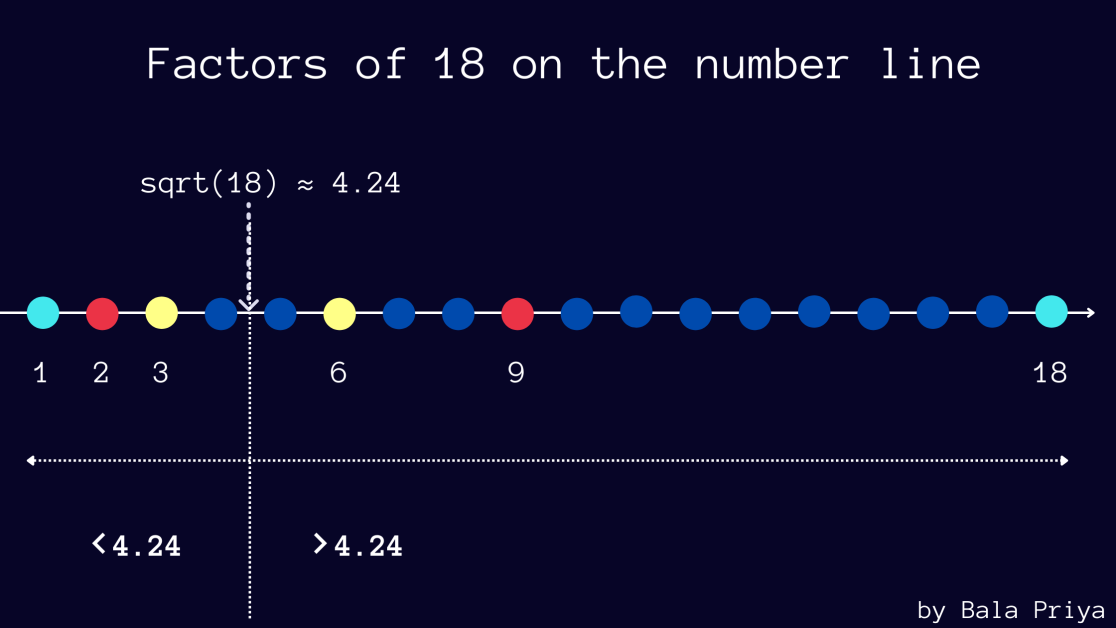
Se o número n for um quadrado perfeito, você terá a = b = √n como um dos fatores.
️ Veja os fatores de 36 na tabela abaixo. Como 36 é um quadrado perfeito, a = b = 6 é um dos fatores. Para todos os outros pares de fatores (a, b), a < 6 e b > 6 são válidos.
| uma | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
Resumindo, temos o seguinte:
- Todo número n pode ser escrito como n = axb
- Se n é um quadrado perfeito, então a = b = √n .
- E se a < b , então, a < √n e b > √n .
- Caso contrário, se a > b , então a > √n e b < √n .
Portanto, em vez de percorrer todos os inteiros até n/2, você pode optar por executar até √n. E isso é muito mais eficiente do que nossa abordagem anterior.
Como modificar o algoritmo is_prime() para O(√n)
Vamos continuar otimizando a função para verificar os números primos em Python.
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return TrueAgora, vamos analisar a definição da função acima:
- Para calcular a raiz quadrada de um número, vamos importar o módulo matemático embutido do Python e usar a função
math.sqrt(). - Como n pode não ser um quadrado perfeito, teremos que convertê-lo em um inteiro. Use
int(var)para convertervarem umint. - Para ter certeza de que estamos realmente verificando até √n, adicionamos um mais um, pois a função
range()exclui o ponto final do intervalo por padrão.
A célula de código abaixo verifica se nossa função is_prime() funciona corretamente.
is_prime(8) # False is_prime(15) # False is_prime(23) # TrueNa próxima seção, vamos criar alguns gráficos simples para entender O(n) e O(√n) visualmente.
Comparando O(n) e O(√n) Visualmente
️ Execute o seguinte trecho de código em um ambiente de notebook Jupyter de sua escolha.
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)O trecho acima mostra como você pode plotar as curvas para n e √n para um intervalo de valores.
- Usamos a função NumPy arange() para criar uma matriz de números.
- E então, coletamos os valores de n e √n até, mas não incluindo 20, em um DataFrame pandas.
- Em seguida, plotamos usando a função lineplot() do seaborn.
A partir do gráfico abaixo, vemos que √n é significativamente menor que n.
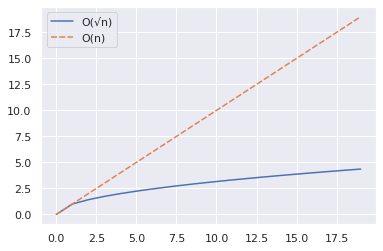
Vamos agora aumentar o intervalo para até 2000 e repetir os mesmos passos acima.
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 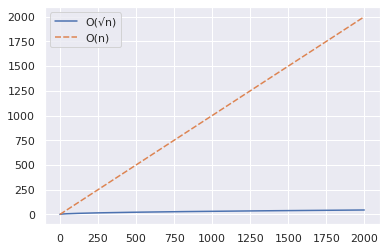
A partir do gráfico acima, você pode inferir que o algoritmo O(√n) é significativamente mais rápido quando você está testando se um número grande é primo.
Aqui está um exemplo rápido: 2377 é um número primo – verifique isso!
Enquanto a abordagem O(n) terá a ordem de 2.000 passos, o algoritmo O(√n) pode ajudar a chegar à resposta em apenas 49 passos.
Conclusão
E é hora de um resumo rápido.
- Para verificar se um número é primo, a abordagem ingênua é percorrer todos os números no intervalo (2, n-1). Se você não encontrar um fator que divida n, então n é primo.
- Como o único fator de n maior que n/2 é o próprio n, você pode optar por executar apenas até n/2.
- Ambas as abordagens acima têm uma complexidade de tempo de O(n).
- Como os fatores de um número ocorrem em pares, você pode executar apenas até √n. Este algoritmo é muito mais rápido que O(n). E o ganho é apreciável ao verificar se um número grande é primo ou não.
Espero que você entenda como verificar se um número é primo em Python. Como próximo passo, você pode conferir nosso tutorial sobre programas Python sobre operações com strings - onde você aprenderá a verificar se strings são palíndromos, anagramas e muito mais.
Vejo todos vocês em outro tutorial. Até lá, boa codificação!

