如何在 Python 中檢查一個數字是否為素數
已發表: 2022-05-02本教程將教您如何編寫 Python 程序來檢查數字是否為素數。
如果您曾經參加過編碼測試,那麼您會遇到關於素數測試或檢查數字是否為素數的數學問題。 在接下來的幾分鐘內,您將學會為這個問題提出最佳解決方案。
在本教程中,您將:
- 複習素數的基礎知識,
- 編寫 Python 代碼來檢查一個數是否為素數,以及
- 進一步優化它以獲得 O(√n) 運行時算法。
對於所有這些以及更多,讓我們開始吧。
什麼是質數?
讓我們從回顧素數的基礎開始。
在數論中,如果自然數n恰好具有兩個因數: 1和數字本身 ( n ),則稱它為素數。 回想一下你學校的數學:如果i整除n ,則數字i被稱為數字n的因數。
下表列出了一些數字、它們的所有因數以及它們是否為質數。
| n | 因素 | 是總理嗎? |
| 1 | 1 | 不 |
| 2 | 1, 2 | 是的 |
| 3 | 1、3 | 是的 |
| 4 | 1、2、4 | 不 |
| 7 | 1、7 | 是的 |
| 15 | 1、3、5、15 | 不 |
從上表中,我們可以寫出以下內容:
- 2是最小的素數。
- 1 是每個數字的因數。
- 每個數字
n都是它自己的一個因數。
所以 1 和 n 是任何數 n 的微不足道的因數。 素數不應該有這兩個以外的任何因素。
這意味著當您從 2 變為 n – 1 時,您應該無法找到一個將 n 整除而沒有餘數的非平凡因數。
在 Python 中檢查數字是否為素數的 O(n) 算法
在本節中,讓我們將上述方法形式化為 Python 函數。
您可以使用 Python 中的range()對象遍歷從 2 到 n – 1 的所有數字。
在 Python 中,
range(start, stop, step)返回一個範圍對象。 然後,您可以迭代 range 對像以獲取從start一直到stop -1的步驟step的序列。
由於我們需要從 2 到 n-1 的整數集合,我們可以指定range(2, n)並將其與for循環結合使用。
這是我們想做的事情:
- 如果你找到一個能將n整除而沒有餘數的數,你可以立即斷定這個數不是素數。
- 如果你遍歷了從2一直到n – 1的整個數字範圍,但沒有找到一個能將n整除的數字,那麼這個數字就是素數。
用於檢查素數的 Python 函數
使用上述內容,我們可以繼續定義函數is_prime()如下。
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return True現在讓我們解析上面的函數定義。
- 上面的函數
is_prime()接受一個正整數n作為參數。 - 如果您在 (2, n-1) 的指定範圍內找到一個因子,該函數將返回
False— 因為該數字不是素數。 - 如果您遍歷整個循環而沒有找到一個因素,它會返回
True。
接下來,讓我們用參數調用函數並驗證輸出是否正確。
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True 在上面的輸出中,您看到 2 和 11 是素數(函數返回True )。 並且 8 和 9 不是素數(函數返回False )。
如何優化 Python 函數 is_prime()
我們可以在這裡做一個小的優化。 請注意下表中的因素列表。
| 數字 | 因素 |
| 6 | 1、2、3、6 |
| 10 | 1、2、5、10 |
| 18 | 1、2、3、6、9、18 |
好吧,我們可以看到, n中唯一大於n/2的因子就是n本身。
所以這意味著您不必一直循環到 n – 1。您可以只運行循環到 n/2。
如果你在 n/2 之前沒有找到一個重要的因素,那麼你也找不到超過 n/2 的因素。
現在讓我們修改函數is_prime()以檢查 (2, n/2) 範圍內的因子
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return True讓我們繼續通過幾個函數調用來驗證輸出。
is_prime(9) # False is_prime(11) # True儘管看起來我們已經優化了,但就運行時復雜性而言,該算法並不比前一種算法更有效。 實際上,它們都具有O(n)運行時復雜度:與 n 的值成正比或與 n 成線性關係。
我們能做得更好嗎? 我們可以!
️ 繼續下一節以確定如何提高質數測試的時間複雜度。
在 Python 中檢查素數的 O(√n) 算法
碰巧一個數的因數成對出現。
如果a是數n的一個因數,那麼也存在一個因數b使得axb = n ,或者簡單地說, ab = n 。
讓我們通過一個例子來驗證這一點。

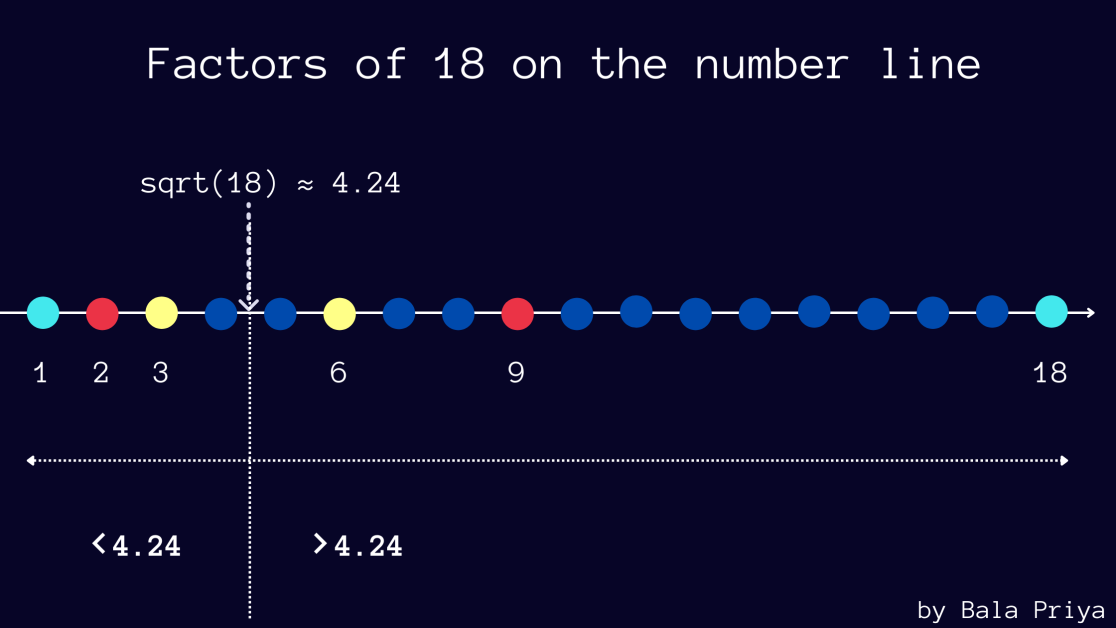
下表顯示了數字 18 成對出現的因素。 如果您願意,您可以再驗證幾個號碼。
另請注意,√18 約為 4.24。
在成對出現的因子(a, b)中,您可以看到如果a小於 4.24,則b大於 4.24——在本例中為 (2, 18) 和 (3, 6)。
| 一個 | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
下圖顯示了在數軸上繪製的 18 的因數。
如果數字 n 恰好是一個完美的正方形,那麼您將 a = b = √n 作為因素之一。
️看下表中36的因數。 由於 36 是一個完美的正方形,a = b = 6 是因素之一。 對於所有其他因子對 (a, b),a < 6 和 b > 6 成立。
| 一個 | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
總結起來,我們有以下幾點:
- 每個數n都可以寫成n = axb
- 如果n是完全平方,則a = b = √n 。
- 如果a < b ,則a < √n且b > √n 。
- 否則,如果a > b ,則a > √n且b < √n 。
因此,您可以選擇運行到 √n,而不是循環遍歷直到 n/2 的所有整數。 這比我們以前的方法效率高得多。
如何將 is_prime() 修改為 O(√n) 算法
讓我們繼續優化函數以檢查 Python 中的素數。
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return True現在,讓我們解析上面的函數定義:
- 要計算一個數字的平方根,讓我們導入 Python 的內置數學模塊,並使用
math.sqrt()函數。 - 由於n可能不是一個完美的正方形,我們必須將其轉換為整數。 使用
int(var)將var轉換為int。 - 為了確保我們實際上檢查到 √n,我們添加了一個加一,因為
range()函數默認排除了範圍的端點。
下面的代碼單元驗證我們的函數is_prime()是否正常工作。
is_prime(8) # False is_prime(15) # False is_prime(23) # True在下一節中,讓我們創建一些簡單的圖來直觀地理解 O(n) 和 O(√n)。
直觀地比較 O(n) 和 O(√n)
️ 在您選擇的 Jupyter 筆記本環境中運行以下代碼片段。
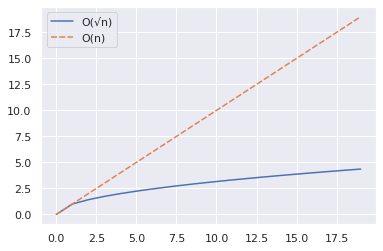
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)上面的代碼片段顯示瞭如何為一系列值繪製 n 和 √n 的曲線。
- 我們使用 NumPy arange() 函數來創建一個數字數組。
- 然後,我們將 n 和 √n 的值最多(但不包括 20)收集到 pandas DataFrame 中。
- 接下來,我們使用 seaborn 的 lineplot() 函數進行繪圖。
從下圖中,我們看到 √n 明顯小於 n。
現在讓我們將範圍增加到高達 2000 並重複與上述相同的步驟。
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 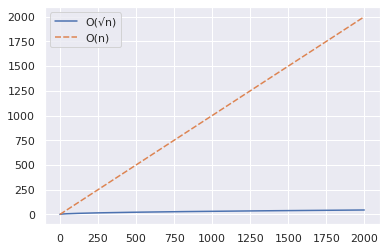
從上圖中,您可以推斷出 O(√n) 算法在測試大數是否為素數時明顯更快。
這是一個簡單的例子:2377 是一個素數——驗證一下!
雖然 O(n) 方法需要大約 2000 步,但 O(√n) 算法只需 49 步即可幫助得出答案。
結論
現在是快速總結的時候了。
- 要檢查一個數字是否為素數,最簡單的方法是遍歷 (2, n-1) 範圍內的所有數字。 如果你沒有找到除以 n 的因子,那麼 n 是素數。
- 由於 n 大於 n/2 的唯一因素是 n 本身,您可以選擇只運行到 n/2。
- 上述兩種方法的時間複雜度都是 O(n)。
- 由於數字的因數成對出現,因此您最多只能運行 √n。 這個算法比 O(n) 快很多。 當檢查一個大數是否是素數時,增益是可觀的。
我希望您了解如何在 Python 中檢查一個數字是否為素數。 下一步,您可以查看我們關於字符串操作的 Python 程序教程——您將在其中學習檢查字符串是否為回文、字謎等。
在另一個教程中見。 在那之前,快樂的編碼!
