Как проверить, является ли число простым в Python
Опубликовано: 2022-05-02В этом руководстве вы узнаете, как написать программу на Python для проверки, является ли число простым или нет.
Если вы когда-либо проходили тесты по программированию, вы сталкивались с математическим вопросом в тесте на простоту или на проверку того, является ли число простым. И в течение следующих нескольких минут вы научитесь придумывать оптимальное решение этого вопроса.
В этом уроке вы:
- повторить основы простых чисел,
- написать код Python, чтобы проверить, является ли число простым, и
- оптимизируйте его дальше, чтобы получить алгоритм времени выполнения O (√ n).
Для всего этого и многого другого, давайте начнем.
Что такое простое число?
Начнем с рассмотрения основ простых чисел.
В теории чисел натуральное число n называется простым , если оно имеет ровно два делителя : 1 и само число ( n ). Вспомните из школьной математики: говорят, что число i является делителем числа n , если i делит n без остатка.
В следующей таблице перечислены несколько чисел, все их множители и являются ли они простыми.
| н | Факторы | Прайм? |
| 1 | 1 | Нет |
| 2 | 1, 2 | Да |
| 3 | 1, 3 | Да |
| 4 | 1, 2, 4 | Нет |
| 7 | 1, 7 | Да |
| 15 | 1, 3, 5, 15 | Нет |
Из приведенной выше таблицы мы можем записать следующее:
- 2 — наименьшее простое число.
- 1 является множителем каждого числа.
- Каждое число
nсамо по себе является множителем.
Итак, 1 и n — тривиальные множители для любого числа n. И у простого числа не должно быть других делителей, кроме этих двух.
Это означает, что при переходе от 2 к n – 1 вы не сможете найти нетривиальный множитель, который делит n без остатка.
Алгоритм O (n) для проверки того, является ли число простым в Python
В этом разделе давайте формализуем описанный выше подход в виде функции Python.
Вы можете перебрать все числа от 2 до n – 1, используя объект range() в Python.
В Python
range(start, stop, step)возвращает объект диапазона. Затем вы можете выполнить итерацию по объекту диапазона, чтобы получить последовательность отstartдоstop -1в шагахstep.
Поскольку нам нужен набор целых чисел от 2 до n-1, мы можем указать range(2, n) и использовать его в сочетании с циклом for .
Вот что мы хотели бы сделать:
- Если вы найдете число, которое делит n нацело без остатка, вы можете сразу сделать вывод, что это число не простое.
- Если вы перебрали весь диапазон чисел от 2 до n – 1 и не нашли числа, которое делит n без остатка, то это число простое.
Функция Python для проверки простого числа
Используя вышеизложенное, мы можем пойти дальше и определить функцию is_prime() следующим образом.
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return TrueДавайте теперь разберем приведенное выше определение функции.
- Приведенная выше функция
is_prime()принимает в качестве аргумента положительное целое число n . - Если вы найдете множитель в указанном диапазоне (2, n-1), функция вернет
False, так как число не простое. - И он возвращает
True, если вы проходите весь цикл, не найдя множителя.
Далее давайте вызовем функцию с аргументами и проверим правильность вывода.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True В выводе выше вы видите, что 2 и 11 являются простыми (функция возвращает True ). И 8, и 9 не простые (функция возвращает False ).
Как оптимизировать функцию Python is_prime()
Мы можем сделать небольшую оптимизацию здесь. Обратите внимание на список факторов в таблице ниже.
| Число | Факторы |
| 6 | 1, 2, 3 , 6 |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
Итак, мы видим, что единственный множитель n , который больше n/2 , — это сам n .
Таким образом, это означает, что вам не нужно зацикливаться до n – 1. Вместо этого вы можете запускать цикл только до n/2.
Если вы не найдете нетривиальный множитель до n/2, вы не сможете найти и множитель выше n/2.
Теперь давайте изменим функцию is_prime() для проверки факторов в диапазоне (2, n/2)
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return TrueДавайте продолжим и проверим вывод с помощью нескольких вызовов функций.
is_prime(9) # False is_prime(11) # TrueХотя может показаться, что мы оптимизировали, этот алгоритм не эффективнее предыдущего с точки зрения сложности выполнения. На самом деле, они оба имеют сложность выполнения O(n) : пропорциональную значению n или линейную по n.
Можем ли мы сделать лучше? Да мы можем!
️ Перейдите к следующему разделу, чтобы определить, как улучшить временную сложность тестирования простых чисел.
Алгоритм O(√n) для проверки простого числа в Python
Бывает, что множители числа встречаются парами.
Если a является множителем числа n , то также существует множитель b такой, что axb = n , или просто ab = n .
Давайте проверим это на примере.
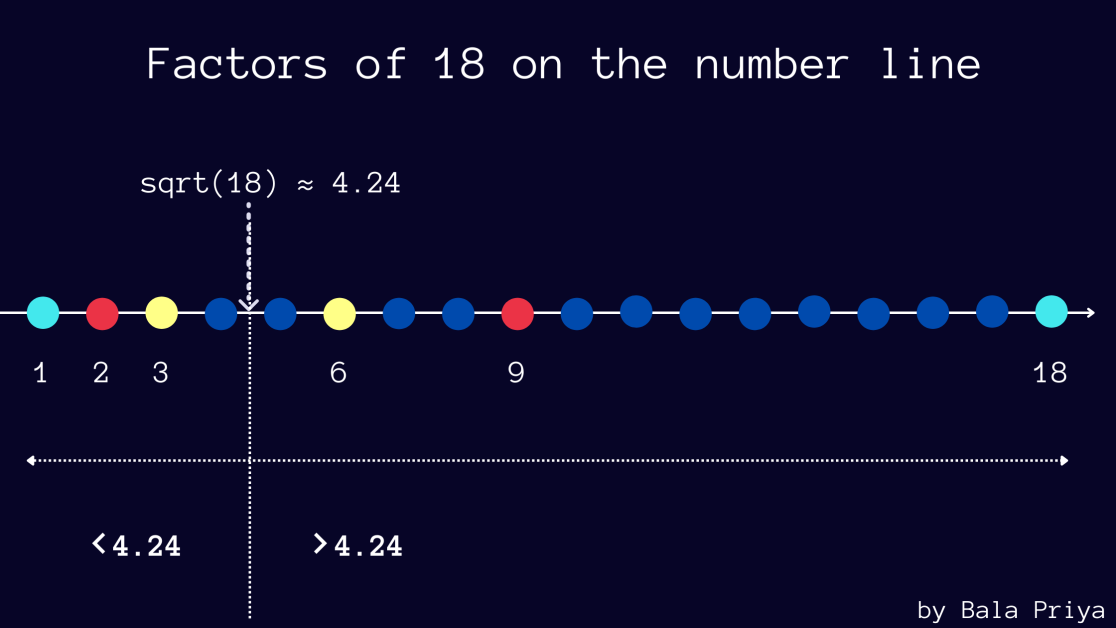
В таблице ниже показаны множители числа 18, встречающиеся парами. Вы можете проверить то же самое для еще нескольких номеров, если хотите.
Также обратите внимание, что √18 примерно равно 4,24.
А среди множителей, встречающихся в парах (a, b) , видно, что если a меньше 4,24, то b больше 4,24 — в этом примере (2, 18) и (3, 6).
| а | б |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
На рисунке ниже показаны множители 18, нанесенные на числовую прямую.
Если число n является полным квадратом, вы будете иметь a = b = √n в качестве одного из множителей.
️ Посмотрите на множители 36 в таблице ниже. Поскольку 36 — полный квадрат, a = b = 6 — один из множителей. Для всех остальных пар факторов (a, b) выполняется a < 6 и b > 6.
| а | б |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
Подводя итог, имеем следующее:
- Каждое число n можно записать как n = axb
- Если n — полный квадрат, то a = b = √n .
- А если a < b , то a < √n и b > √n .
- В противном случае, если a > b , то a > √n и b < √n .
Таким образом, вместо того, чтобы перебирать все целые числа до n/2, вы можете выбрать до √n. И это намного эффективнее, чем наш предыдущий подход.
Как изменить алгоритм is_prime() на O(√n)
Приступим к оптимизации функции для проверки простых чисел в Python.
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return TrueТеперь давайте разберем приведенное выше определение функции:
- Чтобы вычислить квадратный корень числа, давайте импортируем встроенный математический модуль Python и используем
math.sqrt(). - Поскольку n не может быть идеальным квадратом, нам придется привести его к целому числу. Используйте
int(var)для преобразованияvarвint. - Чтобы убедиться, что мы действительно проверяем до √n, мы добавляем плюс один, поскольку функция
range()по умолчанию исключает конечную точку диапазона.
Ячейка кода ниже подтверждает, что наша функция is_prime() работает правильно.
is_prime(8) # False is_prime(15) # False is_prime(23) # TrueВ следующем разделе давайте создадим несколько простых графиков, чтобы визуально понять O (n) и O (√ n).
Визуальное сравнение O(n) и O(√n)
️ Запустите следующий фрагмент кода в выбранной вами среде ноутбука Jupyter.
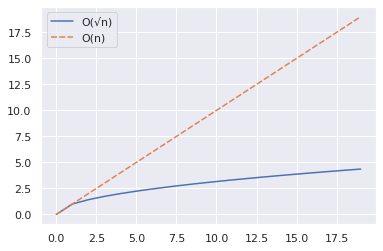
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)В приведенном выше фрагменте показано, как можно построить кривые для n и √n для диапазона значений.
- Мы используем функцию NumPy arange() для создания массива чисел.
- Затем мы собираем значения n и √n до 20, но не включая их, в кадр данных pandas.
- Затем мы строим график, используя функцию lineplot() Seaborn.
Из графика ниже видно, что √n значительно меньше n.
Давайте теперь увеличим диапазон до 2000 и повторим те же шаги, что и выше.
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 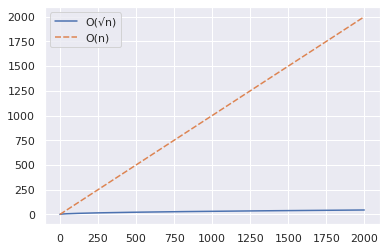
Из приведенного выше графика можно сделать вывод, что алгоритм O(√n) работает значительно быстрее, когда вы проверяете, является ли большое число простым.
Вот быстрый пример: 2377 — простое число — проверьте это!
В то время как подход O(n) потребует порядка 2000 шагов, алгоритм O(√n) поможет получить ответ всего за 49 шагов.
Вывод
И пришло время для краткого обзора.
- Чтобы проверить, является ли число простым, наивный подход состоит в том, чтобы перебрать все числа в диапазоне (2, n-1). Если вы не найдете множитель, который делит n, то n — простое число.
- Поскольку единственный множитель n, превышающий n/2, — это само n, вы можете работать только до n/2.
- Оба вышеупомянутых подхода имеют временную сложность O (n).
- Поскольку множители числа встречаются парами, вы можете работать только до √n. Этот алгоритм намного быстрее, чем O (n). И выигрыш заметен при проверке, является ли большое число простым или нет.
Надеюсь, вы понимаете, как проверить, является ли число простым в Python. В качестве следующего шага вы можете ознакомиться с нашим учебным пособием по программам на Python, посвященным операциям со строками, где вы научитесь проверять, являются ли строки палиндромами, анаграммами и т. д.
Увидимся в другом уроке. А пока удачного кодирования!

