如何在 Python 中检查一个数字是否为素数
已发表: 2022-05-02本教程将教您如何编写 Python 程序来检查数字是否为素数。
如果您曾经参加过编码测试,那么您会遇到关于素数测试或检查数字是否为素数的数学问题。 在接下来的几分钟内,您将学会为这个问题提出最佳解决方案。
在本教程中,您将:
- 复习素数的基础知识,
- 编写 Python 代码来检查一个数是否为素数,以及
- 进一步优化它以获得 O(√n) 运行时算法。
对于所有这些以及更多,让我们开始吧。
什么是质数?
让我们从回顾素数的基础开始。
在数论中,如果自然数n恰好具有两个因数: 1和数字本身 ( n ),则称它为素数。 回想一下你学校的数学:如果i整除n ,则数字i被称为数字n的因数。
下表列出了一些数字、它们的所有因数以及它们是否为质数。
| n | 因素 | 是总理吗? |
| 1 | 1 | 不 |
| 2 | 1, 2 | 是的 |
| 3 | 1、3 | 是的 |
| 4 | 1、2、4 | 不 |
| 7 | 1、7 | 是的 |
| 15 | 1、3、5、15 | 不 |
从上表中,我们可以写出以下内容:
- 2是最小的素数。
- 1 是每个数字的因数。
- 每个数字
n都是它自己的一个因数。
所以 1 和 n 是任何数 n 的微不足道的因数。 素数不应该有这两个以外的任何因素。
这意味着当您从 2 变为 n – 1 时,您应该无法找到将 n 整除而没有余数的重要因子。
在 Python 中检查数字是否为素数的 O(n) 算法
在本节中,让我们将上述方法形式化为 Python 函数。
您可以使用 Python 中的range()对象遍历从 2 到 n – 1 的所有数字。
在 Python 中,
range(start, stop, step)返回一个范围对象。 然后,您可以迭代 range 对象以获取从start一直到stop -1的步骤step的序列。
由于我们需要从 2 到 n-1 的整数集合,我们可以指定range(2, n)并将其与for循环结合使用。
这是我们想做的事情:
- 如果你找到一个能将n整除而没有余数的数,你可以立即断定这个数不是素数。
- 如果你遍历了从2一直到n – 1的整个数字范围,但没有找到一个能将n整除的数字,那么这个数字就是素数。
用于检查素数的 Python 函数
使用上述内容,我们可以继续定义函数is_prime()如下。
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return True现在让我们解析上面的函数定义。
- 上面的函数
is_prime()接受一个正整数n作为参数。 - 如果您在 (2, n-1) 的指定范围内找到一个因子,该函数将返回
False— 因为该数字不是素数。 - 如果您遍历整个循环而没有找到一个因素,它会返回
True。
接下来,让我们用参数调用函数并验证输出是否正确。
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True 在上面的输出中,您看到 2 和 11 是素数(函数返回True )。 并且 8 和 9 不是素数(函数返回False )。
如何优化 Python 函数 is_prime()
我们可以在这里做一个小的优化。 请注意下表中的因素列表。
| 数字 | 因素 |
| 6 | 1、2、3、6 |
| 10 | 1、2、5、10 |
| 18 | 1、2、3、6、9、18 |
好吧,我们可以看到, n中唯一大于n/2的因子就是n本身。
所以这意味着您不必一直循环到 n – 1。您可以只运行循环到 n/2。
如果你在 n/2 之前没有找到一个重要的因素,那么你也找不到超过 n/2 的因素。
现在让我们修改函数is_prime()以检查 (2, n/2) 范围内的因子
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return True让我们继续通过几个函数调用来验证输出。
is_prime(9) # False is_prime(11) # True尽管看起来我们已经优化了,但就运行时复杂性而言,该算法并不比前一种算法更有效。 实际上,它们都具有O(n)运行时复杂度:与 n 的值成正比或与 n 成线性关系。
我们能做得更好吗? 我们可以!
️ 继续下一节以确定如何提高质数测试的时间复杂度。
在 Python 中检查素数的 O(√n) 算法
碰巧一个数的因数成对出现。
如果a是数n的一个因数,那么也存在一个因数b使得axb = n ,或者简单地说, ab = n 。
让我们通过一个例子来验证这一点。

下表显示了数字 18 成对出现的因素。 如果您愿意,您可以再验证几个号码。
另请注意,√18 约为 4.24。
在成对出现的因子(a, b)中,您可以看到如果a小于 4.24,则b大于 4.24——在本例中为 (2, 18) 和 (3, 6)。
| 一个 | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
下图显示了在数轴上绘制的 18 的因数。
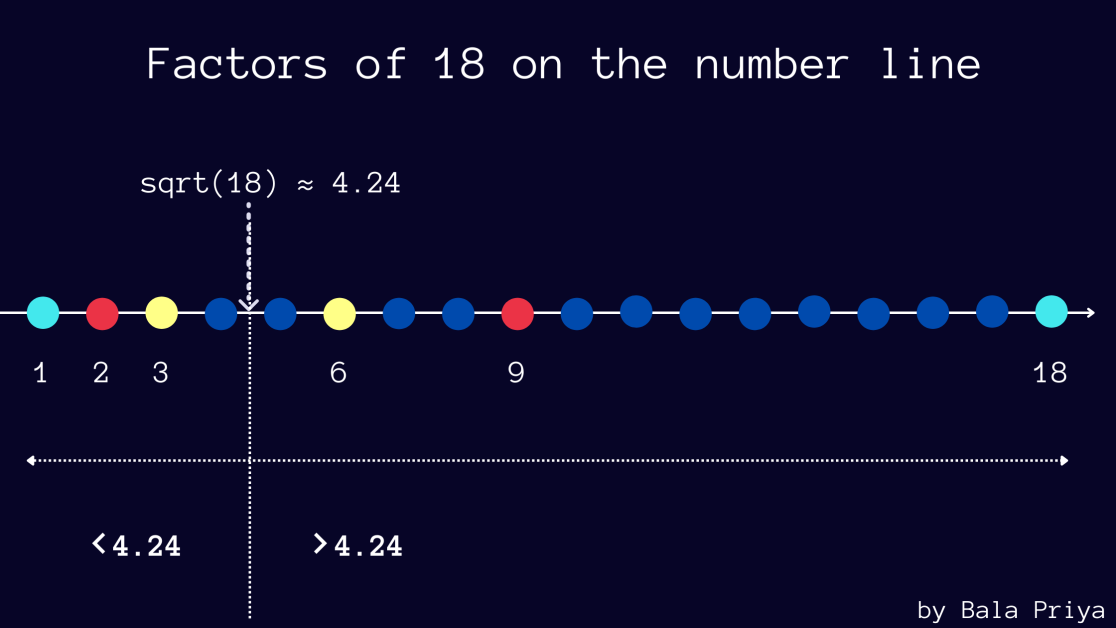
如果数字 n 恰好是一个完美的正方形,那么您将 a = b = √n 作为因素之一。
️看下表中36的因数。 由于 36 是一个完美的正方形,a = b = 6 是因素之一。 对于所有其他因子对 (a, b),a < 6 和 b > 6 成立。
| 一个 | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
总结起来,我们有以下几点:
- 每个数n都可以写成n = axb
- 如果n是完全平方,则a = b = √n 。
- 如果a < b ,则a < √n且b > √n 。
- 否则,如果a > b ,则a > √n且b < √n 。
因此,您可以选择运行到 √n,而不是循环遍历直到 n/2 的所有整数。 这比我们以前的方法效率高得多。
如何将 is_prime() 修改为 O(√n) 算法
让我们继续优化函数以检查 Python 中的素数。
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return True现在,让我们解析上面的函数定义:
- 要计算一个数字的平方根,让我们导入 Python 的内置数学模块,并使用
math.sqrt()函数。 - 由于n可能不是一个完美的正方形,我们必须将其转换为整数。 使用
int(var)将var转换为int。 - 为了确保我们实际上检查到 √n,我们添加了一个加一,因为
range()函数默认排除了范围的端点。
下面的代码单元验证我们的函数is_prime()是否正常工作。
is_prime(8) # False is_prime(15) # False is_prime(23) # True在下一节中,让我们创建一些简单的图来直观地理解 O(n) 和 O(√n)。
直观地比较 O(n) 和 O(√n)
️ 在您选择的 Jupyter 笔记本环境中运行以下代码片段。
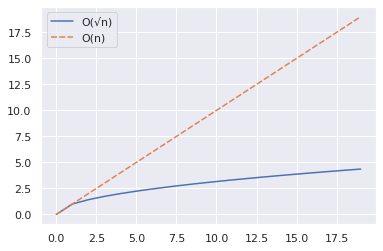
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)上面的代码片段显示了如何为一系列值绘制 n 和 √n 的曲线。
- 我们使用 NumPy arange() 函数来创建一个数字数组。
- 然后,我们将 n 和 √n 的值最多(但不包括 20)收集到 pandas DataFrame 中。
- 接下来,我们使用 seaborn 的 lineplot() 函数进行绘图。
从下图中,我们看到 √n 明显小于 n。
现在让我们将范围增加到高达 2000 并重复与上述相同的步骤。
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 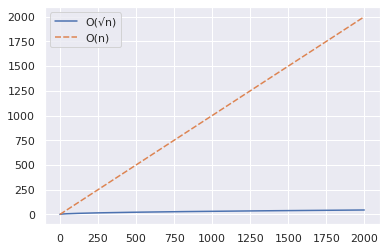
从上图中,您可以推断出 O(√n) 算法在测试大数是否为素数时明显更快。
这是一个简单的例子:2377 是一个素数——验证一下!
虽然 O(n) 方法需要大约 2000 步,但 O(√n) 算法只需 49 步即可帮助得出答案。
结论
现在是快速总结的时候了。
- 要检查一个数字是否为素数,最简单的方法是遍历 (2, n-1) 范围内的所有数字。 如果你没有找到除以 n 的因子,那么 n 是素数。
- 由于 n 大于 n/2 的唯一因素是 n 本身,您可以选择只运行到 n/2。
- 上述两种方法的时间复杂度都是 O(n)。
- 由于数字的因数成对出现,因此您最多只能运行 √n。 这个算法比 O(n) 快很多。 当检查一个大数是否是素数时,增益是可观的。
我希望您了解如何在 Python 中检查一个数字是否为素数。 下一步,您可以查看我们关于字符串操作的 Python 程序教程——您将在其中学习检查字符串是否为回文、字谜等。
在另一个教程中见。 在那之前,快乐的编码!
