Come verificare se un numero è primo in Python
Pubblicato: 2022-05-02Questo tutorial ti insegnerà come scrivere un programma Python per verificare se un numero è primo o meno.
Se hai mai sostenuto i test di codifica, ti sarai imbattuto nella domanda di matematica sul test per la primalità o per verificare se un numero è primo. E nei prossimi minuti imparerai a trovare la soluzione ottimale a questa domanda.
In questo tutorial, dovrai:
- rivedere le basi dei numeri primi,
- scrivi il codice Python per verificare se un numero è primo e
- ottimizzalo ulteriormente per ottenere un algoritmo di runtime O(√n).
Per tutto questo e altro, iniziamo.
Cos'è un numero primo?
Iniziamo esaminando le basi dei numeri primi.
Nella teoria dei numeri, un numero naturale n si dice primo se ha esattamente due fattori : 1 e il numero stesso ( n ). Ricorda dalla matematica della tua scuola: si dice che un numero i è un fattore del numero n , se i divide n equamente.
La tabella seguente elenca alcuni numeri, tutti i loro fattori e se sono primi.
| n | Fattori | Prime è? |
| 1 | 1 | No |
| 2 | 1, 2 | sì |
| 3 | 1, 3 | sì |
| 4 | 1, 2, 4 | No |
| 7 | 1, 7 | sì |
| 15 | 1, 3, 5, 15 | No |
Dalla tabella sopra, possiamo scrivere quanto segue:
- 2 è il numero primo più piccolo.
- 1 è un fattore di ogni numero.
- Ogni numero
nè un fattore di per sé.
Quindi 1 e n sono fattori banali per qualsiasi numero n. E un numero primo non dovrebbe avere altri fattori oltre a questi due.
Ciò significa che quando si passa da 2 a n – 1, non si dovrebbe essere in grado di trovare un fattore non banale che divida n senza resto.
O(n) Algoritmo per verificare se un numero è primo in Python
In questa sezione, formalizziamo l'approccio sopra in una funzione Python.
Puoi scorrere tutti i numeri da 2 a n – 1 usando l'oggetto range() in Python.
In Python,
range(start, stop, step)restituisce un oggetto range. È quindi possibile scorrere l'oggetto intervallo per ottenere una sequenzastartfinostop -1nei passaggi delstep.
Poiché abbiamo bisogno dell'insieme di interi da 2 a n-1, possiamo specificare range(2, n) e usarlo insieme a ciclo for .
Ecco cosa vorremmo fare:
- Se trovi un numero che divide n equamente senza resto, puoi immediatamente concludere che il numero non è primo.
- Se hai percorso l'intero intervallo di numeri da 2 fino a n – 1 senza trovare un numero che divida n equamente, allora il numero è primo.
Funzione Python per verificare il numero primo
Usando quanto sopra, possiamo andare avanti e definire la funzione is_prime() come segue.
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return TrueAnalizziamo ora la definizione della funzione sopra.
- La funzione precedente
is_prime()accetta un intero positivo n come argomento. - Se trovi un fattore nell'intervallo specificato di (2, n-1), la funzione restituisce
False, poiché il numero non è primo. - E restituisce
Truese si attraversa l'intero ciclo senza trovare un fattore.
Quindi, chiamiamo la funzione con argomenti e verifichiamo se l'output è corretto.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True Nell'output sopra, vedi che 2 e 11 sono primi (la funzione restituisce True ). E 8 e 9 non sono primi (la funzione restituisce False ).
Come ottimizzare la funzione Python is_prime()
Possiamo fare una piccola ottimizzazione qui. Osservare l'elenco dei fattori nella tabella seguente.
| Numero | Fattori |
| 6 | 1, 2, 3 , 6 |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
Bene, possiamo vedere che l'unico fattore di n maggiore di n/2 è n stesso.
Quindi questo significa che non devi eseguire il loop fino a n – 1. Puoi invece eseguire il loop solo fino a n/2.
Se non trovi un fattore non banale fino a n/2, non puoi trovarne nemmeno uno oltre n/2.
Ora modifichiamo la funzione is_prime() per verificare la presenza di fattori nell'intervallo (2, n/2)
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return TrueAndiamo avanti e verifichiamo l'output tramite alcune chiamate di funzione.
is_prime(9) # False is_prime(11) # TrueAnche se può sembrare che abbiamo ottimizzato, questo algoritmo non è più efficiente del precedente in termini di complessità di runtime. Infatti, entrambi hanno O(n) complessità di runtime: proporzionale al valore di n o lineare in n.
Possiamo fare di meglio? Sì possiamo!
️ Passare alla sezione successiva per determinare come migliorare la complessità temporale per il test dei numeri primi.
Algoritmo O(√n) per verificare il numero primo in Python
Succede che i fattori di un numero si verificano in coppia.
Se a è un fattore del numero n , allora esiste anche un fattore b tale che axb = n , o semplicemente ab = n .
Verifichiamolo attraverso un esempio.
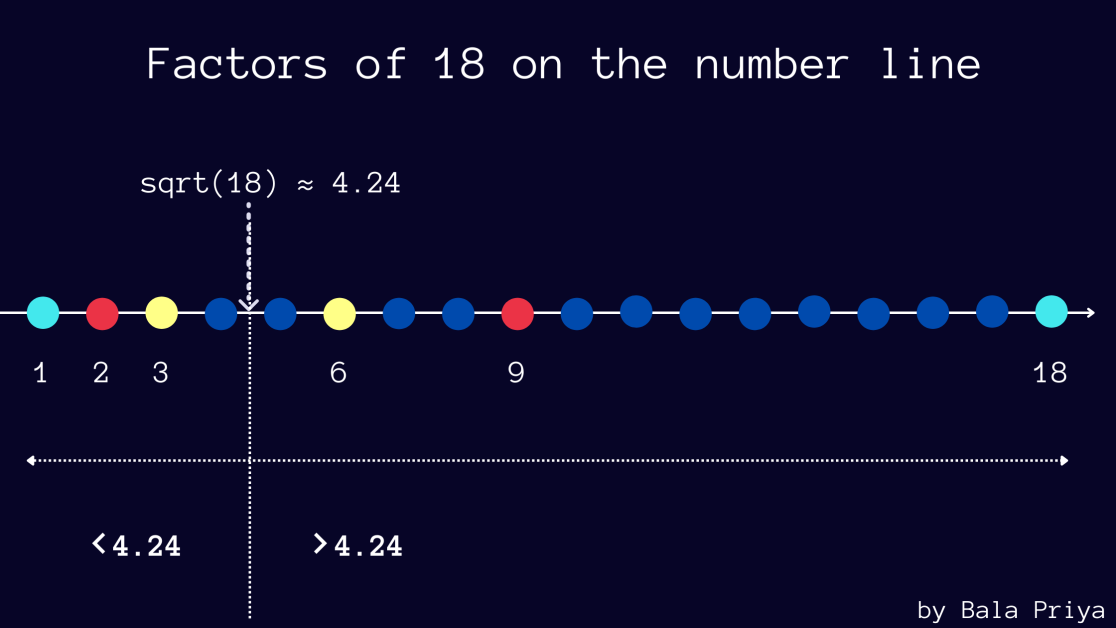
La tabella seguente mostra i fattori del numero 18 che si verificano in coppia. Puoi verificare lo stesso per qualche numero in più, se lo desideri.
Inoltre, si noti che √18 è circa 4,24.
E nei fattori che si verificano in coppia (a, b) , puoi vedere che se a è inferiore a 4,24, allora b è maggiore di 4,24, in questo esempio (2, 18) e (3, 6).
| un | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
La figura seguente mostra i fattori di 18 tracciati sulla linea dei numeri.
Se il numero n è un quadrato perfetto, avrai a = b = √n come uno dei fattori.
️ Guarda i fattori di 36 nella tabella seguente. Poiché 36 è un quadrato perfetto, a = b = 6 è uno dei fattori. Per tutte le altre coppie di fattori (a, b), vale a < 6 e b > 6.
| un | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
Riassumendo, abbiamo quanto segue:
- Ogni numero n può essere scritto come n = axb
- Se n è un quadrato perfetto, allora a = b = √n .
- E se a < b , allora a < √n e b > √n .
- Altrimenti, se a > b , allora a > √n e b < √n .
Quindi, invece di scorrere tutti gli interi fino a n/2, puoi scegliere di eseguire fino a √n. E questo è molto più efficiente del nostro approccio precedente.
Come modificare l'algoritmo is_prime() in O(√n).
Procediamo con l'ottimizzazione della funzione per verificare la presenza di numeri primi in Python.
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return TrueOra, analizziamo la definizione della funzione sopra:
- Per calcolare la radice quadrata di un numero, importiamo il modulo matematico integrato in Python e usiamo la funzione
math.sqrt(). - Poiché n potrebbe non essere un quadrato perfetto, dovremo trasformarlo in un numero intero. Usa
int(var)per eseguire il cast divarin unint. - Per assicurarci di controllare effettivamente fino a √n, aggiungiamo uno più uno poiché la funzione
range()esclude l'endpoint dell'intervallo per impostazione predefinita.
La cella di codice sottostante verifica che la nostra funzione is_prime() funzioni correttamente.
is_prime(8) # False is_prime(15) # False is_prime(23) # TrueNella prossima sezione, creiamo alcuni semplici grafici per comprendere visivamente O(n) e O(√n).
Confronto visivo di O(n) e O(√n).
️ Esegui il seguente frammento di codice in un ambiente notebook Jupyter a tua scelta.
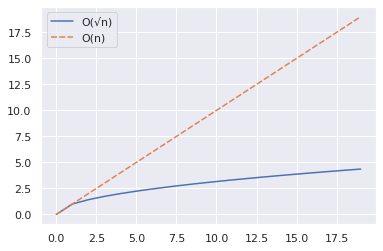
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)Il frammento di cui sopra mostra come puoi tracciare le curve per n e √n per un intervallo di valori.
- Usiamo la funzione NumPy arange() per creare una matrice di numeri.
- E poi, raccogliamo i valori di n e √n fino a, ma escluso 20, in un DataFrame panda.
- Successivamente, tracciamo usando la funzione lineplot() di seaborn.
Dal grafico sottostante, vediamo che √n è significativamente minore di n.
Ora aumentiamo l'intervallo fino a 2000 e ripetiamo gli stessi passaggi di cui sopra.
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 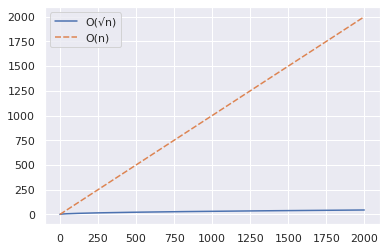
Dal grafico sopra, puoi dedurre che l'algoritmo O(√n) è significativamente più veloce quando stai testando se un numero grande è primo.
Ecco un rapido esempio: 2377 è un numero primo: verificalo!
Mentre l'approccio O(n) prenderà l'ordine di 2000 passi, l'algoritmo O(√n) può aiutare ad arrivare alla risposta in soli 49 passi.
Conclusione
Ed è tempo di un breve riassunto.
- Per verificare se un numero è primo, l'approccio ingenuo è quello di scorrere tutti i numeri nell'intervallo (2, n-1). Se non trovi un fattore che divide n, allora n è primo.
- Poiché l'unico fattore di n maggiore di n/2 è n stesso, puoi scegliere di eseguire solo fino a n/2.
- Entrambi gli approcci di cui sopra hanno una complessità temporale di O(n).
- Poiché i fattori di un numero si verificano in coppia, è possibile eseguire solo fino a √n. Questo algoritmo è molto più veloce di O(n). E il guadagno è apprezzabile quando si controlla se un numero grande è primo o meno.
Spero che tu capisca come verificare se un numero è primo in Python. Come passaggio successivo, puoi dare un'occhiata al nostro tutorial sui programmi Python sulle operazioni sulle stringhe, dove imparerai a verificare se le stringhe sono palindromi, anagrammi e altro.
Ci vediamo tutti in un altro tutorial. Fino ad allora, buona programmazione!

