Pythonで数値が素数であるかどうかを確認する方法
公開: 2022-05-02このチュートリアルでは、Pythonプログラムを作成して、数値が素数であるかどうかを確認する方法を説明します。
コーディングテストを行ったことがある場合は、素数性のテストで数学の質問に出くわしたり、数値が素数であるかどうかを確認したりします。 そして、次の数分で、この質問に対する最適な解決策を考え出すことを学びます。
このチュートリアルでは、次のことを行います。
- 素数の基本を確認し、
- 数が素数であるかどうかを確認するPythonコードを記述し、
- さらに最適化して、O(√n)ランタイムアルゴリズムを取得します。
これ以上のことについて、始めましょう。
素数とは何ですか?
素数の基本を復習することから始めましょう。
数論では、自然数nは、 1と数自体( n )の2つの因子がある場合に素数と呼ばれます。 あなたの学校の数学を思い出してください。私がnを均等に割ると、数iは数nの因数であると言われます。
次の表に、いくつかの数値、それらのすべての要因、およびそれらが素数であるかどうかを示します。
| n | 要因 | プライムですか? |
| 1 | 1 | いいえ |
| 2 | 1、2 | はい |
| 3 | 1、3 | はい |
| 4 | 1、2、4 | いいえ |
| 7 | 1、7 | はい |
| 15 | 1、3、5、15 | いいえ |
上記の表から、次のように書き留めることができます。
- 2は最小の素数です。
- 1はすべての数の因数です。
- すべての数
nはそれ自体の要因です。
したがって、1とnは、任意の数nの自明な因子です。 そして、素数はこれら2つ以外の要素を持つべきではありません。
これは、2からn – 1に移動するときに、余りなしでnを除算する自明でない要素を見つけることができないはずであることを意味します。
Pythonで数値が素数であるかどうかを確認するO(n)アルゴリズム
このセクションでは、上記のアプローチをPython関数に形式化してみましょう。
Pythonのrange()オブジェクトを使用して、2からn –1までのすべての数値をループできます。
Pythonでは、
range(start, stop, step)は範囲オブジェクトを返します。 次に、範囲オブジェクトを反復処理して、ステップのstepでstartからstop -1までのシーケンスを取得できます。
2からn-1までの整数のセットが必要なので、 range(2, n)を指定して、 forループと組み合わせて使用できます。
これが私たちがやりたいことです:
- 余りなしでnを均等に分割する数を見つけた場合、その数は素数ではないとすぐに結論付けることができます。
- nを均等に分割する数を見つけずに、 2からn – 1までの数の全範囲をループした場合、その数は素数です。
素数をチェックするPython関数
上記を使用して、先に進み、関数is_prime()を次のように定義できます。
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return True上記の関数定義を解析してみましょう。
- 上記の関数
is_prime()は、引数として正の整数nを取ります。 - (2、n-1)の指定された範囲内の因子が見つかった場合、関数は
Falseを返します—数値は素数ではないためです。 - また、因子を見つけずにループ全体をトラバースすると、
Trueが返されます。
次に、引数を使用して関数を呼び出し、出力が正しいかどうかを確認しましょう。
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True 上記の出力では、2と11が素数であることがわかります(関数はTrueを返します)。 また、8と9は素数ではありません(関数はFalseを返します)。
Python関数を最適化する方法is_prime()
ここで小さな最適化を行うことができます。 以下の表の要因のリストを確認してください。
| 番号 | 要因 |
| 6 | 1、2、3、6 |
| 10 | 1、2、5、10 |
| 18 | 1、2、3、6、9、18 |
さて、 n /2より大きいnの唯一の要因はn自体であることがわかります。
つまり、n – 1までループする必要はありません。代わりに、n/2までしかループを実行できません。
n / 2まで自明でない要素が見つからない場合は、n/2を超える要素も見つけることができません。
次に、関数is_prime()を変更して、範囲(2、n / 2)の係数をチェックしましょう。
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return True先に進んで、いくつかの関数呼び出しを介して出力を確認しましょう。
is_prime(9) # False is_prime(11) # True最適化したように見えるかもしれませんが、このアルゴリズムは、実行時の複雑さの点で前のアルゴリズムよりも効率的ではありません。 実際、どちらも実行時の複雑さはO(n)です。つまり、nの値に比例するか、nの線形です。
もっと上手くできますか? はい、できます!
️次のセクションに進んで、素数テストの時間計算量を改善する方法を決定します。
Pythonで素数をチェックするO(√n)アルゴリズム
数の因数がペアで発生することが起こります。
aが数nの因数である場合、 axb = n 、または単にab=nとなる因数bも存在します。
例を通してこれを確認しましょう。

次の表は、ペアで発生する番号18の要因を示しています。 必要に応じて、さらにいくつかの番号について同じことを確認できます。
また、√18は約4.24であることに注意してください。
また、ペア(a、b)で発生する要因では、 aが4.24未満の場合、 bは4.24より大きいことがわかります。この例では、(2、18)と(3、6)です。
| a | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
下の図は、数直線上にプロットされた18の因数を示しています。
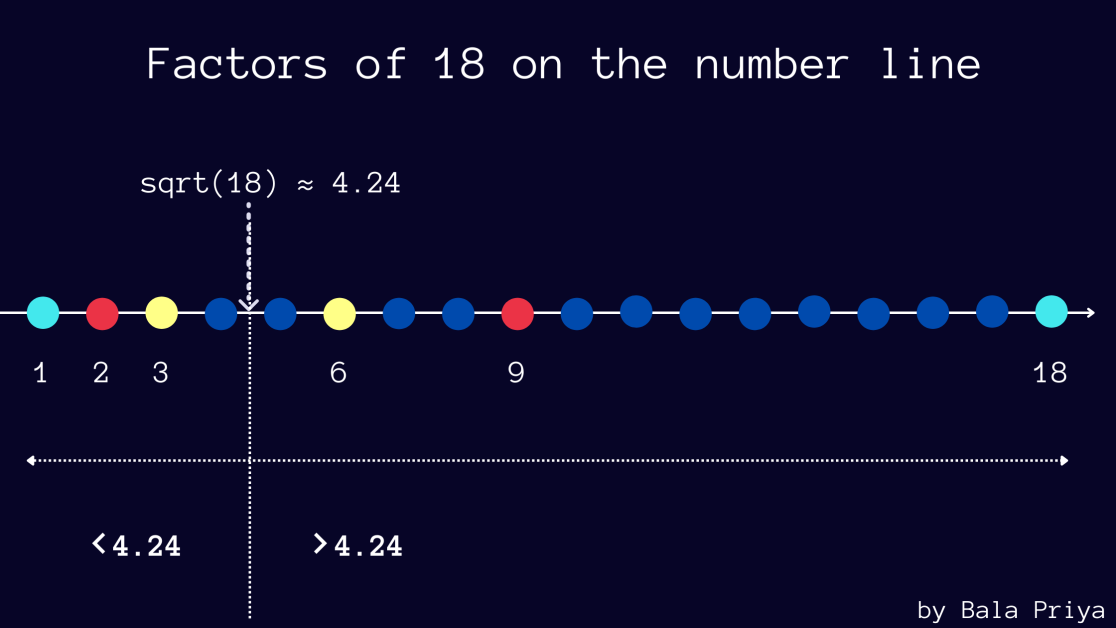
数nがたまたま完全な正方形である場合、要因の1つとしてa =b=√nがあります。
️下の表の36の係数を見てください。 36は完全な正方形であるため、a = b=6が要因の1つです。 他のすべての因子ペア(a、b)の場合、a<6およびb>6が成り立ちます。
| a | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
要約すると、次のようになります。
- すべての数nはn=axbと書くことができます
- nが完全な正方形の場合、 a =b=√nです。
- そして、 a <bの場合、 a<√nおよびb>√n 。
- それ以外の場合、a> bの場合、 a>√nおよびb<√n 。
したがって、n / 2までのすべての整数をループする代わりに、√nまで実行することを選択できます。 そして、これは以前のアプローチよりもはるかに効率的です。
is_prime()をO(√n)アルゴリズムに変更する方法
Pythonで素数をチェックする関数の最適化に進みましょう。
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return Trueそれでは、上記の関数定義を解析してみましょう。
- 数値の平方根を計算するには、Pythonの組み込みの数学モジュールをインポートし、
math.sqrt()関数を使用してみましょう。 - nは完全な正方形ではない可能性があるため、整数にキャストする必要があります。
int(var)を使用して、varをintにキャストします。 - 実際に√nまでチェックしていることを確認するために、
range()関数がデフォルトで範囲のエンドポイントを除外するため、プラス1を追加します。
以下のコードセルは、関数is_prime()が正しく機能することを確認します。
is_prime(8) # False is_prime(15) # False is_prime(23) # True次のセクションでは、O(n)とO(√n)を視覚的に理解するための簡単なプロットをいくつか作成しましょう。
O(n)とO(√n)を視覚的に比較する
️選択したJupyterノートブック環境で次のコードスニペットを実行します。
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)上記のスニペットは、ある範囲の値についてnと√nの曲線をプロットする方法を示しています。
- NumPy arange()関数を使用して、数値の配列を作成します。
- 次に、20までのnと√nの値をパンダのDataFrameに収集します。
- 次に、seabornのlineplot()関数を使用してプロットします。
以下のプロットから、√nがnよりも大幅に小さいことがわかります。
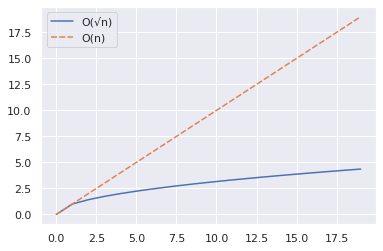
ここで、範囲を2000まで増やして、上記と同じ手順を繰り返します。
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 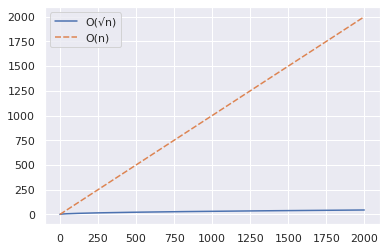
上記のプロットから、多数が素数であるかどうかをテストする場合、O(√n)アルゴリズムが大幅に高速であることが推測できます。
簡単な例を次に示します。2377は素数です。これを確認してください。
O(n)アプローチは2000ステップのオーダーを取りますが、O(√n)アルゴリズムはわずか49ステップで答えに到達するのに役立ちます。
結論
そして、簡単な要約の時間です。
- 数が素数であるかどうかを確認するための単純なアプローチは、範囲(2、n-1)のすべての数をループすることです。 nを分割する係数が見つからない場合は、nが素数です。
- n / 2より大きいnの唯一の要因はn自体であるため、n/2までのみ実行することを選択できます。
- 上記のアプローチは両方とも、O(n)の時間計算量を持っています。
- 数の要因はペアで発生するため、実行できるのは√nまでです。 このアルゴリズムは、O(n)よりもはるかに高速です。 そして、多数が素数であるかどうかをチェックするとき、ゲインはかなりのものです。
Pythonで数が素数であるかどうかを確認する方法を理解していただければ幸いです。 次のステップとして、文字列操作に関するPythonプログラムのチュートリアルを確認できます。ここでは、文字列が回文、アナグラムなどであるかどうかを確認する方法を学びます。
別のチュートリアルでお会いしましょう。 それまでは、コーディングを楽しんでください。
