Bagaimana cara memeriksa apakah suatu bilangan adalah bilangan prima dengan Python
Diterbitkan: 2022-05-02Tutorial ini akan mengajarkan Anda cara menulis program Python untuk memeriksa apakah suatu bilangan prima atau tidak.
Jika Anda pernah mengikuti tes pengkodean, Anda akan menemukan pertanyaan matematika pada tes primality atau untuk memeriksa apakah suatu bilangan prima. Dan selama beberapa menit berikutnya, Anda akan belajar menemukan solusi optimal untuk pertanyaan ini.
Dalam tutorial ini, Anda akan:
- mempelajari dasar-dasar bilangan prima,
- tulis kode Python untuk memeriksa apakah suatu bilangan prima, dan
- optimalkan lebih lanjut untuk mendapatkan algoritma runtime O(√n).
Untuk semua ini dan lebih banyak lagi, mari kita mulai.
Apa itu Bilangan Prima?
Mari kita mulai dengan meninjau dasar-dasar bilangan prima.
Dalam teori bilangan, bilangan asli n dikatakan prima jika memiliki tepat dua faktor : 1 dan bilangan itu sendiri ( n ). Ingat dari matematika sekolah Anda: suatu bilangan i dikatakan sebagai faktor dari bilangan n , jika i membagi n secara merata.
Tabel berikut mencantumkan beberapa bilangan, semua faktornya, dan jika bilangan prima.
| n | Faktor | Apakah Perdana? |
| 1 | 1 | Tidak |
| 2 | 1, 2 | Ya |
| 3 | 1, 3 | Ya |
| 4 | 1, 2, 4 | Tidak |
| 7 | 1, 7 | Ya |
| 15 | 1, 3, 5, 15 | Tidak |
Dari tabel di atas dapat kita tuliskan sebagai berikut:
- 2 adalah bilangan prima terkecil.
- 1 adalah faktor dari setiap bilangan.
- Setiap bilangan
nadalah faktor dari dirinya sendiri.
Jadi 1 dan n adalah faktor-faktor sepele untuk setiap nomor n. Dan bilangan prima tidak boleh memiliki faktor selain keduanya.
Ini berarti bahwa ketika Anda beralih dari 2 ke n – 1, Anda seharusnya tidak dapat menemukan faktor non-trivial yang membagi n tanpa sisa.
Algoritma O(n) untuk Memeriksa apakah suatu Angka adalah Prima dengan Python
Di bagian ini, mari kita formalkan pendekatan di atas ke dalam fungsi Python.
Anda dapat mengulang semua angka dari 2 hingga n – 1 menggunakan objek range() dengan Python.
Dalam Python,
range(start, stop, step)mengembalikan objek range. Anda kemudian dapat mengulangi objek rentang untuk mendapatkan urutan daristarthinggastop -1dalam langkahstep.
Karena kita membutuhkan himpunan bilangan bulat dari 2 hingga n-1, kita dapat menentukan range(2, n) dan menggunakannya bersama dengan for loop.
Inilah yang ingin kami lakukan:
- Jika Anda menemukan bilangan yang habis membagi n tanpa sisa, Anda dapat langsung menyimpulkan bahwa bilangan tersebut bukan bilangan prima.
- Jika Anda telah mengulang seluruh barisan bilangan dari 2 hingga n – 1 tanpa menemukan bilangan yang membagi n secara merata, maka bilangan tersebut adalah bilangan prima.
Fungsi Python untuk Memeriksa Bilangan Prima
Dengan menggunakan di atas, kita dapat melanjutkan dan mendefinisikan fungsi is_prime() sebagai berikut.
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return TrueSekarang mari kita urai definisi fungsi di atas.
- Fungsi di atas
is_prime()mengambil bilangan bulat positif n sebagai argumen. - Jika Anda menemukan faktor dalam rentang tertentu (2, n-1), fungsi mengembalikan
False—karena bilangan tersebut bukan bilangan prima. - Dan itu mengembalikan
Truejika Anda melintasi seluruh loop tanpa menemukan faktor.
Selanjutnya, mari kita panggil fungsi dengan argumen dan verifikasi apakah outputnya benar.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True Pada output di atas, Anda melihat bahwa 2 dan 11 adalah bilangan prima (fungsi mengembalikan True ). Dan 8 dan 9 bukan prima (fungsi mengembalikan False ).
Cara Mengoptimalkan Fungsi Python is_prime()
Kita bisa melakukan optimasi kecil-kecilan di sini. Perhatikan daftar faktor pada tabel di bawah ini.
| Nomor | Faktor |
| 6 | 1, 2, 3 , 6 |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
Nah, kita dapat melihat bahwa satu-satunya faktor dari n yang lebih besar dari n/2 adalah n itu sendiri.
Jadi ini berarti Anda tidak perlu mengulang hingga n – 1. Anda dapat menjalankan loop hanya hingga n/2.
Jika Anda tidak menemukan faktor non-sepele hingga n/2, Anda juga tidak dapat menemukan faktor di luar n/2.
Sekarang mari kita ubah fungsi is_prime() untuk memeriksa faktor dalam rentang (2, n/2)
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return TrueMari kita lanjutkan dan verifikasi output melalui beberapa panggilan fungsi.
is_prime(9) # False is_prime(11) # TrueMeskipun sepertinya kami telah mengoptimalkan, algoritme ini tidak lebih efisien daripada yang sebelumnya dalam hal kompleksitas runtime. Faktanya, keduanya memiliki kompleksitas runtime O(n) : sebanding dengan nilai n atau linier dalam n.
Bisakah kita melakukan yang lebih baik? Ya kita bisa!
️ Lanjutkan ke bagian berikutnya untuk menentukan cara meningkatkan kompleksitas waktu untuk pengujian bilangan prima.
Algoritma O(√n) untuk Memeriksa Bilangan Prima dengan Python
Itu terjadi bahwa faktor-faktor suatu bilangan terjadi berpasangan.
Jika a adalah faktor dari bilangan n , maka ada juga faktor b sehingga axb = n , atau sederhananya, ab = n .
Mari kita verifikasi ini melalui sebuah contoh.
Tabel di bawah ini menunjukkan faktor-faktor dari angka 18 yang terjadi secara berpasangan. Anda dapat memverifikasi hal yang sama untuk beberapa nomor lagi jika Anda mau.
Juga, perhatikan bahwa 18 adalah sekitar 4,24.
Dan pada faktor yang terjadi pada pasangan (a, b) , Anda dapat melihat bahwa jika a lebih kecil dari 4,24, maka b lebih besar dari 4,24—dalam contoh ini, (2, 18) dan (3, 6).
| sebuah | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
Gambar di bawah menunjukkan faktor dari 18 yang diplot pada garis bilangan.
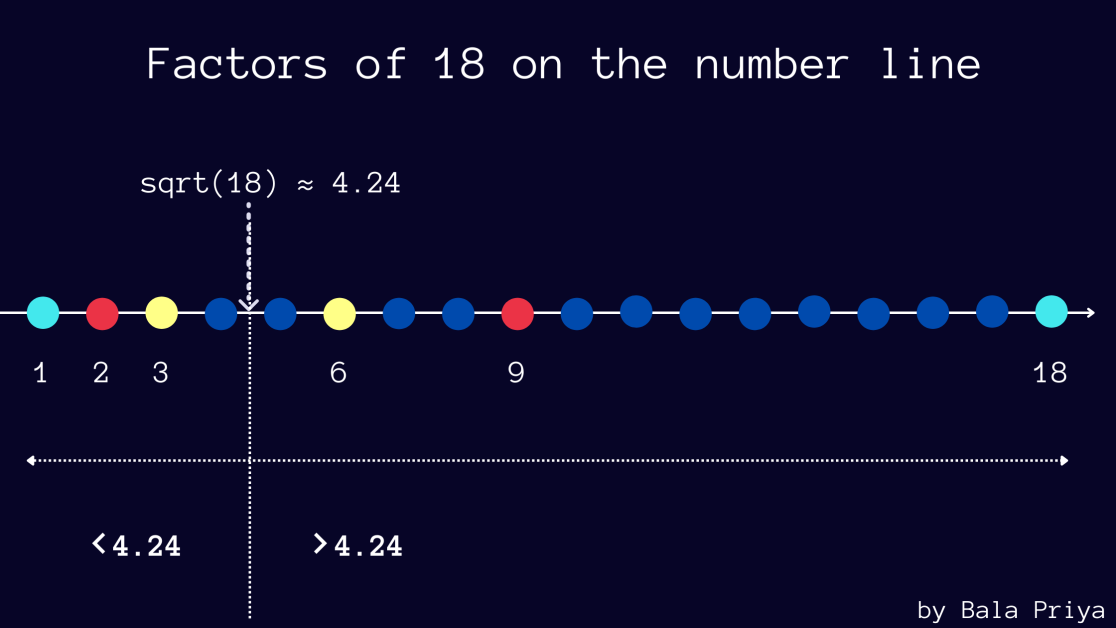
Jika bilangan n merupakan kuadrat sempurna, Anda akan memiliki a = b = n sebagai salah satu faktornya.
️ Perhatikan faktor dari 36 pada tabel di bawah ini. Karena 36 adalah kuadrat sempurna, a = b = 6 adalah salah satu faktornya. Untuk semua pasangan faktor lainnya (a, b), a < 6 dan b > 6 berlaku.
| sebuah | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
Kesimpulannya, kami memiliki yang berikut:
- Setiap bilangan n dapat ditulis sebagai n = axb
- Jika n adalah kuadrat sempurna, maka a = b = n .
- Dan jika a < b , maka, a < n dan b > n .
- Lain, jika a > b , maka a > n dan b < n .
Jadi, alih-alih mengulang semua bilangan bulat hingga n/2, Anda dapat memilih untuk menjalankan hingga n. Dan ini jauh lebih efisien daripada pendekatan kami sebelumnya.
Cara Memodifikasi Algoritma is_prime() ke O(√n)
Mari kita lanjutkan untuk mengoptimalkan fungsi untuk memeriksa bilangan prima dengan Python.
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return TrueSekarang, mari kita urai definisi fungsi di atas:
- Untuk menghitung akar kuadrat dari sebuah angka, mari impor modul matematika bawaan Python, dan gunakan fungsi
math.sqrt(). - Karena n mungkin bukan kuadrat sempurna, kita harus memasukkannya ke dalam bilangan bulat. Gunakan
int(var)untuk memasukkanvarke dalamint. - Untuk memastikan kami benar-benar memeriksa hingga n, kami menambahkan satu plus karena fungsi
range()mengecualikan titik akhir rentang secara default.
Sel kode di bawah ini memverifikasi bahwa fungsi kita is_prime() berfungsi dengan benar.
is_prime(8) # False is_prime(15) # False is_prime(23) # TruePada bagian selanjutnya, mari kita buat beberapa plot sederhana untuk memahami O(n) dan O(√n) secara visual.
Membandingkan O(n) dan O(√n) Secara Visual
️ Jalankan cuplikan kode berikut di lingkungan notebook Jupyter pilihan Anda.
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)Cuplikan di atas menunjukkan bagaimana Anda dapat memplot kurva untuk n dan n untuk rentang nilai.
- Kami menggunakan fungsi NumPy arange() untuk membuat array angka.
- Dan kemudian, kami mengumpulkan nilai n dan n hingga, tetapi tidak termasuk 20, ke dalam panda DataFrame.
- Selanjutnya, kita plot menggunakan fungsi lineplot() seaborn.
Dari plot di bawah, kita melihat bahwa n secara signifikan lebih kecil dari n.
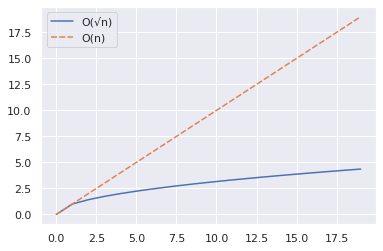
Sekarang mari kita tingkatkan jangkauan hingga 2000 dan ulangi langkah yang sama seperti di atas.
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 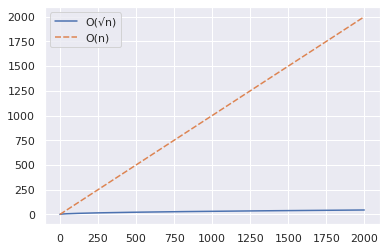
Dari plot di atas, Anda dapat menyimpulkan bahwa algoritma O(√n) secara signifikan lebih cepat saat Anda menguji apakah bilangan prima yang besar.
Berikut ini contoh singkatnya: 2377 adalah bilangan prima—verifikasi ini!
Sementara pendekatan O(n) akan mengambil urutan 2000 langkah, algoritma O(√n) dapat membantu sampai pada jawaban hanya dalam 49 langkah.
Kesimpulan
Dan inilah saatnya untuk ringkasan singkat.
- Untuk memeriksa apakah suatu bilangan prima, pendekatan naif adalah mengulang semua bilangan dalam rentang (2, n-1). Jika Anda tidak menemukan faktor yang membagi n, maka n adalah prima.
- Karena satu-satunya faktor dari n yang lebih besar dari n/2 adalah n itu sendiri, Anda dapat memilih untuk menjalankan hanya hingga n/2.
- Kedua pendekatan di atas memiliki kompleksitas waktu O(n).
- Karena faktor suatu bilangan terjadi berpasangan, Anda hanya dapat menjalankan hingga n. Algoritma ini jauh lebih cepat daripada O(n). Dan keuntungannya cukup besar ketika memeriksa apakah sejumlah besar adalah bilangan prima atau tidak.
Saya harap Anda mengerti cara memeriksa apakah suatu bilangan prima dengan Python. Sebagai langkah selanjutnya, Anda dapat melihat tutorial kami tentang program Python tentang operasi string—di mana Anda akan belajar untuk memeriksa apakah string adalah palindrom, anagram, dan banyak lagi.
Sampai jumpa di tutorial lainnya. Sampai saat itu, selamat coding!

