Jak sprawdzić, czy liczba jest pierwsza w Pythonie?
Opublikowany: 2022-05-02Ten samouczek nauczy Cię, jak napisać program w Pythonie, aby sprawdzić, czy liczba jest liczbą pierwszą, czy nie.
Jeśli kiedykolwiek brałeś udział w testach z kodowania, natknąłeś się na pytanie z matematyki w teście na pierwszorzędność lub sprawdzenie, czy liczba jest pierwsza. W ciągu następnych kilku minut nauczysz się wymyślać optymalne rozwiązanie tego pytania.
W tym samouczku:
- zapoznaj się z podstawami liczb pierwszych,
- napisz kod Pythona, aby sprawdzić, czy liczba jest liczbą pierwszą, i
- zoptymalizuj go dalej, aby uzyskać algorytm czasu pracy O(√n).
Do tego wszystkiego i nie tylko zacznijmy.
Co to jest liczba pierwsza?
Zacznijmy od zapoznania się z podstawami liczb pierwszych.
W teorii liczb o liczbie naturalnej n mówi się, że jest liczbą pierwszą , jeśli ma dokładnie dwa czynniki : 1 i samą liczbę ( n ). Przypomnij sobie ze szkolnej matematyki: mówi się, że liczba i jest czynnikiem liczby n , jeśli i dzieli n równo.
W poniższej tabeli wymieniono kilka liczb, wszystkie ich czynniki oraz liczby pierwsze.
| n | Czynniki | Czy Prime? |
| 1 | 1 | Nie |
| 2 | 1, 2 | TAk |
| 3 | 1, 3 | TAk |
| 4 | 1, 2, 4 | Nie |
| 7 | 1, 7 | TAk |
| 15 | 1, 3, 5, 15 | Nie |
Z powyższej tabeli możemy wypisać:
- 2 to najmniejsza liczba pierwsza.
- 1 to czynnik każdej liczby.
- Każda liczba
njest czynnikiem samym w sobie.
Zatem 1 i n są czynnikami trywialnymi dla dowolnej liczby n. A liczba pierwsza nie powinna mieć żadnych innych czynników niż te dwa.
Oznacza to, że jeśli przejdziesz od 2 do n – 1, nie powinieneś być w stanie znaleźć nietrywialnego czynnika, który dzieli n bez reszty.
Algorytm O(n) sprawdzający, czy liczba jest pierwsza w Pythonie
W tej sekcji sformalizujmy powyższe podejście do funkcji Pythona.
Możesz przejść przez wszystkie liczby od 2 do n – 1 za pomocą obiektu range() w Pythonie.
W Pythonie
range(start, stop, step)zwraca obiekt zakresu. Następnie możesz iterować po obiekcie zakresu, aby uzyskać sekwencję odstartaż dostop -1w krokachstep.
Ponieważ potrzebujemy zestawu liczb całkowitych od 2 do n-1, możemy określić range(2, n) i użyć go w połączeniu z pętlą for .
Oto, co chcielibyśmy zrobić:
- Jeśli znajdziesz liczbę, która dzieli n równo bez reszty, możesz od razu stwierdzić, że liczba ta nie jest liczbą pierwszą.
- Jeśli zapętliłeś cały zakres liczb od 2 aż do n – 1 bez znalezienia liczby, która dzieli n równo, to liczba ta jest liczbą pierwszą.
Funkcja Pythona do sprawdzania liczby pierwszej
Korzystając z powyższego, możemy śmiało zdefiniować funkcję is_prime() w następujący sposób.
def is_prime(n): for i in range(2,n): if (n%i) == 0: return False return TruePrzeanalizujmy teraz powyższą definicję funkcji.
- Powyższa funkcja
is_prime()przyjmuje dodatnią liczbę całkowitą n jako argument. - Jeśli znajdziesz czynnik w określonym zakresie (2, n-1), funkcja zwróci
False— ponieważ liczba nie jest liczbą pierwszą. - I zwraca
True, jeśli przejdziesz całą pętlę bez znalezienia czynnika.
Następnie wywołajmy funkcję z argumentami i sprawdźmy, czy dane wyjściowe są poprawne.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True W powyższym wyniku widać, że 2 i 11 są liczbami pierwszymi (funkcja zwraca True ). A 8 i 9 nie są liczbami pierwszymi (funkcja zwraca False ).
Jak zoptymalizować funkcję Pythona is_prime()
Tutaj możemy zrobić małą optymalizację. Zwróć uwagę na listę czynników w poniższej tabeli.
| Numer | Czynniki |
| 6 | 1, 2, 3 , 6 |
| 10 | 1, 2, 5 , 10 |
| 18 | 1, 2, 3, 6, 9 , 18 |
Cóż, widzimy, że jedynym czynnikiem n , który jest większy niż n/2 , jest samo n .
Oznacza to, że nie musisz zapętlać się aż do n – 1. Zamiast tego możesz uruchomić pętlę tylko do n/2.
Jeśli nie znajdziesz nietrywialnego czynnika do n/2, nie znajdziesz go również poza n/2.
Teraz zmodyfikujmy funkcję is_prime() , aby sprawdzić czynniki z zakresu (2, n/2)
def is_prime(n): for i in range(2,int(n/2)): if (n%i) == 0: return False return TruePrzejdźmy dalej i zweryfikujmy dane wyjściowe za pomocą kilku wywołań funkcji.
is_prime(9) # False is_prime(11) # TrueChociaż może się wydawać, że zoptymalizowaliśmy, ten algorytm nie jest bardziej wydajny niż poprzedni pod względem złożoności środowiska wykonawczego. W rzeczywistości oba mają złożoność czasu wykonania O(n) : proporcjonalną do wartości n lub liniową w n.
Czy możemy zrobić lepiej? Tak możemy!
️ Przejdź do następnej sekcji, aby określić, jak poprawić złożoność czasową testowania liczb pierwszych.
Algorytm O(√n) do sprawdzania liczby pierwszej w Pythonie
Zdarza się, że czynniki liczby występują parami.
Jeśli a jest czynnikiem liczby n , to istnieje również czynnik b taki, że axb = n lub po prostu ab = n .
Zweryfikujmy to na przykładzie.
Poniższa tabela przedstawia współczynniki liczby 18 występujące parami. Możesz zweryfikować to samo dla kilku innych numerów, jeśli chcesz.
Należy również pamiętać, że √18 wynosi około 4,24.
A w czynnikach, które występują w parach (a, b) , widać, że jeśli a jest mniejsze niż 4,24, to b jest większe niż 4,24 — w tym przykładzie (2, 18) i (3,6).
| a | b |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
Poniższy rysunek przedstawia współczynniki 18 wykreślone na osi liczbowej.
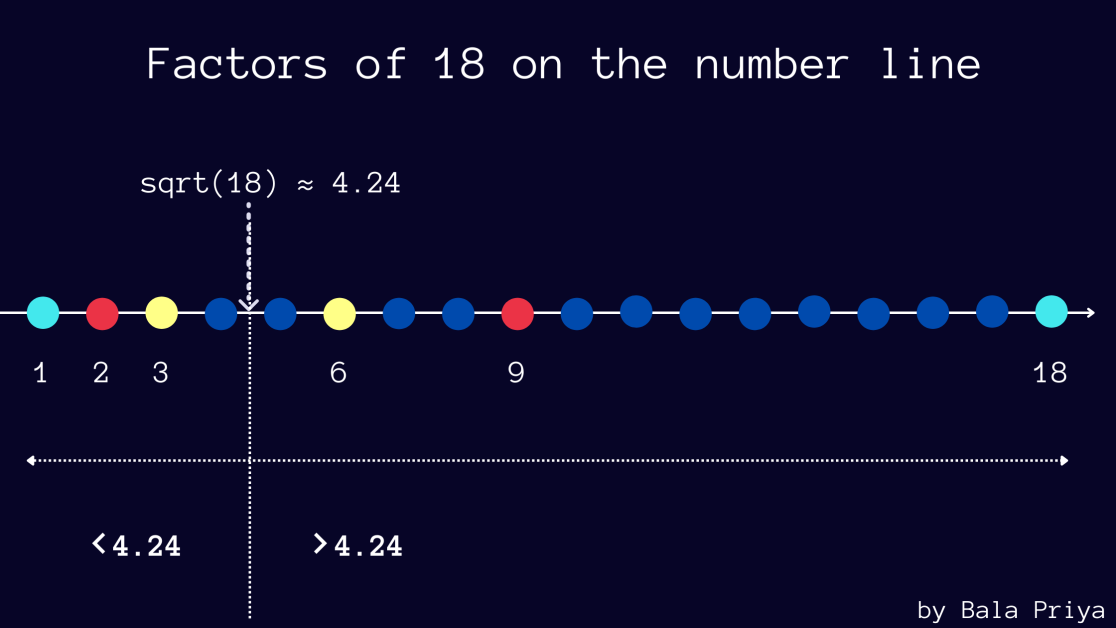
Jeśli liczba n okaże się idealnym kwadratem, będziesz miał a = b = √n jako jeden z czynników.
Spójrz na współczynniki 36 w poniższej tabeli. Ponieważ 36 jest idealnym kwadratem, a = b = 6 jest jednym z czynników. Dla wszystkich pozostałych par czynników (a, b) a < 6 i b > 6 jest spełniony.
| a | b |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
| 6 | 6 |
Podsumowując, mamy następujące:
- Każdą liczbę n można zapisać jako n = axb
- Jeśli n jest idealnym kwadratem, to a = b = √n .
- A jeśli a < b , to a < √n i b > √n .
- W przeciwnym razie, jeśli a > b , to a > √n i b < √n .
Więc zamiast przechodzić przez wszystkie liczby całkowite do n/2, możesz wybrać bieg do √n. A to jest o wiele bardziej wydajne niż nasze poprzednie podejście.
Jak zmienić algorytm is_prime() na O(√n)
Przejdźmy do optymalizacji funkcji, aby sprawdzić liczby pierwsze w Pythonie.
import math def is_prime(n): for i in range(2,int(math.sqrt(n))+1): if (n%i) == 0: return False return TruePrzeanalizujmy teraz powyższą definicję funkcji:
- Aby obliczyć pierwiastek kwadratowy z liczby, zaimportujmy wbudowany moduł matematyczny Pythona i użyjmy funkcji
math.sqrt(). - Ponieważ n może nie być idealnym kwadratem, będziemy musieli zamienić je na liczbę całkowitą. Użyj
int(var), aby rzutowaćvarnaint. - Aby upewnić się, że faktycznie sprawdzamy do √n, dodajemy plus jeden, ponieważ funkcja
range()domyślnie wyklucza punkt końcowy zakresu.
Komórka kodu poniżej weryfikuje, czy nasza funkcja is_prime() działa poprawnie.
is_prime(8) # False is_prime(15) # False is_prime(23) # TrueW następnej sekcji utwórzmy kilka prostych wykresów, aby wizualnie zrozumieć O(n) i O(√n).
Porównanie wizualne O(n) i O(√n)
️ Uruchom następujący fragment kodu w wybranym przez siebie środowisku notesu Jupyter.
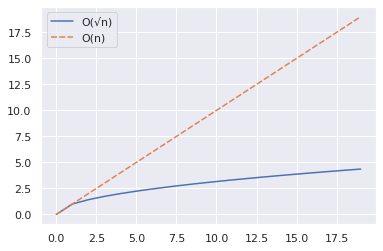
import numpy as np import seaborn as sns import pandas as pd n = 20 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df)Powyższy fragment pokazuje, jak wykreślić krzywe dla n i √n dla zakresu wartości.
- Używamy funkcji NumPy arange(), aby utworzyć tablicę liczb.
- Następnie zbieramy wartości n i √n do, ale nie włączając 20, w pandach DataFrame.
- Następnie wykreślamy za pomocą funkcji lineplot() seaborna.
Z poniższego wykresu widzimy, że √n jest znacznie mniejsze niż n.
Teraz zwiększmy zasięg do 2000 i powtórzmy te same kroki, co powyżej.
import numpy as np import seaborn as sns import pandas as pd n = 2000 x = np.arange(n) y1 = np.sqrt(x) y2 = x df = pd.DataFrame({"O(√n)":y1,"O(n)":y2}) sns.set_theme() sns.lineplot(data = df) 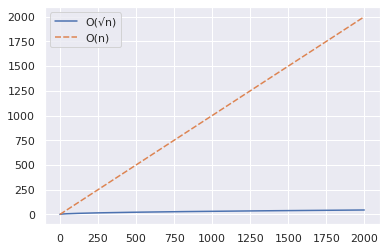
Z powyższego wykresu można wywnioskować, że algorytm O(√n) jest znacznie szybszy, gdy testujesz dużą liczbę jako liczbę pierwszą.
Oto krótki przykład: 2377 to liczba pierwsza — sprawdź to!
Podczas gdy podejście O(n) przyjmie kolejność 2000 kroków, algorytm O(√n) może pomóc w uzyskaniu odpowiedzi w zaledwie 49 krokach.
Wniosek
I czas na szybkie podsumowanie.
- Aby sprawdzić, czy liczba jest liczbą pierwszą, naiwnym podejściem jest przechodzenie przez wszystkie liczby w zakresie (2, n-1). Jeśli nie znajdziesz czynnika, który dzieli n, to n jest liczbą pierwszą.
- Ponieważ jedynym czynnikiem n większym niż n/2 jest samo n, możesz wybrać uruchamianie tylko do n/2.
- Oba powyższe podejścia mają złożoność czasową O(n).
- Ponieważ czynniki liczby występują parami, można uruchomić tylko do √n. Ten algorytm jest dużo szybszy niż O(n). A zysk jest zauważalny podczas sprawdzania, czy duża liczba jest liczbą pierwszą, czy nie.
Mam nadzieję, że rozumiesz, jak sprawdzić, czy liczba jest liczbą pierwszą w Pythonie. W następnym kroku możesz zapoznać się z naszym samouczkiem dotyczącym programów w Pythonie dotyczącym operacji na ciągach — gdzie nauczysz się sprawdzać, czy łańcuchy są palindromami, anagramami i nie tylko.
Do zobaczenia w innym samouczku. Do tego czasu miłego kodowania!

