在 Python 中乘法矩陣的 3 種方法
已發表: 2022-05-09在本教程中,您將學習如何在 Python 中將兩個矩陣相乘。
您將從學習有效矩陣乘法的條件開始,並編寫一個自定義 Python 函數來乘法矩陣。 接下來,您將看到如何使用嵌套列表推導式獲得相同的結果。
最後,您將繼續使用 NumPy 及其內置函數更有效地執行矩陣乘法。
如何檢查矩陣乘法是否有效
在編寫矩陣乘法的 Python 代碼之前,讓我們重溫一下矩陣乘法的基礎知識。
僅當矩陣A中的列數等於矩陣B中的行數時,兩個矩陣 A 和 B 之間的矩陣乘法才有效。
您之前可能遇到過矩陣乘法的這種情況。 然而,你有沒有想過為什麼會這樣?
嗯,這是因為矩陣乘法的工作方式。 看看下面的圖片。
在我們的通用示例中,矩陣 A 有m行和n列。 矩陣 B 有n行p列。

產品矩陣的形狀是什麼?
結果矩陣 C 中索引 (i, j) 處的元素是矩陣 A 的第 i 行和矩陣 B 的第 j 列的點積。
因此,要在結果矩陣 C 中的特定索引處獲取元素,您必須分別計算矩陣 A 和 B 中相應行和列的點積。
重複上述過程,您將得到形狀為mxp的乘積矩陣 C — m行p列,如下所示。

並且兩個向量a和b之間的點積或內積由以下等式給出。

現在總結一下:
- 很明顯,點積僅在相等長度的向量之間定義。
- 因此,要使行和列之間的點積有效——當兩個矩陣相乘時——你需要它們都具有相同數量的元素。
- 在上面的通用示例中,矩陣 A 中的每一行都有n 個元素。 矩陣 B 中的每一列也有n 個元素。
仔細看, n是矩陣A的列數,也是矩陣B的行數。這就是為什麼需要矩陣A的列數等於數的原因矩陣B中的行數。
我希望您了解矩陣乘法有效的條件以及如何獲取乘積矩陣中的每個元素。
讓我們繼續編寫一些 Python 代碼來將兩個矩陣相乘。
編寫一個自定義 Python 函數來乘以矩陣
作為第一步,讓我們編寫一個自定義函數來乘以矩陣。
此功能應執行以下操作:
- 接受兩個矩陣 A 和 B 作為輸入。
- 檢查 A 和 B 之間的矩陣乘法是否有效。
- 如果有效,則將兩個矩陣 A 和 B 相乘,並返回乘積矩陣 C。
- 否則,返回矩陣 A 和 B 不能相乘的錯誤消息。
第 1 步:使用 NumPy 的random.randint()函數生成兩個整數矩陣。 您還可以將矩陣聲明為嵌套的 Python 列表。
import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]] 第 2 步:繼續定義函數multiply_matrix(A,B) 。 此函數將兩個矩陣A和B作為輸入,如果矩陣乘法有效,則返回乘積矩陣C
def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."解析函數定義
讓我們繼續解析函數定義。
將 C 聲明為全局變量:默認情況下,Python 函數內的所有變量都具有局部作用域。 而且您無法從函數外部訪問它們。 為了使乘積矩陣 C 可以從外部訪問,我們必須將其聲明為全局變量。 只需在變量名之前添加global限定符。
檢查矩陣乘法是否有效:使用shape屬性檢查 A 和 B 是否可以相乘。 對於任何數組arr , arr.shape[0]和arr.shape[1]分別給出行數和列數。 因此if A.shape[1] == B.shape[0]檢查矩陣乘法是否有效。 僅當此條件為True時,才會計算乘積矩陣。 否則,該函數將返回錯誤消息。
使用嵌套循環計算值:為了計算結果矩陣的元素,我們必須遍歷矩陣 A 的行,外部for循環執行此操作。 內部for循環幫助我們遍歷矩陣 B 的列。最裡面for循環幫助訪問所選列中的每個元素。
️ 現在我們已經了解了 Python 函數乘以矩陣的工作原理,讓我們用我們之前生成的矩陣 A 和 B 調用該函數。
multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]]) 由於 A 和 B 之間的矩陣乘法有效,因此函數multiply_matrix()返回乘積矩陣 C。
使用 Python 嵌套列表理解將矩陣相乘
在上一節中,您編寫了一個 Python 函數來乘以矩陣。 現在,您將看到如何使用嵌套列表推導來做同樣的事情。
這是乘法矩陣的嵌套列表理解。
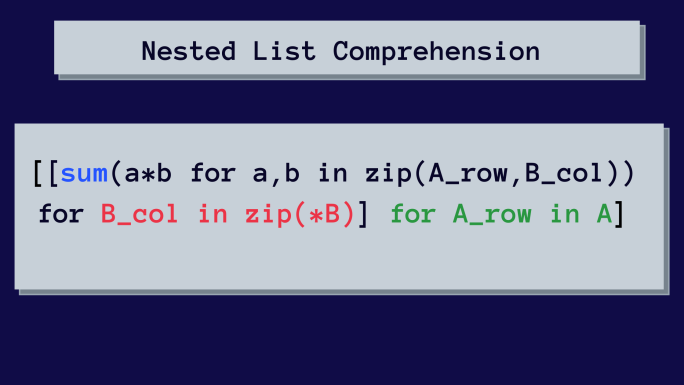
起初,這可能看起來很複雜。 但我們將逐步解析嵌套列表推導。
讓我們一次只關註一個列表理解並確定它的作用。
我們將使用以下通用模板進行列表理解:

[<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through️ 查看我們的指南 List Comprehension in Python – with Examples 以獲得深入的理解。
在繼續之前,請注意,我們希望一次構建結果矩陣 C一行。
嵌套列表理解解釋
第 1 步:計算矩陣 C 中的單個值
給定矩陣 A 的第 i 行和矩陣 B 的第 j 列,下面的表達式給出矩陣 C 中索引 (i, j) 處的條目。
sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on 如果 i = j = 1 ,表達式將返回矩陣 C 的條目c_11 。因此您可以通過這種方式在一行中獲取一個元素。
第 2 步:在矩陣 C 中構建一行
我們的下一個目標是構建一整行。
對於矩陣 A 中的第 1 行,您必須遍歷矩陣 B 中的所有列以在矩陣 C 中獲得完整的一行。
回到列表理解模板。
- 將
<do-this>替換為步驟 1 中的表達式,因為那是您想要做的。 - 接下來,將
<item>替換為B_col— 矩陣 B 中的每一列。 - 最後,將
<iterable>替換為zip(*B)— 包含矩陣 B 中所有列的列表。
這是第一個列表理解。
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B步驟 3:構建所有行並獲得矩陣 C
接下來,您必須通過計算其餘行來填充乘積矩陣 C。
為此,您必須遍歷矩陣 A 中的所有行。
再次返回列表推導,然後執行以下操作。
- 將
<do-this>替換為步驟 2 中的列表推導式。回想一下,我們在上一步中計算了整行。 - 現在,將
<item>替換為A_row矩陣 A 中的每一行。 - 而您的
<iterable>就是矩陣 A 本身,因為您正在遍歷它的行。
這是我們最終的嵌套列表理解。
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]是時候驗證結果了!
# cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]如果你仔細觀察,這相當於我們之前的嵌套 for 循環——只是它更簡潔。
您還可以使用一些內置函數更有效地執行此操作。 讓我們在下一節中了解它們。
在 Python 中使用 NumPy matmul() 對矩陣進行乘法運算
np.matmul()將兩個矩陣作為輸入,如果輸入矩陣之間的矩陣乘法有效,則返回乘積。
C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]] 請注意,此方法比我們之前學習的兩種方法更簡單。 實際上,您可以使用等效的 @ 運算符代替np.matmul() ,我們馬上就會看到。
如何在 Python 中使用 @ 運算符對矩陣進行乘法運算
在 Python 中, @是用於矩陣乘法的二元運算符。
它對兩個矩陣進行運算,通常是 N 維 NumPy 數組,並返回乘積矩陣。
注意:您需要 Python 3.5 及更高版本才能使用
@運算符。
這是您可以使用它的方法。
C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])請注意,乘積矩陣 C 與我們之前獲得的相同。
你可以使用 np.dot() 來乘法矩陣嗎?
如果您曾經遇到過使用np.dot()將兩個矩陣相乘的代碼,那麼它是這樣工作的。
C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]] 您會看到np.dot(A, B)還返回預期的產品矩陣。
但是,根據 NumPy 文檔,您應該只使用np.dot()來計算兩個一維向量的點積,而不是矩陣乘法。
回想一下上一節,乘積矩陣 C 的索引 (i, j) 處的元素是矩陣 A 的第 i 行和矩陣 B 的第 j 列的點積。
由於 NumPy 將此點積運算隱式廣播到所有行和所有列,因此您將得到結果乘積矩陣。 但是為了保持代碼可讀性並避免歧義,請改用np.matmul()或@運算符。
結論
在本教程中,您學習了以下內容。
- 矩陣乘法有效的條件:矩陣A中的列數 = 矩陣B中的行數。
- 如何編寫一個自定義 Python 函數來檢查矩陣乘法是否有效並返回乘積矩陣。 函數體使用嵌套的 for 循環。
- 接下來,您學習瞭如何使用嵌套列表推導來乘以矩陣。 它們比 for 循環更簡潔,但容易出現可讀性問題。
- 最後,您學會了使用 NumPy 內置函數 np.matmul() 來乘法矩陣,以及這在速度方面如何最有效。
- 您還了解了在 Python 中使用@運算符將兩個矩陣相乘。
這結束了我們關於 Python 中的矩陣乘法的討論。 下一步,學習如何在 Python 中檢查一個數字是否為素數。 或者解決有關 Python 字符串的有趣問題。
快樂學習!
