3 modi per moltiplicare le matrici in Python

In questo tutorial imparerai come moltiplicare due matrici in Python.

Inizierai imparando la condizione per una moltiplicazione di matrici valida e scriverai una funzione Python personalizzata per moltiplicare le matrici. Successivamente, vedrai come puoi ottenere lo stesso risultato usando le comprensioni di elenchi nidificati.

Infine, continuerai a utilizzare NumPy e le sue funzioni integrate per eseguire la moltiplicazione di matrici in modo più efficiente.

Come verificare se la moltiplicazione della matrice è valida

Prima di scrivere codice Python per la moltiplicazione di matrici, rivisitiamo le basi della moltiplicazione di matrici.

La moltiplicazione di matrici tra due matrici A e B è valida solo se il numero di colonne nella matrice A è uguale al numero di righe nella matrice B.

Probabilmente ti saresti mai imbattuto in questa condizione per la moltiplicazione di matrici prima. Tuttavia, ti sei mai chiesto perché questo è il caso?

Bene, è a causa del modo in cui funziona la moltiplicazione di matrici. Dai un'occhiata all'immagine qui sotto.

Nel nostro esempio generico, la matrice A ha m righe e n colonne. E la matrice B ha n righe e p colonne.

Qual è la forma della matrice del prodotto?

L'elemento all'indice (i, j) nella matrice risultante C è il prodotto scalare della riga i della matrice A e della colonna j della matrice B.

Quindi, per ottenere un elemento in un particolare indice nella matrice risultante C, dovrai calcolare il prodotto scalare della riga e della colonna corrispondenti nelle matrici A e B, rispettivamente.

Ripetendo il processo sopra, otterrai la matrice prodotto C di forma mxp , con m righe e p colonne, come mostrato di seguito.

E il prodotto scalare o il prodotto interno tra due vettori aeb è dato dalla seguente equazione .

Riassumiamo ora:

• È evidente che il prodotto scalare è definito solo tra vettori di uguale lunghezza.
• Quindi, affinché il prodotto scalare tra una riga e una colonna sia valido, quando si moltiplicano due matrici, è necessario che entrambe abbiano lo stesso numero di elementi.
• Nell'esempio generico sopra, ogni riga della matrice A ha n elementi. E anche ogni colonna della matrice B ha n elementi.

Se osservi più da vicino, n è il numero di colonne nella matrice A, ed è anche il numero di righe nella matrice B. E questo è precisamente il motivo per cui hai bisogno che il numero di colonne nella matrice A sia uguale al numero di righe nella matrice B .

Spero che tu capisca la condizione per la moltiplicazione della matrice per essere valida e come ottenere ogni elemento nella matrice del prodotto.

Procediamo a scrivere del codice Python per moltiplicare due matrici.

Scrivi una funzione Python personalizzata per moltiplicare le matrici

Come primo passo, scriviamo una funzione personalizzata per moltiplicare le matrici.

Questa funzione dovrebbe eseguire le seguenti operazioni:

• Accetta due matrici, A e B, come input.
• Verificare se la moltiplicazione di matrici tra A e B è valida.
• Se valida, moltiplica le due matrici A e B e restituisce la matrice prodotto C.
• Altrimenti, restituisce un messaggio di errore che le matrici A e B non possono essere moltiplicate.

Passaggio 1 : genera due matrici di numeri interi utilizzando la funzione random.randint() di NumPy. Puoi anche dichiarare le matrici come elenchi Python annidati.

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

Passaggio 2: vai avanti e definisci la funzione multiply_matrix(A,B) . Questa funzione accetta due matrici A e B come input e restituisce la matrice prodotto C se la moltiplicazione di matrici è valida.

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

Analisi della definizione della funzione

Procediamo con l'analisi della definizione della funzione.

Dichiara C come variabile globale : per impostazione predefinita, tutte le variabili all'interno di una funzione Python hanno ambito locale . E non puoi accedervi dall'esterno della funzione. Per rendere la matrice prodotto C accessibile dall'esterno, dovremo dichiararla come variabile globale. Basta aggiungere il qualificatore global prima del nome della variabile.

Verificare se la moltiplicazione della matrice è valida: utilizzare l'attributo shape per verificare se A e B possono essere moltiplicati. Per qualsiasi array arr , arr.shape[0] e arr.shape[1] forniscono rispettivamente il numero di righe e colonne . Quindi if A.shape[1] == B.shape[0] verifica se la moltiplicazione di matrici è valida. Solo se questa condizione è True , verrà calcolata la matrice del prodotto. Altrimenti, la funzione restituisce un messaggio di errore.

Usa i cicli annidati per calcolare i valori: per calcolare gli elementi della matrice risultante, dobbiamo scorrere le righe della matrice A e il ciclo for esterno lo fa. Il ciclo for interno ci aiuta a scorrere la colonna della matrice B. E il ciclo for più interno aiuta ad accedere a ciascun elemento nella colonna selezionata.

️ Ora che abbiamo imparato come funziona la funzione Python per moltiplicare le matrici, chiamiamo la funzione con le matrici A e B che abbiamo generato in precedenza.

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

Poiché la moltiplicazione di matrici tra A e B è valida, la funzione multiply_matrix() restituisce la matrice prodotto C.

Usa Python Nested List Comprehension per moltiplicare le matrici

Nella sezione precedente, hai scritto una funzione Python per moltiplicare le matrici. Ora vedrai come puoi utilizzare le comprensioni di elenchi nidificati per fare lo stesso.

Ecco la comprensione dell'elenco annidato per moltiplicare le matrici.

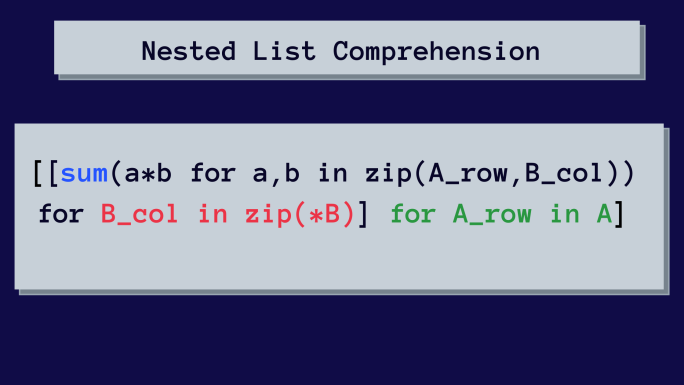
All'inizio, questo può sembrare complicato. Ma analizzeremo passo dopo passo la comprensione dell'elenco annidato.

Concentriamoci sulla comprensione di un elenco alla volta e identifichiamo cosa fa.

Utilizzeremo il seguente modello generale per la comprensione dell'elenco:

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️ Consulta la nostra guida Comprensione dell'elenco in Python - con esempi per ottenere una comprensione approfondita.

Prima di andare avanti, tieni presente che vorremmo costruire la matrice risultante C una riga alla volta.

Spiegazione della comprensione dell'elenco nidificato

Passaggio 1: calcola un singolo valore nella matrice C

Data la riga i della matrice A e la colonna j della matrice B, l'espressione seguente fornisce la voce all'indice (i, j) nella matrice C.

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

Se i = j = 1 , l'espressione restituirà la voce c_11 della matrice C. Quindi puoi ottenere un elemento in una riga in questo modo.

Passaggio 2: costruisci una riga nella matrice C

Il nostro prossimo obiettivo è costruire un'intera fila.

Per la riga 1 nella matrice A, devi scorrere tutte le colonne nella matrice B per ottenere una riga completa nella matrice C.

Torna al modello di comprensione dell'elenco.

• Sostituisci <do-this> con l'espressione del passaggio 1, perché è quello che vuoi fare.
• Quindi, sostituisci <item> con B_col colonna nella matrice B.
• Infine, sostituisci <iterable> con zip(*B) —l'elenco contenente tutte le colonne nella matrice B.

Ed ecco la prima comprensione dell'elenco.

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

Passaggio 3: costruisci tutte le righe e ottieni la matrice C

Successivamente, dovrai popolare la matrice del prodotto C calcolando il resto delle righe.

E per questo, devi scorrere tutte le righe nella matrice A.

Torna alla comprensione dell'elenco ancora una volta e fai quanto segue.

• Sostituisci <do-this> con la comprensione dell'elenco dal passaggio 2. Ricorda che abbiamo calcolato un'intera riga nel passaggio precedente.
• Ora sostituisci <item> con A_row —ogni riga nella matrice A.
• E il tuo <iterable> è la matrice A stessa, mentre stai scorrendo le sue righe.

Ed ecco la nostra ultima comprensione dell'elenco annidato.

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

È ora di verificare il risultato!

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Se dai un'occhiata più da vicino, questo è equivalente ai cicli for nidificati che avevamo in precedenza, solo che è più conciso.

Puoi anche farlo in modo ancora più efficiente usando alcune funzioni integrate. Impariamo a conoscerli nella prossima sezione.

Usa NumPy matmul() per moltiplicare le matrici in Python

Il np.matmul() accetta due matrici come input e restituisce il prodotto se la moltiplicazione di matrici tra le matrici di input è valida .

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Nota come questo metodo sia più semplice dei due metodi che abbiamo imparato in precedenza. In effetti, invece di np.matmul() , puoi usare un operatore @ equivalente e lo vedremo subito.

Come utilizzare @ Operator in Python per moltiplicare le matrici

In Python, @ è un operatore binario utilizzato per la moltiplicazione di matrici.

Opera su due matrici e, in generale, su array NumPy N-dimensionali e restituisce la matrice del prodotto.

Nota: è necessario disporre di Python 3.5 e versioni successive per utilizzare l'operatore @ .

Ecco come puoi usarlo.

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

Si noti che la matrice prodotto C è la stessa che abbiamo ottenuto in precedenza.

Puoi usare np.dot() per moltiplicare le matrici?

Se ti sei mai imbattuto in codice che utilizza np.dot() per moltiplicare due matrici, ecco come funziona.

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Vedrai che np.dot(A, B) restituisce anche la matrice del prodotto previsto.

Tuttavia, come per NumPy docs, dovresti usare np.dot() solo per calcolare il prodotto scalare di due vettori unidimensionali e non per la moltiplicazione di matrici.

Richiamando dalla sezione precedente, l'elemento all'indice (i, j) della matrice prodotto C è il prodotto scalare della riga i della matrice A e della colonna j della matrice B.

Poiché NumPy trasmette implicitamente questa operazione di prodotto punto a tutte le righe e tutte le colonne, ottieni la matrice del prodotto risultante. Ma per mantenere il codice leggibile ed evitare ambiguità, usa np.matmul() o l'operatore @ .

Conclusione

In questo tutorial, hai imparato quanto segue.

• Condizione per la validità della moltiplicazione di matrici: numero di colonne nella matrice A = numero di righe nella matrice B .
• Come scrivere una funzione Python personalizzata che controlla se la moltiplicazione di matrici è valida e restituisce la matrice del prodotto. Il corpo della funzione usa i cicli for nidificati.
• Successivamente, hai imparato come utilizzare le comprensioni di elenchi nidificati per moltiplicare le matrici. Sono più concisi dei cicli for ma sono soggetti a problemi di leggibilità.
• Infine, hai imparato a usare la funzione incorporata di NumPy np.matmul() per moltiplicare le matrici e come questa sia la più efficiente in termini di velocità.
• Hai anche imparato l'operatore @ per moltiplicare due matrici in Python.

E questo conclude la nostra discussione sulla moltiplicazione di matrici in Python. Come passaggio successivo, impara come verificare se un numero è primo in Python. Oppure risolvi problemi interessanti su stringhe Python.

Buon apprendimento!