파이썬에서 행렬을 곱하는 3가지 방법

이 자습서에서는 Python에서 두 행렬을 곱하는 방법을 배웁니다.

유효한 행렬 곱셈에 대한 조건을 학습하고 행렬을 곱하는 사용자 지정 Python 함수를 작성하는 것으로 시작합니다. 다음으로 중첩 목록 이해를 사용하여 동일한 결과를 얻는 방법을 볼 것입니다.

마지막으로 NumPy 및 내장 함수를 사용하여 행렬 곱셈을 보다 효율적으로 수행합니다.

행렬 곱셈이 유효한지 확인하는 방법

행렬 곱셈을 위한 Python 코드를 작성하기 전에 행렬 곱셈의 기본 사항을 다시 살펴보겠습니다.

두 행렬 A 와 B 사이의 행렬 곱셈은 행렬 A 의 열 수가 행렬 B 의 행 개수와 같은 경우에만 유효합니다.

이전에 행렬 곱셈에 대해 이 조건을 접했을 것입니다. 그런데 왜 이런 일이 일어나는지 생각해 본 적이 있습니까?

음, 그것은 행렬 곱셈이 작동하는 방식 때문입니다. 아래 이미지를 살펴보십시오.

일반적인 예에서 행렬 A에는 m 개의 행과 n개의 열이 있습니다. 그리고 행렬 B에는 n개의 행과 p 개의 열이 있습니다.

제품 매트릭스의 모양은 무엇입니까?

결과 행렬 C의 인덱스 (i, j)에 있는 요소는 행렬 A의 행 i와 행렬 B의 열 j의 내적입니다.

따라서 결과 행렬 C의 특정 인덱스에 있는 요소를 얻으려면 행렬 A와 B에 있는 해당 행과 열의 내적을 각각 계산해야 합니다.

위의 과정을 반복하면 아래와 같이 m 개의 행과 p 개의 열이 있는 mxp 모양의 곱 행렬 C를 얻을 수 있습니다.

그리고 두 벡터 a 와 b 사이의 내적 또는 내적은 다음 방정식으로 주어집니다.

이제 요약해 보겠습니다.

• 내적은 길이가 같은 벡터 사이에서만 정의된다는 것이 분명합니다.
• 따라서 행과 열 사이의 내적이 유효하려면(두 행렬을 곱할 때) 두 행렬에 동일한 수의 요소가 있어야 합니다.
• 위의 일반적인 예에서 행렬 A의 모든 행에는 n개의 요소가 있습니다. 그리고 행렬 B의 모든 열에도 n개의 요소가 있습니다.

자세히 살펴보면 n 은 행렬 A의 열 개수이고 행렬 B의 행 개수이기도 합니다. 이것이 바로 행렬 A 의 열 개수가 숫자와 같아야 하는 이유입니다. 행렬 B 의 행 수

행렬 곱셈이 유효한 조건과 곱 행렬의 각 요소를 얻는 방법을 이해하시기 바랍니다.

두 행렬을 곱하는 Python 코드를 작성해 보겠습니다.

행렬을 곱하는 사용자 지정 Python 함수 작성

첫 번째 단계로 행렬을 곱하는 사용자 지정 함수를 작성해 보겠습니다.

이 함수는 다음을 수행해야 합니다.

• 두 개의 행렬 A와 B를 입력값으로 받습니다.
• A와 B 사이의 행렬 곱셈이 유효한지 확인합니다.
• 유효한 경우 두 행렬 A와 B를 곱하고 곱 행렬 C를 반환합니다.
• 그렇지 않으면 행렬 A와 B를 곱할 수 없다는 오류 메시지를 반환합니다.

1단계 : NumPy의 random.randint() 함수를 사용하여 두 개의 정수 행렬을 생성합니다. 행렬을 중첩된 Python 목록으로 선언할 수도 있습니다.

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

2단계: 계속해서 multiply_matrix(A,B) 함수를 정의합니다. 이 함수는 두 개의 행렬 A 와 B 를 입력으로 받아 행렬 곱셈이 유효한 경우 곱 행렬 C 를 반환합니다.

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

함수 정의 구문 분석

함수 정의 구문 분석을 진행해 보겠습니다.

C를 전역 변수로 선언 : 기본적으로 Python 함수 내부의 모든 변수에는 지역 범위 가 있습니다. 그리고 함수 외부에서 접근할 수 없습니다. 제품 행렬 C를 외부에서 액세스할 수 있도록 하려면 전역 변수로 선언해야 합니다. 변수 이름 앞에 global 한정자를 추가하기만 하면 됩니다.

행렬 곱셈이 유효한지 확인: shape 속성을 사용하여 A와 B를 곱할 수 있는지 확인합니다. 모든 배열에 대해 arr , arr.shape[0] 및 arr.shape[1] 은 각각 행 과 열의 수를 제공합니다. 따라서 if A.shape[1] == B.shape[0] 이면 행렬 곱셈이 유효한지 확인합니다. 이 조건이 True 인 경우에만 제품 행렬이 계산됩니다. 그렇지 않으면 함수는 오류 메시지를 반환합니다.

중첩 루프를 사용하여 값 계산: 결과 행렬의 요소를 계산하려면 행렬 A의 행을 반복해야 하며 외부 for 루프가 이 작업을 수행합니다. 내부 for 루프는 행렬 B의 열을 순환하는 데 도움이 됩니다. 그리고 가장 안쪽에 있는 for 루프는 선택한 열의 각 요소에 액세스하는 데 도움이 됩니다.

️ 이제 행렬을 곱하는 Python 함수가 작동하는 방식을 배웠으므로 이전에 생성한 행렬 A와 B를 사용하여 함수를 호출해 보겠습니다.

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

A와 B 사이의 행렬 곱셈이 유효하기 때문에 multiply_matrix() 함수는 곱 행렬 C를 반환합니다.

Python 중첩 목록 이해를 사용하여 행렬 곱하기

이전 섹션에서 행렬을 곱하는 Python 함수를 작성했습니다. 이제 중첩 목록 이해를 사용하여 동일한 작업을 수행하는 방법을 볼 수 있습니다.

다음은 행렬을 곱하기 위한 중첩 목록 이해입니다.

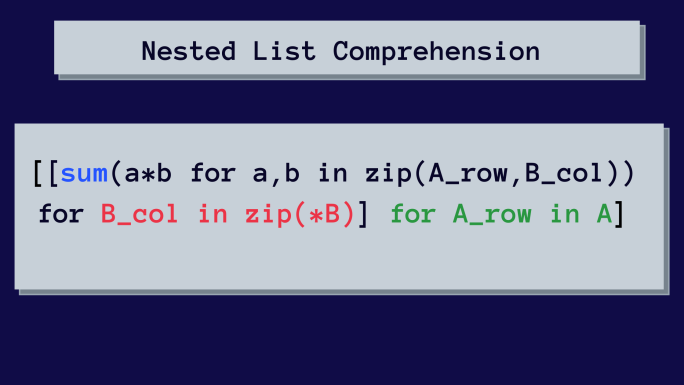
처음에는 이것이 복잡해 보일 수 있습니다. 그러나 우리는 중첩 목록 이해를 단계별로 구문 분석할 것입니다.

한 번에 하나의 목록 이해에 집중하고 그것이 하는 일을 식별해 봅시다.

목록 이해를 위해 다음 일반 템플릿을 사용합니다.

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️ 심층적인 이해를 얻으려면 예제가 포함된 Python의 목록 이해 가이드를 확인하세요.

계속 진행하기 전에 결과 행렬 C를 한 번에 한 행씩 작성하고 싶습니다.

중첩 목록 이해 설명

1단계: 행렬 C에서 단일 값 계산

행렬 A의 행 i와 행렬 B의 열 j가 주어지면 아래 식은 행렬 C의 인덱스 (i, j)에 있는 항목을 제공합니다.

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

만약에 i = j = 1 , 표현식은 행렬 C의 항목 c_11 을 반환합니다. 따라서 이 방법으로 한 행에서 하나의 요소를 얻을 수 있습니다.

2단계: 행렬 C에서 하나의 행 만들기

다음 목표는 전체 행을 만드는 것입니다.

행렬 A의 행 1에 대해 행렬 C의 완전한 행 하나를 얻으려면 행렬 B의 모든 열을 반복해야 합니다.

목록 이해 템플릿으로 돌아갑니다.

• <do-this> 를 1단계의 표현식으로 바꾸십시오. 이것이 바로 여러분이 원하는 것이기 때문입니다.
• 다음으로, <item> 을 B_col —행렬 B의 각 열로 바꿉니다.
• 마지막으로 <iterable> 을 행렬 B의 모든 열을 포함하는 목록인 zip(*B) 으로 바꿉니다.

다음은 첫 번째 목록 이해입니다.

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

3단계: 모든 행을 만들고 행렬 C를 얻습니다.

다음으로 나머지 행을 계산하여 곱 행렬 C를 채워야 합니다.

그리고 이를 위해서는 행렬 A의 모든 행을 반복해야 합니다.

다시 목록 이해로 돌아가서 다음을 수행하십시오.

• <do-this> 를 2단계의 목록 이해로 대체하십시오. 이전 단계에서 전체 행을 계산했음을 기억하십시오.
• 이제 <item> 을 A_row —행렬 A의 모든 행으로 바꾸십시오.
• 그리고 <iterable> 은 행을 반복하면서 행렬 A 자체입니다.

다음은 최종 중첩 목록 이해입니다.

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

결과를 확인할 시간입니다!

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

자세히 살펴보면 이전에 사용했던 중첩 for 루프와 동일하며 더 간결합니다.

또한 일부 내장 함수를 사용하여 더욱 효율적으로 이 작업을 수행할 수 있습니다. 다음 섹션에서 이에 대해 알아보겠습니다.

NumPy matmul()을 사용하여 Python에서 행렬 곱하기

np.matmul() 은 두 개의 행렬을 입력으로 사용하고 입력 행렬 간의 행렬 곱셈이 유효한 경우 곱을 반환합니다.

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

이 방법이 이전에 배운 두 가지 방법보다 더 간단합니다. 사실, np.matmul() 대신에 동등한 @ 연산자를 사용할 수 있으며, 우리는 그것을 바로 보게 될 것입니다.

행렬을 곱하기 위해 Python에서 @ 연산자를 사용하는 방법

Python에서 @ 는 행렬 곱셈에 사용되는 이항 연산자입니다.

두 개의 행렬, 일반적으로 N차원 NumPy 배열에서 작동하고 곱 행렬을 반환합니다.

참고: @ 연산자를 사용하려면 Python 3.5 이상이 필요합니다.

사용 방법은 다음과 같습니다.

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

곱 행렬 C는 이전에 얻은 것과 동일합니다.

np.dot()를 사용하여 행렬을 곱할 수 있습니까?

np.dot() 를 사용하여 두 행렬을 곱하는 코드를 본 적이 있다면 다음과 같이 작동합니다.

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

np.dot(A, B) 도 예상 곱 행렬을 반환한다는 것을 알 수 있습니다.

그러나 NumPy 문서에 np.dot() 는 행렬 곱셈이 아니라 2개의 1차원 벡터의 내적을 계산할 때만 사용해야 합니다.

이전 섹션에서, 곱 행렬 C의 인덱스 (i, j)에 있는 요소는 행렬 A의 행 i와 행렬 B의 열 j의 내적입니다.

NumPy는 이 내적 연산을 모든 행과 모든 열에 암시적으로 브로드캐스트하므로 결과 곱 행렬을 얻습니다. 그러나 코드를 읽기 쉽게 유지하고 모호성을 피하려면 대신 np.matmul() 또는 @ 연산자를 사용하십시오.

결론

이 자습서에서는 다음을 배웠습니다.

• 행렬 곱셈이 유효하기 위한 조건: 행렬 A 의 열 개수 = 행렬 B 의 행 개수.
• 행렬 곱셈이 유효한지 확인하고 곱 행렬을 반환하는 사용자 지정 Python 함수를 작성하는 방법. 함수의 본문은 중첩 for 루프를 사용합니다.
• 다음으로 중첩 목록 이해를 사용하여 행렬을 곱하는 방법을 배웠습니다. for 루프보다 간결하지만 가독성 문제가 발생하기 쉽습니다.
• 마지막으로 NumPy 내장 함수 np.matmul()을 사용하여 행렬을 곱하는 방법과 이것이 속도 면에서 가장 효율적인 방법을 배웠습니다.
• 또한 Python에서 두 행렬을 곱하는 @ 연산자에 대해서도 배웠습니다.

이것으로 파이썬의 행렬 곱셈에 대한 논의를 마치겠습니다. 다음 단계로 파이썬에서 숫자가 소수인지 확인하는 방법을 배웁니다. 또는 Python 문자열에 대한 흥미로운 문제를 해결하십시오.

즐거운 배움!