3 طرق لمضاعفة المصفوفات في بايثون

في هذا البرنامج التعليمي ، ستتعلم كيفية ضرب مصفوفتين في بايثون.

ستبدأ بتعلم شرط مضاعفة المصفوفة الصحيحة وكتابة دالة بايثون مخصصة لمضاعفة المصفوفات. بعد ذلك ، سترى كيف يمكنك تحقيق نفس النتيجة باستخدام قوائم شاملة متداخلة.

أخيرًا ، ستنتقل إلى استخدام NumPy ووظائفه المضمنة لإجراء مضاعفة المصفوفة بشكل أكثر كفاءة.

كيفية التحقق من صحة المصفوفة

قبل كتابة كود Python لضرب المصفوفة ، دعنا نعيد النظر في أساسيات ضرب المصفوفة.

يعد ضرب المصفوفة بين مصفوفتين A و B صالحًا فقط إذا كان عدد الأعمدة في المصفوفة A يساوي عدد الصفوف في المصفوفة B.

من المحتمل أن تكون قد صادفت هذا الشرط الخاص بضرب المصفوفة من قبل. ومع ذلك ، هل تساءلت يومًا عن سبب حدوث ذلك؟

حسنًا ، هذا بسبب طريقة عمل ضرب المصفوفات. ألق نظرة على الصورة أدناه.

في مثالنا العام ، تحتوي المصفوفة A على صفوف m و n من الأعمدة. والمصفوفة B بها n من الصفوف والأعمدة p .

ما هو شكل مصفوفة المنتج؟

العنصر في الفهرس (i، j) في المصفوفة الناتجة C هو حاصل الضرب القياسي للصف i من المصفوفة A والعمود j من المصفوفة B.

لذلك للحصول على عنصر في فهرس معين في المصفوفة الناتجة C ، يجب عليك حساب حاصل الضرب القياسي للصف والعمود المقابل في المصفوفتين A و B ، على التوالي.

بتكرار العملية أعلاه ، ستحصل على مصفوفة المنتج C للشكل mxp - مع m من الصفوف والأعمدة p ، كما هو موضح أدناه.

وحاصل الضرب القياسي أو الناتج الداخلي بين متجهين أ و ب معطى بالمعادلة التالية.

دعونا نلخص الآن:

• من الواضح أن حاصل الضرب النقطي محدد فقط بين متجهات متساوية الطول.
• لذا ، لكي يكون حاصل الضرب النقطي بين صف وعمود صالحًا - عند ضرب مصفوفتين - يجب أن يكون لكل منهما نفس عدد العناصر.
• في المثال العام أعلاه ، يحتوي كل صف في المصفوفة A على عدد n من العناصر. ويحتوي كل عمود في المصفوفة B على عدد n من العناصر أيضًا.

إذا ألقيت نظرة فاحصة ، فإن n هو عدد الأعمدة في المصفوفة A ، وهو أيضًا عدد الصفوف في المصفوفة B. وهذا هو بالضبط سبب احتياجك لعدد الأعمدة في المصفوفة A ليكون مساويًا للعدد من الصفوف في المصفوفة ب .

أتمنى أن تفهم شرط أن يكون ضرب المصفوفة صحيحًا وكيفية الحصول على كل عنصر في مصفوفة المنتج.

دعنا ننتقل إلى كتابة بعض كود Python لضرب مصفوفتين.

اكتب دالة بايثون مخصصة لمضاعفة المصفوفات

كخطوة أولى ، دعنا نكتب دالة مخصصة لضرب المصفوفات.

يجب أن تقوم هذه الوظيفة بما يلي:

• اقبل مصفوفتين ، A و B ، كمدخلات.
• تحقق مما إذا كان ضرب المصفوفة بين A و B صحيحًا.
• إذا كان ذلك صحيحًا ، فاضرب المصفوفتين A و B ، وأعد مصفوفة حاصل الضرب C.
• عدا ذلك ، قم بإرجاع رسالة خطأ مفادها أنه لا يمكن مضاعفة المصفوفتين A و B.

الخطوة 1 : أنشئ مصفوفتين من الأعداد الصحيحة باستخدام random.randint() في NumPy. يمكنك أيضًا إعلان المصفوفات كقوائم بايثون المتداخلة.

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

الخطوة 2: انطلق وحدد الدالة multiply_matrix(A,B) . تأخذ هذه الدالة مصفوفتين A و B كمدخلات وتعيد مصفوفة المنتج C إذا كان ضرب المصفوفة صالحًا.

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

تحليل تعريف الوظيفة

دعنا ننتقل إلى تحليل تعريف الوظيفة.

قم بتعريف C كمتغير عالمي : بشكل افتراضي ، جميع المتغيرات داخل دالة Python لها نطاق محلي . ولا يمكنك الوصول إليها من خارج الوظيفة. لجعل مصفوفة حاصل الضرب C قابلة للوصول من الخارج ، علينا أن نعلن أنها متغير عالمي. فقط أضف global العام قبل اسم المتغير.

تحقق مما إذا كان ضرب المصفوفة صحيحًا: استخدم سمة shape للتحقق مما إذا كان يمكن ضرب A و B. لأية مصفوفة arr arr.shape[0] و arr.shape[1] أعط عدد الصفوف والأعمدة ، على التوالي. لذلك if A.shape[1] == B.shape[0] إذا كان ضرب المصفوفة صحيحًا. فقط إذا كان هذا الشرط True ، فسيتم حساب مصفوفة المنتج. عدا ذلك ، تقوم الوظيفة بإرجاع رسالة خطأ.

استخدم الحلقات المتداخلة لحساب القيم: لحساب عناصر المصفوفة الناتجة ، علينا أن نمر عبر صفوف المصفوفة A ، وتقوم حلقة for الخارجية بهذا. تساعدنا حلقة for الداخلية على الالتفاف عبر عمود المصفوفة B. وتساعد حلقة for الداخلية في الوصول إلى كل عنصر في العمود المحدد.

️ الآن بعد أن تعلمنا كيف تعمل دالة Python لضرب المصفوفات ، فلنسمي الدالة بالمصفوفتين A و B اللتين أنشأناهما سابقًا.

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

نظرًا لأن ضرب المصفوفة بين A و B صالح ، فإن الدالة multiply_matrix() تُرجع مصفوفة المنتج C.

استخدم قائمة Python المتداخلة لمضاعفة المصفوفات

في القسم السابق ، كتبت دالة بايثون لمضاعفة المصفوفات. الآن ، سترى كيف يمكنك استخدام قوائم شاملة متداخلة لفعل الشيء نفسه.

إليك قائمة شاملة متداخلة لضرب المصفوفات.

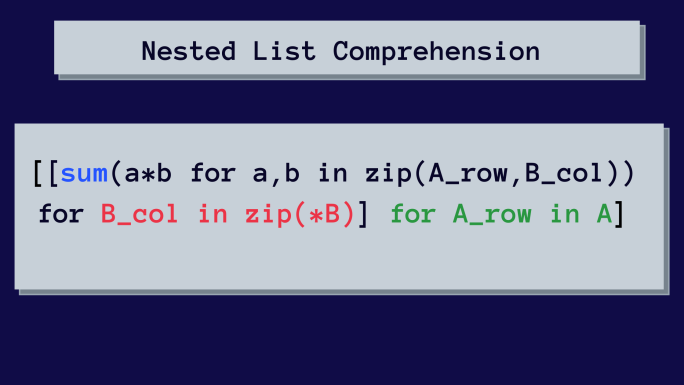
في البداية ، قد يبدو هذا معقدًا. لكننا سنحلل قائمة الفهم المتداخلة خطوة بخطوة.

دعونا نركز على فهم قائمة واحدة في كل مرة ونحدد ما يفعله.

سنستخدم النموذج العام التالي لفهم القائمة:

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️ تحقق من دليلنا لفهم القائمة في Python - مع أمثلة للحصول على فهم متعمق.

قبل المضي قدمًا ، يرجى ملاحظة أننا نرغب في بناء المصفوفة الناتجة C صفًا واحدًا في كل مرة.

شرح قائمة متداخلة

الخطوة 1: احسب قيمة وحيدة في المصفوفة ج

بالنظر إلى الصف i من المصفوفة A والعمود j من المصفوفة B ، فإن التعبير أدناه يعطي الإدخال في الفهرس (i، j) في المصفوفة C.

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

إذا i = j = 1 ، سيعود التعبير الإدخال c_11 من المصفوفة C. لذا يمكنك الحصول على عنصر واحد في صف واحد بهذه الطريقة.

الخطوة 2: بناء صف واحد في المصفوفة ج

هدفنا التالي هو بناء صف كامل.

بالنسبة للصف 1 في المصفوفة A ، عليك أن تمر عبر جميع الأعمدة في المصفوفة B للحصول على صف واحد كامل في المصفوفة C.

ارجع إلى نموذج قائمة الفهم.

• استبدل <do-this> بالتعبير من الخطوة 1 ، لأن هذا ما تريد القيام به.
• بعد ذلك ، استبدل <item> بـ B_col عمود في المصفوفة B.
• أخيرًا ، <iterable> بـ zip(*B) —القائمة التي تحتوي على جميع الأعمدة في المصفوفة B.

وهنا أول قائمة الفهم.

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

الخطوة 3: قم ببناء كل الصفوف والحصول على المصفوفة ج

بعد ذلك ، سيتعين عليك ملء مصفوفة المنتج C بحساب بقية الصفوف.

ولهذا ، عليك تكرار كل صفوف المصفوفة أ.

عد إلى قائمة الفهم مرة أخرى ، وقم بما يلي.

• استبدل <do-this> بقائمة الفهم من الخطوة 2. تذكر أننا قمنا بحساب صف كامل في الخطوة السابقة.
• الآن ، استبدل <item> بـ A_row كل صف في المصفوفة أ.
• و <iterable> هو المصفوفة A نفسها ، حيث تقوم بالتكرار عبر صفوفها.

وإليك قائمة الفهم النهائية المتداخلة.

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

حان الوقت للتحقق من النتيجة!

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

إذا ألقيت نظرة فاحصة ، فهذا يعادل حلقات for المتداخلة التي كانت لدينا سابقًا - إنها أكثر إيجازًا.

يمكنك أيضًا القيام بذلك بشكل أكثر كفاءة باستخدام بعض الوظائف المضمنة. دعنا نتعرف عليها في القسم التالي.

استخدم NumPy matmul () لمضاعفة المصفوفات في Python

يأخذ np.matmul() مصفوفتين كمدخلات ويعيد المنتج إذا كان ضرب المصفوفة بين مصفوفات الإدخال صحيحًا .

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

لاحظ كيف أن هذه الطريقة أبسط من الطريقتين اللتين تعلمناه سابقًا. في الواقع ، بدلاً من np.matmul() ، يمكنك استخدام معامل @ مكافئ ، وسنرى ذلك على الفور.

كيفية استخدام @ Operator في Python لمضاعفة المصفوفات

في Python ، @ هو عامل ثنائي يستخدم لضرب المصفوفة.

وهي تعمل على مصفوفتين ، وبشكل عام ، مصفوفات NumPy ذات الأبعاد N ، وتعيد مصفوفة المنتج.

ملاحظة: يجب أن يكون لديك Python 3.5 والإصدارات الأحدث لاستخدام عامل التشغيل @ .

إليك كيف يمكنك استخدامه.

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

لاحظ أن مصفوفة حاصل الضرب C هي نفسها التي حصلنا عليها سابقًا.

هل يمكنك استخدام np.dot () لمضاعفة المصفوفات؟

إذا صادفت يومًا رمزًا يستخدم np.dot() لضرب مصفوفتين ، فإليك طريقة عمله.

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

سترى أن np.dot(A, B) تُرجع أيضًا مصفوفة المنتج المتوقعة.

ومع ذلك ، وفقًا لمستندات NumPy ، يجب عليك استخدام np.dot() فقط لحساب حاصل الضرب النقطي لمتجهين أحادي البعد وليس ضرب المصفوفة.

تذكر من القسم السابق ، أن العنصر في الفهرس (i، j) من مصفوفة الضرب C هو حاصل الضرب القياسي للصف i من المصفوفة A ، والعمود j من المصفوفة B.

نظرًا لأن NumPy يبث ضمنيًا عملية المنتج النقطي هذه إلى جميع الصفوف وجميع الأعمدة ، فإنك تحصل على مصفوفة المنتج الناتجة. ولكن للحفاظ على الكود الخاص بك قابلاً للقراءة وتجنب الغموض ، استخدم np.matmul() أو عامل التشغيل @ بدلاً من ذلك.

استنتاج

في هذا البرنامج التعليمي ، تعلمت ما يلي.

• شرط أن يكون ضرب المصفوفة صحيحًا: عدد الأعمدة في المصفوفة A = عدد الصفوف في المصفوفة B.
• كيفية كتابة دالة Python مخصصة للتحقق مما إذا كان ضرب المصفوفة صالحًا وإرجاع مصفوفة المنتج. يستخدم جسم الوظيفة حلقات for المتداخلة.
• بعد ذلك ، تعلمت كيفية استخدام القوائم المتداخلة لضرب المصفوفات. إنها أكثر إيجازًا من حلقات for ولكنها عرضة لمشاكل القراءة.
• أخيرًا ، تعلمت استخدام دالة NumPy المضمنة np.matmul () لمضاعفة المصفوفات وكيف أن هذا هو الأكثر كفاءة من حيث السرعة.
• لقد تعرفت أيضًا على عامل التشغيل @ لمضاعفة مصفوفتين في Python.

وهذا يختتم مناقشتنا حول ضرب المصفوفات في بايثون. كخطوة تالية ، تعرف على كيفية التحقق مما إذا كان الرقم أوليًا في بايثون. أو حل مشاكل مثيرة للاهتمام في سلاسل Python.

تعلم سعيد!