3 Cara Mengalikan Matriks dengan Python

Dalam tutorial ini, Anda akan belajar cara mengalikan dua matriks dengan Python.

Anda akan mulai dengan mempelajari kondisi perkalian matriks yang valid dan menulis fungsi Python khusus untuk mengalikan matriks. Selanjutnya, Anda akan melihat bagaimana Anda dapat mencapai hasil yang sama menggunakan pemahaman daftar bersarang.

Terakhir, Anda akan melanjutkan menggunakan NumPy dan fungsi bawaannya untuk melakukan perkalian matriks dengan lebih efisien.

Cara Memeriksa apakah Perkalian Matriks Valid

Sebelum menulis kode Python untuk perkalian matriks, mari kita tinjau kembali dasar-dasar perkalian matriks.

Perkalian Matriks antara dua matriks A dan B hanya valid jika jumlah kolom pada matriks A sama dengan jumlah baris pada matriks B .

Anda mungkin pernah menemukan kondisi ini untuk perkalian matriks sebelumnya. Namun, pernahkah Anda bertanya-tanya mengapa hal ini terjadi?

Yah, itu karena cara kerja perkalian matriks. Lihatlah gambar di bawah ini.

Dalam contoh umum kami, matriks A memiliki m baris dan n kolom. Dan matriks B memiliki n baris dan p kolom.

Apa Bentuk Matriks Produk?

Elemen pada indeks (i,j) dalam matriks resultan C adalah hasil kali titik dari baris i matriks A, dan kolom j dari matriks B.

Jadi untuk mendapatkan elemen pada indeks tertentu dalam matriks C yang dihasilkan, Anda harus menghitung produk titik dari baris dan kolom yang sesuai dalam matriks A dan B, masing-masing.

Mengulangi proses di atas, Anda akan mendapatkan matriks produk C berbentuk mxp —dengan m baris dan p kolom, seperti yang ditunjukkan di bawah ini.

Dan hasil kali titik atau hasil kali dalam antara dua vektor a dan b diberikan oleh persamaan berikut.

Mari kita rangkum sekarang:

• Terbukti bahwa hasil kali titik hanya didefinisikan antara vektor-vektor yang sama panjang.
• Jadi agar perkalian titik antara baris dan kolom valid—saat mengalikan dua matriks—Anda memerlukan keduanya memiliki jumlah elemen yang sama.
• Dalam contoh umum di atas, setiap baris dalam matriks A memiliki n elemen. Dan setiap kolom dalam matriks B juga memiliki n elemen.

Jika Anda melihat lebih dekat, n adalah jumlah kolom dalam matriks A, dan juga jumlah baris dalam matriks B. Dan inilah alasan mengapa Anda membutuhkan jumlah kolom dalam matriks A sama dengan jumlah baris dalam matriks B .

Saya harap Anda memahami kondisi perkalian matriks menjadi valid dan bagaimana mendapatkan setiap elemen dalam matriks produk.

Mari kita lanjutkan menulis beberapa kode Python untuk mengalikan dua matriks.

Tulis Fungsi Python Kustom untuk Mengalikan Matriks

Sebagai langkah pertama, mari kita menulis fungsi kustom untuk mengalikan matriks.

Fungsi ini harus melakukan hal berikut:

• Terima dua matriks, A dan B, sebagai input.
• Periksa apakah perkalian matriks antara A dan B valid.
• Jika valid, kalikan dua matriks A dan B, dan kembalikan matriks hasil kali C.
• Jika tidak, kembalikan pesan kesalahan bahwa matriks A dan B tidak dapat dikalikan.

Langkah 1 : Buat dua matriks bilangan bulat menggunakan fungsi random.randint() NumPy. Anda juga dapat mendeklarasikan matriks sebagai daftar Python bersarang.

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

Langkah 2: Lanjutkan dan definisikan fungsi multiply_matrix(A,B) . Fungsi ini mengambil dua matriks A dan B sebagai input dan mengembalikan matriks produk C jika perkalian matriks valid.

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

Mengurai Definisi Fungsi

Mari kita lanjutkan untuk mengurai definisi fungsi.

Deklarasikan C sebagai variabel global : Secara default, semua variabel di dalam fungsi Python memiliki lingkup lokal . Dan Anda tidak dapat mengaksesnya dari luar fungsi. Untuk membuat matriks produk C dapat diakses dari luar, kita harus mendeklarasikannya sebagai variabel global. Cukup tambahkan qualifier global sebelum nama variabel.

Periksa apakah perkalian matriks valid: Gunakan atribut shape untuk memeriksa apakah A dan B dapat dikalikan. Untuk sembarang array arr , arr.shape[0] dan arr.shape[1] masing-masing memberikan jumlah baris dan kolom . Jadi if A.shape[1] == B.shape[0] memeriksa apakah perkalian matriks valid. Hanya jika kondisi ini True , matriks produk akan dihitung. Jika tidak, fungsi mengembalikan pesan kesalahan.

Gunakan loop bersarang untuk menghitung nilai: Untuk menghitung elemen matriks yang dihasilkan, kita harus mengulang baris matriks A, dan loop for luar melakukan ini. Perulangan for bagian dalam membantu kita mengulang melalui kolom matriks B. Dan perulangan for terdalam membantu mengakses setiap elemen dalam kolom yang dipilih.

️ Sekarang setelah kita mempelajari cara kerja fungsi Python untuk mengalikan matriks, mari kita panggil fungsi dengan matriks A dan B yang kita buat sebelumnya.

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

Karena perkalian matriks antara A dan B valid, fungsi multiply_matrix() mengembalikan matriks produk C.

Gunakan Pemahaman Daftar Bersarang Python untuk Mengalikan Matriks

Di bagian sebelumnya, Anda menulis fungsi Python untuk mengalikan matriks. Sekarang, Anda akan melihat bagaimana Anda dapat menggunakan pemahaman daftar bersarang untuk melakukan hal yang sama.

Berikut pemahaman daftar bersarang untuk mengalikan matriks.

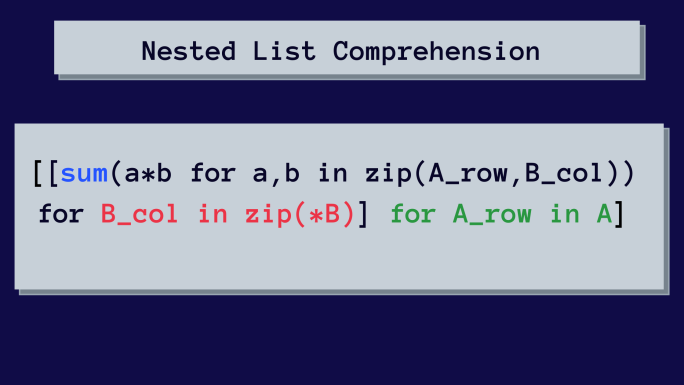
Pada awalnya, ini mungkin terlihat rumit. Tapi kami akan menguraikan pemahaman daftar bersarang langkah demi langkah.

Mari kita fokus pada satu pemahaman daftar pada satu waktu dan mengidentifikasi apa yang dilakukannya.

Kami akan menggunakan template umum berikut untuk pemahaman daftar:

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️ Lihat panduan Daftar Pemahaman kami dengan Python – dengan Contoh untuk mendapatkan pemahaman yang mendalam.

Sebelum melanjutkan, harap perhatikan bahwa kami ingin membangun matriks C yang dihasilkan satu baris pada satu waktu.

Pemahaman Daftar Bersarang Dijelaskan

Langkah 1: Hitung satu nilai dalam matriks C

Diberikan baris i dari matriks A dan kolom j dari matriks B, ekspresi di bawah ini memberikan entri pada indeks (i, j) dalam matriks C.

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

Jika i = j = 1 , ekspresi akan mengembalikan entri c_11 dari matriks C. Jadi Anda bisa mendapatkan satu elemen dalam satu baris dengan cara ini.

Langkah 2: Bangun satu baris dalam matriks C

Tujuan kami selanjutnya adalah membangun seluruh baris.

Untuk baris 1 dalam matriks A, Anda harus mengulang semua kolom dalam matriks B untuk mendapatkan satu baris lengkap dalam matriks C.

Kembali ke templat pemahaman daftar.

• Ganti <do-this> dengan ekspresi dari langkah 1, karena itulah yang ingin Anda lakukan.
• Selanjutnya, ganti <item> dengan B_col kolom dalam matriks B.
• Terakhir, ganti <iterable> dengan zip(*B) —daftar yang berisi semua kolom dalam matriks B.

Dan inilah daftar pemahaman pertama.

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

Langkah 3: Bangun semua baris dan dapatkan matriks C

Selanjutnya, Anda harus mengisi matriks produk C dengan menghitung sisa baris.

Dan untuk ini, Anda harus mengulang semua baris dalam matriks A.

Kembali ke pemahaman daftar lagi, dan lakukan hal berikut.

• Ganti <do-this> dengan pemahaman daftar dari langkah 2. Ingat bahwa kita menghitung seluruh baris pada langkah sebelumnya.
• Sekarang, ganti <item> dengan A_row baris dalam matriks A.
• Dan <iterable> Anda adalah matriks A itu sendiri, saat Anda mengulang barisnya.

Dan inilah pemahaman daftar bersarang terakhir kami.

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

Saatnya untuk memverifikasi hasilnya!

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Jika Anda melihat lebih dekat, ini setara dengan perulangan for bersarang yang kita miliki sebelumnya—hanya saja lebih ringkas.

Anda juga dapat melakukan ini dengan lebih efisien menggunakan beberapa fungsi bawaan. Mari kita pelajari tentang mereka di bagian selanjutnya.

Gunakan NumPy matmul() untuk Mengalikan Matriks dengan Python

np.matmul() mengambil dua matriks sebagai input dan mengembalikan produk jika perkalian matriks antara matriks input valid .

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Perhatikan bagaimana metode ini lebih sederhana daripada dua metode yang kita pelajari sebelumnya. Faktanya, alih-alih np.matmul() , Anda dapat menggunakan operator @ yang setara, dan kita akan segera melihatnya.

Cara Menggunakan @ Operator dengan Python untuk Mengalikan Matriks

Dalam Python, @ adalah operator biner yang digunakan untuk perkalian matriks.

Ini beroperasi pada dua matriks, dan secara umum, array NumPy N-dimensi, dan mengembalikan matriks produk.

Catatan: Anda harus memiliki Python 3.5 dan yang lebih baru untuk menggunakan operator @ .

Inilah cara Anda dapat menggunakannya.

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

Perhatikan bahwa matriks produk C sama dengan yang kita peroleh sebelumnya.

Bisakah Anda Menggunakan np.dot() untuk Mengalikan Matriks?

Jika Anda pernah menemukan kode yang menggunakan np.dot() untuk mengalikan dua matriks, berikut cara kerjanya.

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Anda akan melihat bahwa np.dot(A, B) juga mengembalikan matriks produk yang diharapkan.

Namun, sesuai dengan NumPy docs, Anda harus menggunakan np.dot() hanya untuk menghitung produk titik dari dua vektor satu dimensi dan bukan untuk perkalian matriks.

Ingat kembali dari bagian sebelumnya, elemen pada indeks (i, j) dari matriks produk C adalah produk titik dari baris i matriks A, dan kolom j matriks B.

Karena NumPy secara implisit menyiarkan operasi produk titik ini ke semua baris dan semua kolom, Anda mendapatkan matriks produk yang dihasilkan. Tetapi agar kode Anda dapat dibaca dan menghindari ambiguitas, gunakan np.matmul() atau operator @ sebagai gantinya.

Kesimpulan

Dalam tutorial ini, Anda telah mempelajari hal berikut.

• Syarat perkalian matriks valid: jumlah kolom pada matriks A = jumlah baris pada matriks B .
• Cara menulis fungsi Python khusus yang memeriksa apakah perkalian matriks valid dan mengembalikan matriks produk. Tubuh fungsi menggunakan loop for bersarang.
• Selanjutnya, Anda mempelajari cara menggunakan pemahaman daftar bersarang untuk mengalikan matriks. Mereka lebih ringkas daripada untuk loop tetapi rentan terhadap masalah keterbacaan.
• Terakhir, Anda belajar menggunakan fungsi bawaan NumPy np.matmul() untuk mengalikan matriks dan cara ini paling efisien dalam hal kecepatan.
• Anda juga belajar tentang operator @ untuk mengalikan dua matriks dengan Python.

Dan itu mengakhiri diskusi kita tentang perkalian matriks dengan Python. Sebagai langkah selanjutnya, pelajari cara memeriksa apakah suatu bilangan prima dengan Python. Atau pecahkan masalah menarik pada string Python.

Selamat belajar!