Pythonで行列を乗算する3つの方法

このチュートリアルでは、Pythonで2つの行列を乗算する方法を学習します。

まず、有効な行列乗算の条件を学習し、行列を乗算するカスタムPython関数を記述します。 次に、ネストされたリスト内包表記を使用して同じ結果を達成する方法を確認します。

最後に、NumPyとその組み込み関数を使用して、行列の乗算をより効率的に実行します。

行列の乗算が有効かどうかを確認する方法

行列乗算用のPythonコードを作成する前に、行列乗算の基本を再確認しましょう。

2つの行列AとBの間の行列の乗算は、行列Aの列の数が行列Bの行の数と等しい場合にのみ有効です。

以前は、行列の乗算でこの条件に遭遇したことがあるでしょう。 しかし、なぜこれが当てはまるのか疑問に思ったことはありますか？

まあ、それは行列の乗算が機能する方法のためです。 下の画像を見てください。

一般的な例では、行列Aにはm行n列があります。 また、行列Bにはn行p列があります。

製品マトリックスの形状は何ですか？

結果の行列Cのインデックス（i、j）の要素は、行列Aの行iと行列Bの列jの内積です。

したがって、結果の行列Cの特定のインデックスで要素を取得するには、それぞれ行列AとBの対応する行と列の内積を計算する必要があります。

上記のプロセスを繰り返すと、以下に示すように、 m行p列の形状mxpの積行列Cが得られます。

また、2つのベクトルaとbの間の内積または内積は、次の式で与えられます。

ここで要約しましょう：

• 内積が同じ長さのベクトル間でのみ定義されていることは明らかです。
• したがって、行と列の間の内積が有効であるためには（2つの行列を乗算する場合）、両方が同じ数の要素を持つ必要があります。
• 上記の一般的な例では、行列Aのすべての行にn個の要素があります。 また、行列Bのすべての列にもn個の要素があります。

よく見ると、 nは行列Aの列数であり、行列Bの行数でもあります。これが、行列Aの列数を数と等しくする必要がある理由です。行列Bの行の数。

行列の乗算が有効であるための条件と、積行列の各要素を取得する方法を理解していただければ幸いです。

2つの行列を乗算するPythonコードの記述に進みましょう。

行列を乗算するカスタムPython関数を作成する

最初のステップとして、行列を乗算するカスタム関数を作成しましょう。

この関数は次のことを行う必要があります。

• 2つの行列AとBを入力として受け入れます。
• AとBの間の行列の乗算が有効かどうかを確認してください。
• 有効な場合は、2つの行列AとBを乗算し、積行列Cを返します。
• それ以外の場合は、行列AとBを乗算できないというエラーメッセージを返します。

ステップ1 ： NumPyのrandom.randint()関数を使用して整数の2つの行列を生成します。 行列をネストされたPythonリストとして宣言することもできます。

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

ステップ2：先に進み、関数multiply_matrix(A,B)を定義します。 この関数は、2つの行列AとBを入力として受け取り、行列の乗算が有効な場合は積行列Cを返します。

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

関数定義の解析

関数定義の解析に進みましょう。

Cをグローバル変数として宣言する：デフォルトでは、Python関数内のすべての変数はローカルスコープを持っています。 また、関数の外部からそれらにアクセスすることはできません。 製品行列Cに外部からアクセスできるようにするには、それをグローバル変数として宣言する必要があります。 変数名の前にglobal修飾子を追加するだけです。

行列の乗算が有効かどうかを確認しますshape属性を使用して、AとBを乗算できるかどうかを確認します。 任意の配列arrについて、 arr.shape[0]とarr.shape[1]は、それぞれ行と列の数を示します。 したがってif A.shape[1] == B.shape[0]の場合、行列の乗算が有効かどうかがチェックされます。 この条件がTrueの場合にのみ、積行列が計算されます。 それ以外の場合、関数はエラーメッセージを返します。

ネストされたループを使用して値を計算します。結果の行列の要素を計算するには、行列Aの行をループする必要があり、外側forループがこれを行います。 内側forループは、行列Bの列をループするのに役立ちます。また、最も内側forループは、選択した列の各要素にアクセスするのに役立ちます。

️行列を乗算するPython関数がどのように機能するかを学習したので、前に生成した行列AとBを使用して関数を呼び出しましょう。

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

AとBの間の行列の乗算が有効であるため、関数multiply_matrix()は積行列Cを返します。

Pythonネストリスト内包表記を使用して行列を乗算する

前のセクションでは、行列を乗算するPython関数を作成しました。 これで、ネストされたリスト内包表記を使用して同じことを行う方法がわかります。

これが、行列を乗算するためのネストされたリスト内包表記です。

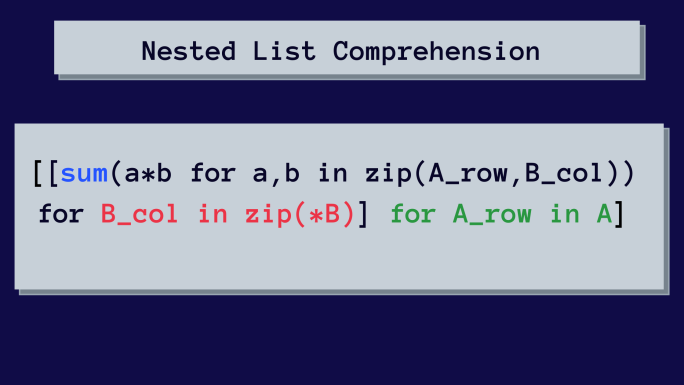
最初は、これは複雑に見えるかもしれません。 ただし、ネストされたリスト内包表記を段階的に解析します。

一度に1つのリスト内包に焦点を合わせ、それが何をするかを特定しましょう。

リスト内包表記には、次の一般的なテンプレートを使用します。

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️Pythonでのリスト内包表記のガイドを確認してください–詳細な理解を得るための例を示します。

先に進む前に、結果の行列Cを一度に1行ずつ作成したいことに注意してください。

ネストされたリスト内包表記の説明

ステップ1：行列Cの単一の値を計算します

行列Aの行iと行列Bの列jが与えられると、次の式は行列Cのインデックス（i、j）にエントリを与えます。

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

もしも i = j = 1の場合、式は行列Cのエントリc_11を返します。したがって、この方法で1つの行に1つの要素を取得できます。

ステップ2：行列Cに1つの行を作成します

次の目標は、行全体を作成することです。

行列Aの行1の場合、行列Bのすべての列をループして、行列Cの1つの完全な行を取得する必要があります。

リスト内包表記テンプレートに戻ります。

• <do-this>をステップ1の式に置き換えます。これが、実行したいことだからです。
• 次に、 <item>をB_colに置き換えます—行列Bの各列。
• 最後に、 <iterable>をzip(*B) （行列Bのすべての列を含むリスト）に置き換えます。

そして、これが最初のリスト内包表記です。

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

ステップ3：すべての行を作成し、行列Cを取得します

次に、残りの行を計算して、積行列Cを入力する必要があります。

このためには、行列Aのすべての行をループする必要があります。

もう一度リスト内包に戻り、次の手順を実行します。

• <do-this>をステップ2のリスト内包に置き換えます。前のステップで行全体を計算したことを思い出してください。
• ここで、 <item>をA_rowに置き換えます—行列Aのすべての行。
• そして、あなたの<iterable>は、その行をループしているので、行列A自体です。

そして、これが最後のネストされたリスト内包表記です。

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

結果を確認する時が来ました！

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

よく見ると、これは以前にネストされたforループと同等ですが、より簡潔になっています。

また、いくつかの組み込み関数を使用して、これをさらに効率的に行うことができます。 次のセクションでそれらについて学びましょう。

NumPy matmul（）を使用してPythonで行列を乗算する

np.matmul()は、入力として2つの行列を受け取り、入力行列間の行列の乗算が有効な場合は積を返します。

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

この方法が、以前に学習した2つの方法よりも単純であることに注意してください。 実際、 np.matmul()の代わりに、同等の@演算子を使用できます。これは、すぐにわかります。

Pythonで@演算子を使用して行列を乗算する方法

Pythonでは、 @は行列の乗算に使用される二項演算子です。

これは、2つの行列、および一般にN次元のNumPy配列で動作し、積行列を返します。

注： @演算子を使用するには、Python3.5以降が必要です。

使い方は次のとおりです。

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

積行列Cは、前に取得したものと同じであることに注意してください。

np.dot（）を使用して行列を乗算できますか？

np.dot()を使用して2つの行列を乗算するコードに出くわしたことがある場合は、次のように機能します。

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

np.dot(A, B)も期待される積行列を返すことがわかります。

ただし、NumPyのドキュメントによると、 np.dot()は、行列の乗算ではなく、2つの1次元ベクトルの内積を計算するためにのみ使用する必要があります。

前のセクションを思い出してください。積行列Cのインデックス（i、j）の要素は、行列Aの行iと行列Bの列jの内積です。

NumPyがこのドット積演算をすべての行とすべての列に暗黙的にブロードキャストすると、結果の積行列が得られます。 ただし、コードを読みやすくし、あいまいさを避けるために、代わりにnp.matmul()または@演算子を使用してください。

結論

このチュートリアルでは、次のことを学びました。

• 行列の乗算が有効であるための条件：行列Aの列数=行列Bの行数。
• 行列の乗算が有効かどうかをチェックし、積行列を返すカスタムPython関数を作成する方法。 関数の本体は、ネストされたforループを使用します。
• 次に、ネストされたリスト内包表記を使用して行列を乗算する方法を学習しました。 forループよりも簡潔ですが、読みやすさの問題が発生しやすくなります。
• 最後に、NumPyの組み込み関数np.matmul（）を使用して行列を乗算する方法と、これが速度の点で最も効率的である方法を学びました。
• また、Pythonで2つの行列を乗算する@演算子についても学びました。

これで、Pythonでの行列の乗算に関する説明は終わりです。 次のステップとして、Pythonで数値が素数であるかどうかを確認する方法を学びます。 または、Python文字列に関する興味深い問題を解決します。

幸せな学習！