Python'da Matrisleri Çarpmanın 3 Yolu

Bu öğreticide, Python'da iki matrisin nasıl çarpılacağını öğreneceksiniz.

Geçerli matris çarpma koşulunu öğrenerek başlayacak ve matrisleri çarpmak için özel bir Python işlevi yazacaksınız. Ardından, iç içe liste kavrayışlarını kullanarak aynı sonucu nasıl elde edebileceğinizi göreceksiniz.

Son olarak, matris çarpımını daha verimli bir şekilde gerçekleştirmek için NumPy ve yerleşik işlevlerini kullanmaya devam edeceksiniz.

Matris Çarpımının Geçerli Olup Olmadığı Nasıl Kontrol Edilir

Matris çarpımı için Python kodunu yazmadan önce, matris çarpımının temellerini tekrar gözden geçirelim.

A ve B matrisleri arasındaki matris çarpımı, yalnızca A matrisindeki sütunların sayısı B matrisindeki satırların sayısına eşitse geçerlidir.

Matris çarpımı için bu koşulla muhtemelen daha önce karşılaşmışsınızdır. Ancak, bunun neden böyle olduğunu hiç merak ettiniz mi?

Şey, bunun nedeni matris çarpımının çalışma şekli. Aşağıdaki resme bir göz atın.

Genel örneğimizde, A matrisinin m satırı ve n sütunu vardır. Ve B matrisinin n satırı ve p sütunu var.

Ürün Matrisinin Şekli Nedir?

Elde edilen C matrisindeki (i, j) indeksindeki eleman, A matrisinin i satırının ve B matrisinin j sütununun nokta çarpımıdır.

Bu nedenle, sonuçtaki C matrisinde belirli bir dizinde bir öğe elde etmek için, sırasıyla A ve B matrislerinde karşılık gelen satır ve sütunun nokta çarpımını hesaplamanız gerekir.

Yukarıdaki işlemi tekrarlayarak, aşağıda gösterildiği gibi m satır ve p sütunlu mxp şeklindeki C çarpım matrisini elde edeceksiniz.

Ve iki a ve b vektörü arasındaki nokta çarpım veya iç çarpım aşağıdaki denklemle verilir.

Şimdi özetleyelim:

• Nokta çarpımının yalnızca eşit uzunluktaki vektörler arasında tanımlandığı açıktır.
• Bu nedenle, bir satır ve bir sütun arasındaki nokta çarpımının geçerli olması için - iki matrisi çarparken - her ikisinin de aynı sayıda öğeye sahip olması gerekir.
• Yukarıdaki genel örnekte, A matrisindeki her satırda n eleman vardır. Ve B matrisindeki her sütunda da n eleman var.

Daha yakından bakarsanız, n , A matrisindeki sütunların sayısıdır ve aynı zamanda B matrisindeki satırların sayısıdır. Ve bu, tam olarak, A matrisindeki sütun sayısının sayıya eşit olmasına ihtiyaç duymanızın nedenidir. B matrisindeki satır sayısı .

Umarım matris çarpımının geçerli olma koşulunu ve çarpım matrisindeki her bir elemanın nasıl elde edileceğini anlamışsınızdır.

İki matrisi çarpmak için bir Python kodu yazmaya devam edelim.

Matrisleri Çarpmak İçin Özel Bir Python İşlevi Yazın

İlk adım olarak, matrisleri çarpmak için özel bir fonksiyon yazalım.

Bu işlev aşağıdakileri yapmalıdır:

• A ve B olmak üzere iki matrisi girdi olarak kabul edin.
• A ve B arasındaki matris çarpımının geçerli olup olmadığını kontrol edin.
• Geçerliyse, A ve B matrislerini çarpın ve C çarpım matrisini döndürün.
• Aksi takdirde, A ve B matrislerinin çarpılamayacağına dair bir hata mesajı döndürün.

Adım 1 : NumPy'nin random.randint() işlevini kullanarak iki tam sayı matrisi oluşturun. Ayrıca matrisleri iç içe Python listeleri olarak da bildirebilirsiniz.

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

Adım 2: Devam edin ve multiply_matrix(A,B) işlevini tanımlayın. Bu işlev A ve B matrislerini girdi olarak alır ve matris çarpımı geçerliyse C çarpım matrisini döndürür.

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

İşlev Tanımını Ayrıştırma

Fonksiyon tanımını ayrıştırmaya devam edelim.

C'yi global bir değişken olarak bildirin : Varsayılan olarak, bir Python işlevi içindeki tüm değişkenlerin yerel kapsamı vardır. Ve onlara fonksiyonun dışından erişemezsiniz. C çarpım matrisini dışarıdan erişilebilir kılmak için, onu global bir değişken olarak tanımlamamız gerekecek. Değişken adından önce global niteleyiciyi eklemeniz yeterlidir.

Matris çarpımının geçerli olup olmadığını kontrol edin: A ve B'nin çarpılıp çarpılmadığını kontrol etmek için shape özniteliğini kullanın. Herhangi bir arr dizisi için arr.shape[0] ve arr.shape[1] sırasıyla satır ve sütun sayısını verir. Yani if A.shape[1] == B.shape[0] matris çarpımının geçerli olup olmadığını kontrol eder. Yalnızca bu koşul True ise çarpım matrisi hesaplanır. Aksi takdirde, işlev bir hata mesajı döndürür.

Değerleri hesaplamak için iç içe döngüler kullanın: Elde edilen matrisin öğelerini hesaplamak için, A matrisinin satırları arasında döngü yapmalıyız ve dış for döngüsü bunu yapar. İçteki for döngüsü, B matrisinin sütununda döngü yapmamıza yardımcı olur. Ve en içteki for döngüsü, seçilen sütundaki her öğeye erişmemize yardımcı olur.

️ Artık matrisleri çarpmak için Python fonksiyonunun nasıl çalıştığını öğrendiğimize göre, daha önce oluşturduğumuz A ve B matrisleriyle fonksiyonu çağıralım.

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

A ve B arasındaki matris çarpımı geçerli olduğundan, multiply_matrix() işlevi, C çarpım matrisini döndürür.

Matrisleri Çarpmak için Python İç İçe Liste Anlayışını Kullanın

Önceki bölümde matrisleri çarpmak için bir Python işlevi yazdınız. Şimdi, aynı şeyi yapmak için iç içe liste anlamalarını nasıl kullanabileceğinizi göreceksiniz.

İşte matrisleri çarpmak için iç içe liste anlayışı.

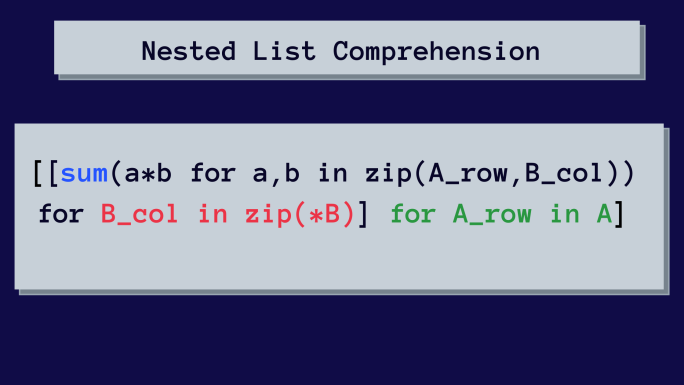
İlk başta, bu karmaşık görünebilir. Ancak iç içe liste kavrayışını adım adım ayrıştıracağız.

Her seferinde bir liste kavrayışına odaklanalım ve ne yaptığını belirleyelim.

Listeyi anlamak için aşağıdaki genel şablonu kullanacağız:

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️ Derinlemesine bir anlayış kazanmak için Örneklerle Python'da Liste Anlama kılavuzumuza göz atın.

Devam etmeden önce, elde edilen C matrisini her seferinde bir satır oluşturmak istediğimizi lütfen unutmayın.

İç İçe Liste Anlama Açıklaması

Adım 1: C matrisinde tek bir değer hesaplayın

A matrisinin i satırı ve B matrisinin j sütunu verildiğinde, aşağıdaki ifade C matrisindeki (i, j) indeksindeki girişi verir.

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

Eğer i = j = 1 , ifade C matrisinin c_11 girişini döndürür. Böylece bu şekilde bir satırda bir eleman elde edebilirsiniz.

Adım 2: C matrisinde bir satır oluşturun

Bir sonraki hedefimiz bütün bir sıra oluşturmak.

A matrisindeki 1. satır için, C matrisinde bir tam satır elde etmek için B matrisindeki tüm sütunlar arasında dolaşmanız gerekir.

Liste anlama şablonuna geri dönün.

• <do-this> adım 1'deki ifadeyle değiştirin, çünkü yapmak istediğiniz bu.
• Ardından, <item> B_col — B matrisindeki her sütunla değiştirin.
• Son olarak, <iterable> zip(*B) ile değiştirin—B matrisindeki tüm sütunları içeren liste.

Ve işte ilk liste kavrayışı.

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

Adım 3: Tüm satırları oluşturun ve C matrisini elde edin

Ardından, satırların geri kalanını hesaplayarak C çarpım matrisini doldurmanız gerekecek.

Ve bunun için, A matrisindeki tüm satırlar arasında dolaşmanız gerekir.

Liste kavrayışına tekrar dönün ve aşağıdakileri yapın.

• <do-this> adım 2'deki liste kavrayışı ile değiştirin. Önceki adımda bir satırın tamamını hesapladığımızı hatırlayın.
• Şimdi, <item> A_row ile değiştirin; A matrisindeki her satır.
• Ve <iterable> değeriniz, siz onun satırları arasında dolaşırken A matrisinin kendisidir.

Ve işte son iç içe liste anlayışımız.

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

Sonucu doğrulamanın zamanı geldi!

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Daha yakından bakarsanız, bu daha önce sahip olduğumuz iç içe for döngülerine eşdeğerdir - sadece daha özlü.

Ayrıca bazı yerleşik işlevleri kullanarak bunu daha verimli bir şekilde yapabilirsiniz. Bir sonraki bölümde onlar hakkında bilgi edinelim.

Python'da Matrisleri Çarpmak için NumPy matmul() kullanın

np.matmul() girdi olarak iki matris alır ve girdi matrisleri arasındaki matris çarpımı geçerliyse ürünü döndürür.

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Bu yöntemin daha önce öğrendiğimiz iki yöntemden nasıl daha basit olduğuna dikkat edin. Aslında, np.matmul() yerine eşdeğer bir @ operatörü kullanabilirsiniz ve bunu hemen göreceğiz.

Matrisleri Çarpmak için Python'da @ Operator Nasıl Kullanılır

Python'da @ , matris çarpımı için kullanılan ikili bir operatördür.

İki matris ve genel olarak N-boyutlu NumPy dizileri üzerinde çalışır ve çarpım matrisini döndürür.

Not: @ operatörünü kullanmak için Python 3.5 ve sonraki bir sürüme sahip olmanız gerekir.

Bunu nasıl kullanabileceğiniz aşağıda açıklanmıştır.

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

C çarpım matrisinin daha önce elde ettiğimizle aynı olduğuna dikkat edin.

Matrisleri Çarpmak için np.dot() Kullanabilir misiniz?

İki matrisi çarpmak için np.dot() kullanan bir kodla karşılaştıysanız, işte nasıl çalıştığı.

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

np.dot(A, B) de beklenen çarpım matrisini döndürdüğünü göreceksiniz.

Ancak, NumPy belgelerine göre, matris çarpımı için değil, yalnızca iki tek boyutlu vektörün nokta çarpımını hesaplamak için np.dot() kullanmalısınız.

Önceki bölümden hatırlayın, C çarpım matrisinin (i, j) indeksindeki eleman, A matrisinin i satırının ve B matrisinin j sütununun nokta çarpımıdır.

NumPy bu nokta çarpım işlemini tüm satırlara ve tüm sütunlara örtük olarak yayınladığından, sonuçtaki çarpım matrisini alırsınız. Ancak kodunuzu okunabilir kılmak ve belirsizliği önlemek için bunun yerine np.matmul() veya @ operatörünü kullanın.

Çözüm

Bu eğitimde, aşağıdakileri öğrendiniz.

• Matris çarpımının geçerli olması için koşul: A matrisindeki sütun sayısı = B matrisindeki satır sayısı.
• Matris çarpımının geçerli olup olmadığını kontrol eden ve çarpım matrisini döndüren özel bir Python işlevi nasıl yazılır. Fonksiyonun gövdesi iç içe for döngülerini kullanır.
• Ardından, matrisleri çarpmak için iç içe liste kavrayışlarını nasıl kullanacağınızı öğrendiniz. Döngüler için olduğundan daha özlüdürler ancak okunabilirlik sorunlarına eğilimlidirler.
• Son olarak, matrisleri çarpmak için NumPy yerleşik işlevi np.matmul()'u kullanmayı ve bunun hız açısından nasıl en verimli olduğunu öğrendiniz.
• Python'da iki matrisi çarpmak için @ operatörünü de öğrendiniz.

Bu da Python'da matris çarpımı konusundaki tartışmamızı tamamlıyor. Bir sonraki adım olarak, Python'da bir sayının asal olup olmadığını nasıl kontrol edeceğinizi öğrenin. Veya Python dizilerindeki ilginç problemleri çözün.

Mutlu öğrenme!