3 способа умножения матриц в Python

В этом уроке вы узнаете, как перемножить две матрицы в Python.

Вы начнете с изучения условия допустимого умножения матриц и напишете пользовательскую функцию Python для умножения матриц. Далее вы увидите, как можно добиться того же результата, используя вложенные генераторы списков.

Наконец, вы приступите к использованию NumPy и его встроенных функций для более эффективного выполнения матричного умножения.

Как проверить правильность умножения матриц

Прежде чем писать код Python для умножения матриц, давайте вернемся к основам умножения матриц.

Умножение матриц между двумя матрицами A и B допустимо только в том случае, если количество столбцов в матрице A равно количеству строк в матрице B .

Вероятно, вы уже встречались с этим условием умножения матриц раньше. Однако задумывались ли вы когда-нибудь, почему это так?

Ну, это из-за того, как работает умножение матриц. Взгляните на изображение ниже.

В нашем общем примере матрица A имеет m строк и n столбцов. А матрица B имеет n строк и p столбцов.

Какова форма матрицы продуктов?

Элемент с индексом (i, j) в результирующей матрице C является скалярным произведением строки i матрицы A и столбца j матрицы B.

Таким образом, чтобы получить элемент с определенным индексом в результирующей матрице C, вам придется вычислить скалярное произведение соответствующей строки и столбца в матрицах A и B соответственно.

Повторяя описанный выше процесс, вы получите матрицу произведения C формы mxp — с m строк и p столбцов, как показано ниже.

А скалярный продукт или внутренний продукт между двумя векторами a и b задается следующим уравнением.

Подведем итоги сейчас:

• Очевидно, что скалярное произведение определяется только между векторами одинаковой длины.
• Таким образом, чтобы скалярное произведение между строкой и столбцом было действительным — при умножении двух матриц — вам нужно, чтобы они обе имели одинаковое количество элементов.
• В приведенном выше общем примере каждая строка в матрице A состоит из n элементов. И каждый столбец в матрице B также имеет n элементов.

Если присмотреться, n — это количество столбцов в матрице A, а также количество строк в матрице B. И именно поэтому вам нужно, чтобы количество столбцов в матрице A было равно числу строк в матрице B .

Я надеюсь, вы понимаете, что условие умножения матриц выполняется и как получить каждый элемент в матрице произведения.

Давайте приступим к написанию кода Python для умножения двух матриц.

Напишите пользовательскую функцию Python для умножения матриц

В качестве первого шага давайте напишем пользовательскую функцию для умножения матриц.

Эта функция должна делать следующее:

• Примите две матрицы, A и B, в качестве входных параметров.
• Проверьте, допустимо ли матричное умножение между A и B.
• Если допустимо, умножьте две матрицы A и B и верните матрицу произведения C.
• В противном случае вернуть сообщение об ошибке, что матрицы A и B нельзя перемножить.

Шаг 1. Сгенерируйте две матрицы целых чисел, используя функцию NumPy random.randint() . Вы также можете объявить матрицы как вложенные списки Python.

 import numpy as np np.random.seed(27) A = np.random.randint(1,10,size = (3,3)) B = np.random.randint(1,10,size = (3,2)) print(f"Matrix A:\n {A}\n") print(f"Matrix B:\n {B}\n") # Output Matrix A: [[4 9 9] [9 1 6] [9 2 3]] Matrix B: [[2 2] [5 7] [4 4]]

Шаг 2: Идите вперед и определите multiply_matrix(A,B) . Эта функция принимает две матрицы A и B в качестве входных данных и возвращает матрицу произведения C , если умножение матриц допустимо.

 def multiply_matrix(A,B): global C if A.shape[1] == B.shape[0]: C = np.zeros((A.shape[0],B.shape[1]),dtype = int) for row in range(rows): for col in range(cols): for elt in range(len(B)): C[row, col] += A[row, elt] * B[elt, col] return C else: return "Sorry, cannot multiply A and B."

Разбор определения функции

Приступим к разбору определения функции.

Объявите C как глобальную переменную : по умолчанию все переменные внутри функции Python имеют локальную область видимости . И вы не можете получить к ним доступ извне функции. Чтобы сделать матрицу произведения C доступной извне, нам придется объявить ее как глобальную переменную. Просто добавьте квалификатор global перед именем переменной.

Проверьте правильность умножения матриц: используйте атрибут shape , чтобы проверить, можно ли умножить A и B. Для любого массива arr arr.shape[0] и arr.shape[1] дают количество строк и столбцов соответственно. Итак if A.shape[1] == B.shape[0] проверяет, действительно ли матричное умножение. Только если это условие True , будет вычислена матрица продукта. В противном случае функция возвращает сообщение об ошибке.

Используйте вложенные циклы для вычисления значений: чтобы вычислить элементы результирующей матрицы, мы должны перебирать строки матрицы A, и внешний цикл for делает это. Внутренний цикл for помогает нам пройти по столбцу матрицы B. А самый внутренний цикл for помогает получить доступ к каждому элементу в выбранном столбце.

️ Теперь, когда мы узнали, как работает функция Python для умножения матриц, давайте вызовем функцию с матрицами A и B, которые мы сгенерировали ранее.

 multiply_matrix(A,B) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

Поскольку умножение матриц между A и B допустимо, multiply_matrix() возвращает матрицу произведения C.

Используйте понимание вложенных списков Python для умножения матриц

В предыдущем разделе вы написали функцию Python для умножения матриц. Теперь вы увидите, как можно использовать вложенные списки, чтобы сделать то же самое.

Вот понимание вложенного списка для умножения матриц.

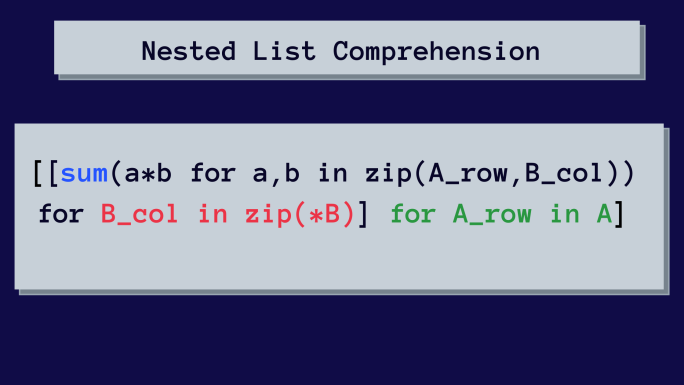
Сначала это может показаться сложным. Но мы будем шаг за шагом разбирать понимание вложенного списка.

Давайте сосредоточимся на понимании одного списка за раз и определим, что оно делает.

Мы будем использовать следующий общий шаблон для понимания списка:

 [<do-this> for <item> in <iterable>] where, <do-this>: what you'd like to do—expression or operation <item>: each item you'd like to perform the operation on <iterable>: the iterable (list, tuple, etc.) that you're looping through

️ Ознакомьтесь с нашим руководством «Понимание списков в Python» — с примерами, чтобы получить более глубокое понимание.

Прежде чем продолжить, обратите внимание, что мы хотели бы построить результирующую матрицу C по одной строке за раз.

Объяснение понимания вложенных списков

Шаг 1: вычислить одно значение в матрице C

Учитывая строку i матрицы A и столбец j матрицы B, приведенное ниже выражение дает запись с индексом (i, j) в матрице C.

 sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returns an iterator of tuples # If A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returns (a1, b1), (a2, b2), and so on

Если i = j = 1 выражение вернет элемент c_11 матрицы C. Таким образом, вы можете получить один элемент в одной строке таким образом.

Шаг 2: Постройте одну строку в матрице C

Наша следующая цель — построить целый ряд.

Для строки 1 в матрице A вам нужно перебрать все столбцы в матрице B, чтобы получить одну полную строку в матрице C.

Вернитесь к шаблону понимания списка.

• Замените <do-this> выражением из шага 1, потому что это то, что вы хотите сделать.
• Затем замените <item> на B_col каждый столбец в матрице B.
• Наконец, замените <iterable> на zip(*B) — список, содержащий все столбцы матрицы B.

А вот и первое понимание списка.

 [sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * is the unzipping operator # zip(*B) returns a list of columns in matrix B

Шаг 3: Постройте все строки и получите матрицу C

Далее вам нужно будет заполнить матрицу произведения C, вычислив остальные строки.

И для этого вам нужно перебрать все строки в матрице A.

Вернитесь к пониманию списка еще раз и сделайте следующее.

• Замените <do-this> на понимание списка из шага 2. Вспомните, что мы вычислили целую строку на предыдущем шаге.
• Теперь замените <item> на A_row каждую строку в матрице A.
• И ваш <iterable> — это сама матрица A, когда вы перебираете ее строки.

И вот наше окончательное понимание вложенного списка.

 [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]

Пришло время проверить результат!

 # cast into NumPy array using np.array() C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Если вы присмотритесь, это эквивалентно вложенным циклам for, которые мы использовали ранее, только более лаконично.

Вы также можете сделать это более эффективно, используя некоторые встроенные функции. Давайте узнаем о них в следующем разделе.

Используйте NumPy matmul() для умножения матриц в Python

np.matmul() принимает две матрицы в качестве входных данных и возвращает произведение, если умножение матриц между входными матрицами допустимо .

 C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Обратите внимание, насколько этот метод проще, чем два метода, которые мы изучили ранее. На самом деле, вместо np.matmul() вы можете использовать эквивалентный оператор @, и мы сразу это увидим.

Как использовать оператор @ в Python для умножения матриц

В Python @ — это бинарный оператор, используемый для умножения матриц.

Он работает с двумя матрицами и, как правило, с N-мерными массивами NumPy и возвращает матрицу произведения.

Примечание. Для использования оператора @ вам потребуется Python 3.5 и более поздние версии.

Вот как вы можете его использовать.

 C = [email protected] print(C) # Output array([[ 89, 107], [ 47, 49], [ 40, 44]])

Обратите внимание, что матрица произведения C такая же, как та, которую мы получили ранее.

Можете ли вы использовать np.dot() для умножения матриц?

Если вы когда-либо сталкивались с кодом, который использует np.dot() для умножения двух матриц, вот как это работает.

 C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]

Вы увидите, что np.dot(A, B) также возвращает ожидаемую матрицу продукта.

Однако, согласно документам NumPy, вы должны использовать np.dot() только для вычисления скалярного произведения двух одномерных векторов, а не для умножения матриц.

Напомним из предыдущего раздела, что элемент с индексом (i, j) матрицы произведения C является скалярным произведением строки i матрицы A и столбца j матрицы B.

Поскольку NumPy неявно передает эту операцию скалярного произведения всем строкам и всем столбцам, вы получаете результирующую матрицу произведения. Но чтобы ваш код был читабельным и чтобы избежать двусмысленности, используйте вместо этого np.matmul() или оператор @ .

Вывод

В этом уроке вы узнали следующее.

• Условие правильности умножения матриц: количество столбцов в матрице A = количеству строк в матрице B .
• Как написать пользовательскую функцию Python, которая проверяет правильность умножения матриц и возвращает матрицу произведения. В теле функции используются вложенные циклы for.
• Далее вы узнали, как использовать вложенные списки для умножения матриц. Они более лаконичны, чем циклы for, но подвержены проблемам с читабельностью.
• Наконец, вы узнали, как использовать встроенную функцию NumPy np.matmul() для умножения матриц и как это наиболее эффективно с точки зрения скорости.
• Вы также узнали об операторе @ для умножения двух матриц в Python.

На этом мы завершаем обсуждение умножения матриц в Python. В качестве следующего шага узнайте, как проверить, является ли число простым в Python. Или решить интересные задачи на строки Python.

Приятного обучения!