Python'da Floor Division Nasıl Yapılır?
Yayınlanan: 2022-11-02Bu eğitimde, Python'da kat bölme işlemini nasıl yapacağınızı öğreneceksiniz. Python'un // operatörünü, Python'un matematik modülündeki kat işlevini ve daha fazlasını kod örnekleriyle birlikte kullanacaksınız.
Python'daki aritmetik operatörlere genel bir bakışla başlayacağız ve kat bölme operatörünün // nasıl çalıştığını öğreneceğiz. Ardından, kat bölme işlemini gerçekleştirmek için matematik ve operatör modüllerindeki fonksiyonlar dahil olmak üzere diğer eşdeğer yöntemleri nasıl kullanacağımızı öğreneceğiz.
Başlayalım…
Python'da Aritmetik Operatörler
Python'da, int ve float veri türlerinde sayılar üzerinde basit aritmetik işlemler gerçekleştirmek için aritmetik operatörleri kullanabilirsiniz. Bu operatörler işlenenler (sayılar) üzerinde hareket eder ve işlemin sonucunu döndürür.

Aşağıdaki tablo Python'daki aritmetik operatörleri ve nasıl çalıştıklarını özetlemektedir:
| Şebeke | Sözdizimi | Sonuç |
| Ekleme (+) | num1+num2 | num1 ve num2 toplamını döndürür |
| çıkarma (-) | num1-num2 | num1 ve num2 arasındaki farkı döndürür |
| Çarpma işlemi (*) | num1*num2 | num1 ve num2 ürününü döndürür |
| Üs (**) | num1**num2 | num2 sonucunu num1 yükselterek döndürür; num1 num2 |
| Bölüm (/) | num1/num2 | num1 bölündüğünde sonucu num2 - kesirli kısım dahil |
| Kat bölümü (/) | num1//num2 | num2 num1 bölündüğünde bölümü döndürür |
| Modül (%) | num1 % num2 | num2 num1 bölümünden kalanı döndürür |
Bu aritmetik operatörleri kullanan birkaç örnek alalım. Bu örnekleri Python REPL'de veya Geekflare'nin çevrimiçi Python düzenleyicisinde deneyebilirsiniz.
>>> num1 = 18 >>> num2 = 5 >>> num1 + num2 23 >>> num1 - num2 13 >>> num1 * num2 90 >>> num1 ** num2 1889568 Bu örnekte, num1 18 ve num2 5'tir. Bölme işlemi num1/num2 kesirli kısmı içeren sonucu döndürür.
5 sayısı üç kez 18'e girer ve kalan üç kalır. Bu nedenle, kat bölme işlemi, num1//num2 , bölüm 3'ü verirken, modulo operatörü kalanı verir - bu durumda da 3'tür.
>>> num1/num2 3.6 >>> num1//num2 3 >>> num1 % num2 3Bu size bölme, kat bölme ve modulo operatörlerinin nasıl çalıştığı hakkında bir fikir verecektir. Ardından, kat bölme operatörünü ayrıntılı olarak öğreneceğiz.
️ Python 2'de bölme işlemi (/) sonucu en yakın tamsayıya kısaltır—Python 3'teki kat bölme işlemine benzer.
// Operatörünü Kullanarak Kat Bölme

Temettü ve bölen içeren bir bölme işlemi düşünün. num1/num2 içinde, num1 bölen ve num2 bölendir. num1 ve num2 kat bölme işlemini gerçekleştirmek için num1//num2 kullanın.
Kat bölme operatörü (//), işlenenlerin veri türlerine bağlı olarak bölme işleminin bölümünü tam sayı veya kayan noktalı sayı olarak döndürür.
Kat bölme operatörü, cevabın her zaman bir tam sayı olmasını sağlamaz. Bölünen ( num1 ) veya bölen ( num2 ) bir kayan nokta ise, num1//num2 sonucu bir kayan noktadır. İşte birkaç örnek.
>>> 18.0//5 3.0 >>> 10.0//4 2.0 >>> 15//4.0 3.0 Sonucun bir tamsayı olması gerekiyorsa, bunu int() işlevini kullanarak açıkça bir tamsayıya dönüştürmeniz gerekir:
>>> int(18.0//5) 3 >>> int(10.0//4) 2 >>> int(15//4.0) 3Kaputun Altında Ne Olur?
Kat bölme operatörünü // kullandığınızda, özel yöntem (dunder yöntemi de denir) __floordiv__() çağrılır. Bu nedenle, aşağıda gösterildiği gibi herhangi bir tamsayı veya kayan nokta sayısında __floordiv__() yöntemini de kullanabilirsiniz:
num1 = 18 num2 = 5 num1.__floordiv__(num2) # Output: 3Operatör.floordiv() Kullanarak Kat Bölme

Python'da kat bölme işlemini gerçekleştirmek için operator modülündeki floordiv() işlevini de kullanabilirsiniz.
Python'un operatör modülü, tüm aritmetik işlemleri gerçekleştirebilen etkin fonksiyonların tanımlarını içerir. Bu nedenle, kat bölme işlemini gerçekleştirmek için, // operatörü yerine operatör modülündeki floordiv() işlevini de kullanabilirsiniz.
Operatör modülünden floordiv() işlevinin kullanılması, kat bölme operatörünün kullanılmasına eşdeğerdir.
>>> import operator >>> operator.floordiv(18,5) # Output: 3 >>> operator.floordiv(12,5.0) # Output: 2.0Math.floor() Kullanarak Kat Bölme
Zemin Fonksiyonu Nasıl Çalışır?
Matematikte,
floor()işlevi girdi olarak herhangi bir gerçekxsayısını alır ve bir tamsayı (sonuç) döndürür. Bu sonuç, x gerçek sayısından küçük veya ona eşit olan en büyük tam sayıdır .
Bunu daha iyi anlamak için birkaç örnek alalım ve bu sayıları sayı doğrusu üzerinde görselleştirelim.
Örnek 1 : 2.3 sayısını düşünün. 2,3'ten küçük veya eşit olan en büyük tam sayı 2'dir; yani kat(2.3) 2 değerini döndürür.
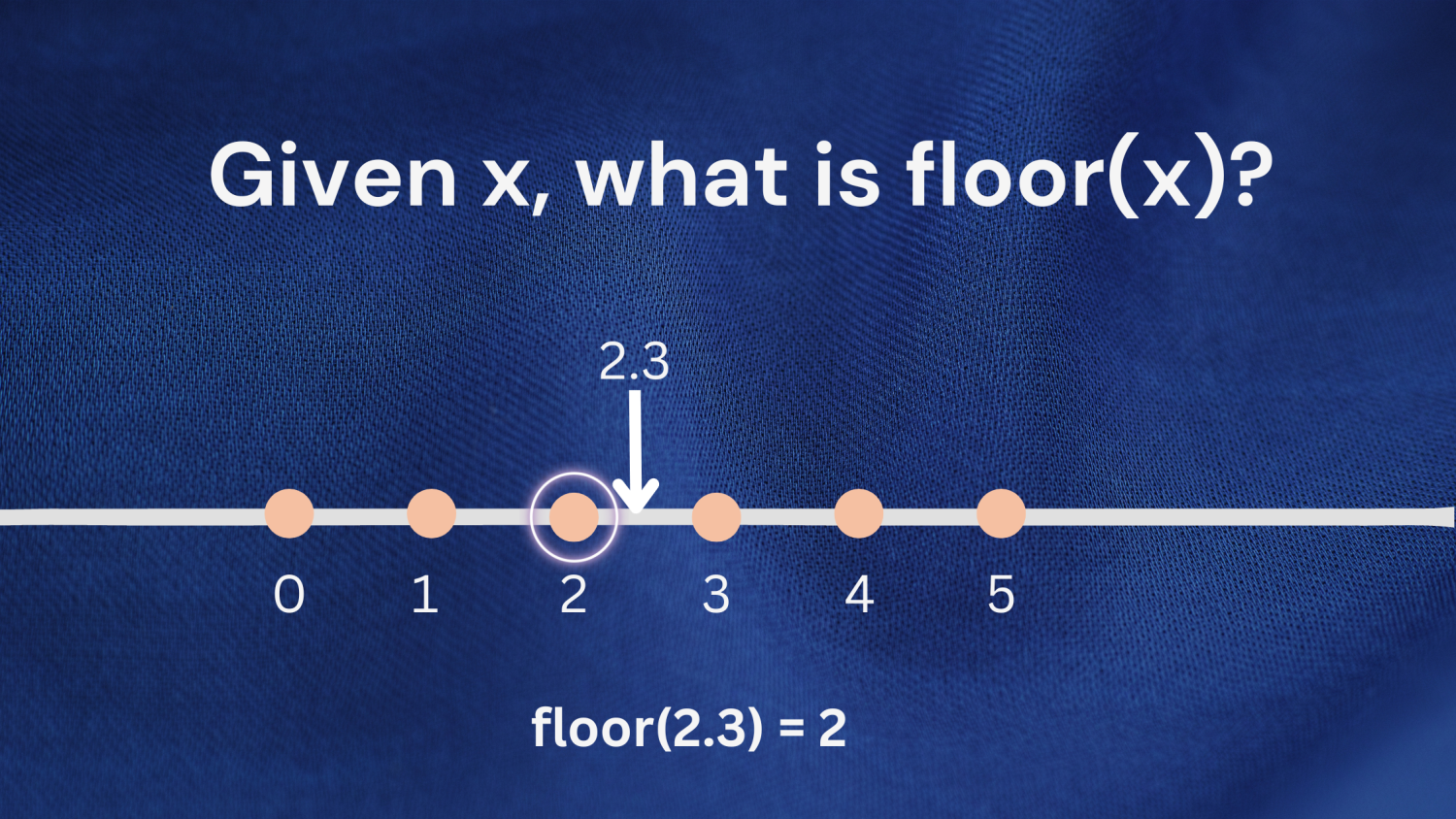
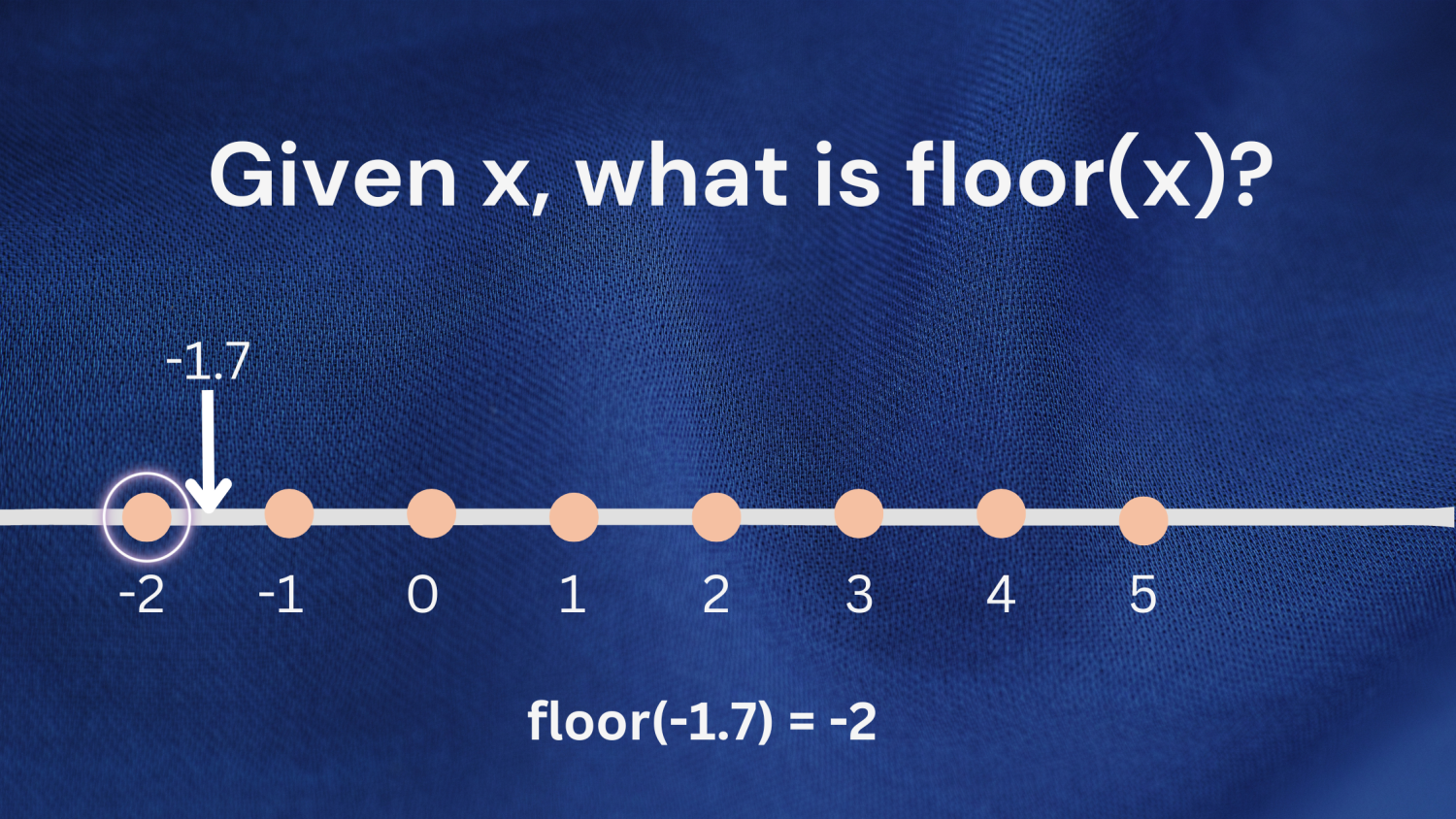
Örnek 2: Negatif sayılarla çalışırken de aynı tanımı uygulayabilirsiniz. -1.7 sayısını düşünün. -1,7'den küçük veya eşit olan en büyük tam sayı -2'dir; yani kat(-1.7) -2 döndürür.

Matematik modülündeki floor() işlevini kullanarak yukarıdaki sonuçları doğrulayalım.
>>> from math import floor >>> floor(2.3) 2 >>> floor(-1.7) -2 Kat bölme işlemini gerçekleştirmek için, argüman olarak num1/num2 ile floor() işlevini çağırabilirsiniz. Sonucu en yakın tam sayıya yuvarladığı veya yuvarladığı için, kat bölme işlemine eşdeğerdir.
floor() işlevini math modülünden gösterildiği gibi açıkça içe aktarabilirsiniz:
from math import floor num1 = 18 num2 = 5 floor(num1/num2) # Output: 3 Alternatif olarak, yalnızca math modülünü içe aktarabilir ve ardından math.floor() kullanarak floor() işlevine erişebilirsiniz.
import math num1 = 18 num2 = 5 math.floor(num1/num2) # Output: 3 Operatör modülündeki floordiv() işlevinden ve kat bölme operatöründen // farklı olarak, math.floor(num1/num2) kullanılması sonucun bir tamsayı olmasını sağlar. Bu yöntem kodu okunabilir hale getirir ve tip döküm adımını ortadan kaldırır.
import math num1 = 18.0 num2 = 5 math.floor(num1/num2) # Output: 3Python'da Kat Bölümü Örnekleri

Tartışmamızı pratik bir örnekle sonlandıralım: İkili arama.
İkili arama, n'nin dizinin boyutu olduğu O(log n) zamanında sıralanmış diziler aracılığıyla bir hedef öğeyi aramanıza izin veren verimli bir arama algoritmasıdır.
Bu algoritma, her adımda arama aralığını yarıya bölerek çalışır. Bu, aralığın orta noktasının hedefle eşleşmesine (arama, eşleşme bulunduğunda sona erer!) veya hedeften küçük veya büyük olmasına bağlı olarak yapılır. Dizinin boyutu her adımda yarıya indirildiğinden, orta nokta her zaman bir tamsayı olarak değerlendirilmez.
itemlist = [5,7,18,21,34,45] item = 7 İkili arama algoritmasının aşağıdaki uygulamasını düşünün. binary_search() işlevi bir sayı ( item ) ve bir liste ( itemlist listesi) alır ve öğe listesinde item oluşumunu itemlist .
-
itembulunursa, işlev,itemoluştuğu dizini döndürür. - Aksi takdirde,
Nonedöndürür.
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use normal division instead of floor division midPt = (lowerIdx + upperIdx)/ 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return None Bu uygulama, arama ilerledikçe midPt'nin bir tamsayı olarak değerlendirilmemesini hesaba midPt dışında işlevsel olarak doğrudur.
binary_search(item,itemlist) Fonksiyonu çağırırsak, liste indekslerinin yüzer değil tamsayı veya dilim olması gerektiğini belirten bir TypeError ile karşılaşırız.
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-3-a5f12ebc3145> in <module> ----> 1 binary_search(item,itemlist) <ipython-input-2-524ef6900b1f> in binary_search(item, itemlist) 12 13 # if item is found, return the index ---> 14 if itemlist[midPt] == item: 15 return midPt 16 # otherwise get the next midpoint TypeError: list indices must be integers or slices, not floatKat bölme operatörünü kullanmak için fonksiyon tanımını değiştiriyoruz:
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use floor division midPt = (lowerIdx + upperIdx)// 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return Noneİşlev, bir dizin olan 7 öğesinin bulunduğu dizini döndürür.
binary_search(item,itemlist) # Output: 1Çözüm
Umarım bu eğitim Python'da kat bölme işlemini nasıl yapacağınızı anlamanıza yardımcı olmuştur. İşte öğrendiğiniz farklı yöntemlerin bir özeti:
- Python'da bir operatör b , operatör tarafından işlenen olarak a ve b ile tanımlanan işlemi gerçekleştirir ve işlemin sonucunu döndürür.
- Python'un kat bölme operatörünü kullanabilirsiniz //; a//b , a/b bölme işleminin bölümünü döndürür.
- Alternatif olarak, a//b sonucunu almak için Python'un operatör modülünde tanımlanan eşdeğer floordiv() işlevini şu sözdizimi ile kullanabilirsiniz: operatör.floordiv(a,b) .
- Yukarıdaki yöntemlerin tümü bölümü döndürür, ancak veri türü, a ve b değerlerine bağlı olarak bir kayan nokta veya bir int olabilir. Bu yüzden dönüş değerini bir tam sayıya çevirmeniz gerekecek.
- Python'un matematik modülündeki floor() işlevi aynı zamanda kat bölme işlemini gerçekleştirmek için de kullanılabilir: math.floor(a,b) a//b'ye eşdeğerdir ve bir tamsayı döndürür. Sonucun bir tamsayı olmasını istediğinizde, matematik modülündeki kat işlevini kullanmayı düşünün.
Ardından, Python'da defaultdict ile nasıl çalışacağınızı öğrenin.
