So führen Sie eine Bodenteilung in Python durch
Veröffentlicht: 2022-11-02In diesem Lernprogramm erfahren Sie, wie Sie die Bodenteilung in Python durchführen. Sie verwenden den //-Operator von Python, die Floor-Funktion aus dem Math-Modul von Python und mehr – mit Codebeispielen.
Wir beginnen mit einem Überblick über arithmetische Operatoren in Python und lernen, wie der Floor Division Operator // funktioniert. Dann lernen wir, wie andere äquivalente Methoden verwendet werden, einschließlich Funktionen aus den Mathematik- und Operatormodulen, um die Stockwerksteilung durchzuführen.
Lass uns anfangen…
Arithmetische Operatoren in Python
In Python können Sie arithmetische Operatoren verwenden, um einfache arithmetische Operationen mit Zahlen der Datentypen int und float auszuführen. Diese Operatoren wirken auf Operanden (die Zahlen) und geben das Ergebnis der Operation zurück.

Die folgende Tabelle fasst die arithmetischen Operatoren in Python und ihre Funktionsweise zusammen:
| Operator | Syntax | Ergebnis |
| Zusatz (+) | num1+num2 | Gibt die Summe von num1 und num2 |
| Subtraktion (-) | num1-num2 | Gibt die Differenz zwischen num1 und num2 |
| Multiplikation (*) | num1*num2 | Gibt das Produkt von num1 und num2 |
| Potenzierung (**) | num1**num2 | Gibt das Ergebnis von num1 potenziert mit num2 ; num1 num2 |
| Aufteilung (/) | num1/num2 | Gibt das Ergebnis zurück, wenn num1 durch num2 dividiert wird – einschließlich des Bruchteils |
| Etagenaufteilung (/) | num1//num2 | Gibt den Quotienten zurück, wenn num1 durch num2 dividiert wird |
| Modulo (%) | num1 % num2 | Gibt den Rest zurück, wenn num1 durch num2 dividiert wird |
Nehmen wir ein paar Beispiele, die diese arithmetischen Operatoren verwenden. Sie können diese Beispiele in einer Python-REPL oder im Online-Python-Editor von Geekflare ausprobieren.
>>> num1 = 18 >>> num2 = 5 >>> num1 + num2 23 >>> num1 - num2 13 >>> num1 * num2 90 >>> num1 ** num2 1889568 In diesem Beispiel ist num1 18 und num2 5. Die Divisionsoperation num1/num2 gibt das Ergebnis einschließlich des Bruchteils zurück.
Die Zahl 5 geht dreimal in 18 über und lässt einen Rest von drei übrig. Daher ergibt die Floor-Division-Operation num1//num2 den Quotienten 3, während der Modulo-Operator den Rest ergibt – in diesem Fall ebenfalls 3.
>>> num1/num2 3.6 >>> num1//num2 3 >>> num1 % num2 3Dies sollte Ihnen eine Vorstellung davon vermitteln, wie die Divisions-, Floor-Divisions- und Modulo-Operatoren funktionieren. Als Nächstes lernen wir den Floor-Division-Operator im Detail kennen.
️ In Python 2 schneidet die Divisionsoperation (/) das Ergebnis auf die nächste Ganzzahl ab – ähnlich der Floor-Divisionsoperation in Python 3. In diesem Tutorial wird erläutert, wie die Floor-Divisionsoperation in Python 3.x funktioniert.
Geschossaufteilung mit dem //-Operator

Betrachten Sie eine Divisionsoperation mit einem Dividenden und einem Divisor. In num1/num2 ist num1 der Dividende und num2 der Divisor. Verwenden num1//num2 , um eine Floor-Division von num1 und num2 durchzuführen.
Der Floor-Divisionsoperator (//) gibt den Quotienten der Divisionsoperation zurück – als Ganzzahl oder als Fließkommazahl – abhängig von den Datentypen der Operanden.
Der Floor-Division-Operator stellt nicht sicher, dass die Antwort immer eine ganze Zahl ist. Wenn entweder der Dividende ( num1 ) oder der Divisor ( num2 ) ein Float ist, dann ist das Ergebnis von num1//num2 ein Float. Hier sind ein paar Beispiele.
>>> 18.0//5 3.0 >>> 10.0//4 2.0 >>> 15//4.0 3.0 Wenn das Ergebnis eine Ganzzahl sein soll, müssen Sie es mit der Funktion int() explizit in eine Ganzzahl umwandeln:
>>> int(18.0//5) 3 >>> int(10.0//4) 2 >>> int(15//4.0) 3Was passiert unter der Haube?
Wenn Sie den Floor-Division-Operator // verwenden, wird die spezielle Methode (auch Dunder-Methode genannt) __floordiv__() aufgerufen. Daher können Sie die Methode __floordiv__() auch für jede Ganzzahl oder Fließkommazahl verwenden, wie unten gezeigt:
num1 = 18 num2 = 5 num1.__floordiv__(num2) # Output: 3Floor Division mit operator.floordiv()

Um die Stockwerksteilung in Python durchzuführen, können Sie auch die Funktion floordiv() im operator verwenden.
Das Operatormodul von Python enthält die Definitionen effizienter Funktionen, die alle arithmetischen Operationen ausführen können. Daher können Sie zur Stockwerksaufteilung auch die Funktion floordiv() aus dem Operatormodul verwenden – anstelle des //-Operators.
Die Verwendung der floordiv() Funktion aus dem Operatormodul entspricht der Verwendung des Floor-Division-Operators.
>>> import operator >>> operator.floordiv(18,5) # Output: 3 >>> operator.floordiv(12,5.0) # Output: 2.0Floor Division mit math.floor()
Wie funktioniert die Bodenfunktion?
In der Mathematik nimmt die Funktion
floor()eine beliebige reelle Zahlxals Eingabe und gibt eine Ganzzahl (Ergebnis) zurück. Dieses Ergebnis ist die größte ganze Zahl , die kleiner oder gleich der reellen Zahl x ist.
Um dies besser zu verstehen, nehmen wir einige Beispiele und visualisieren diese Zahlen auf einem Zahlenstrahl.
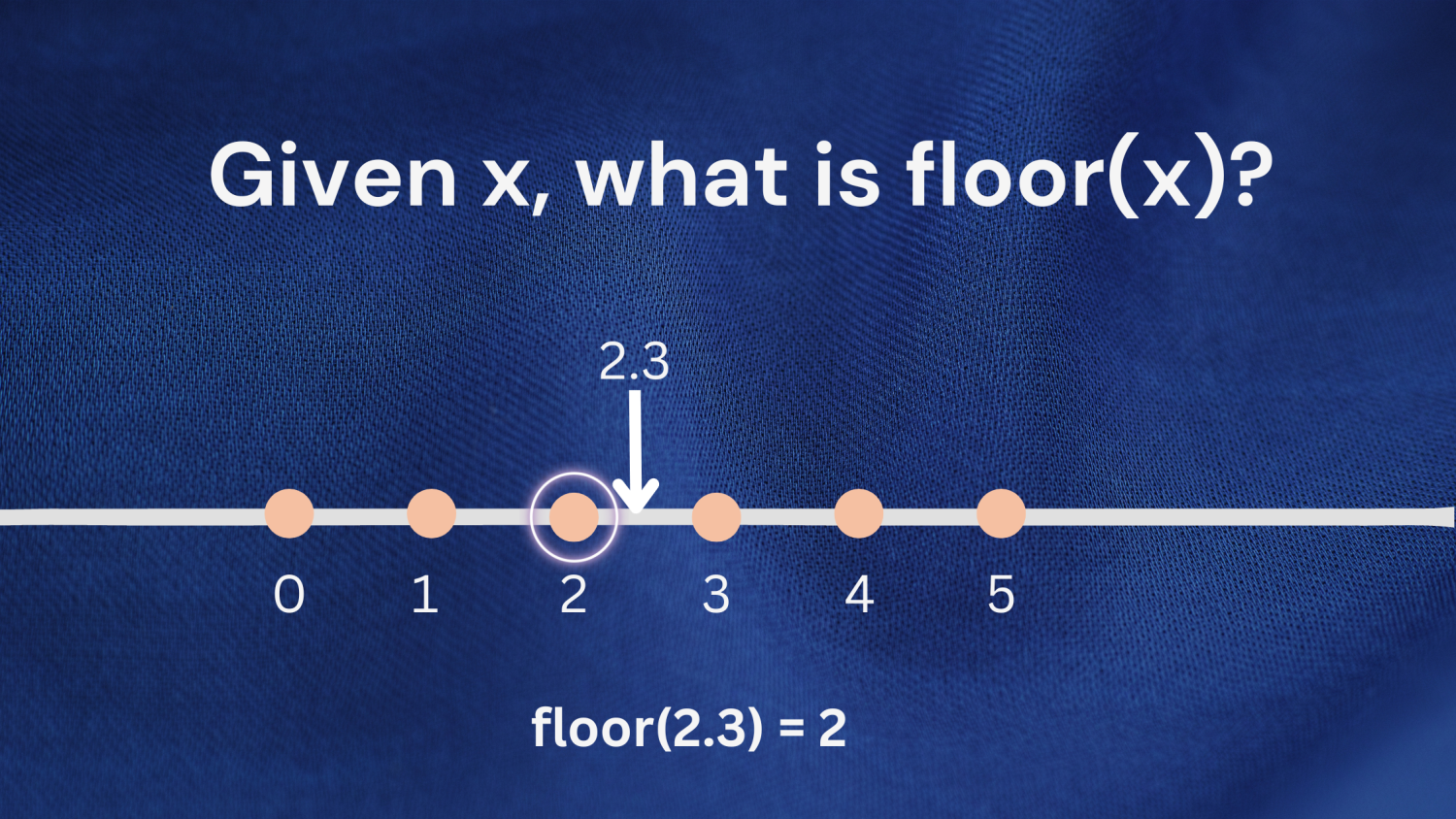
Beispiel 1 : Betrachten Sie die Zahl 2,3. Die größte ganze Zahl, die kleiner oder gleich 2,3 ist, ist 2; also gibt floor(2.3) 2 zurück.
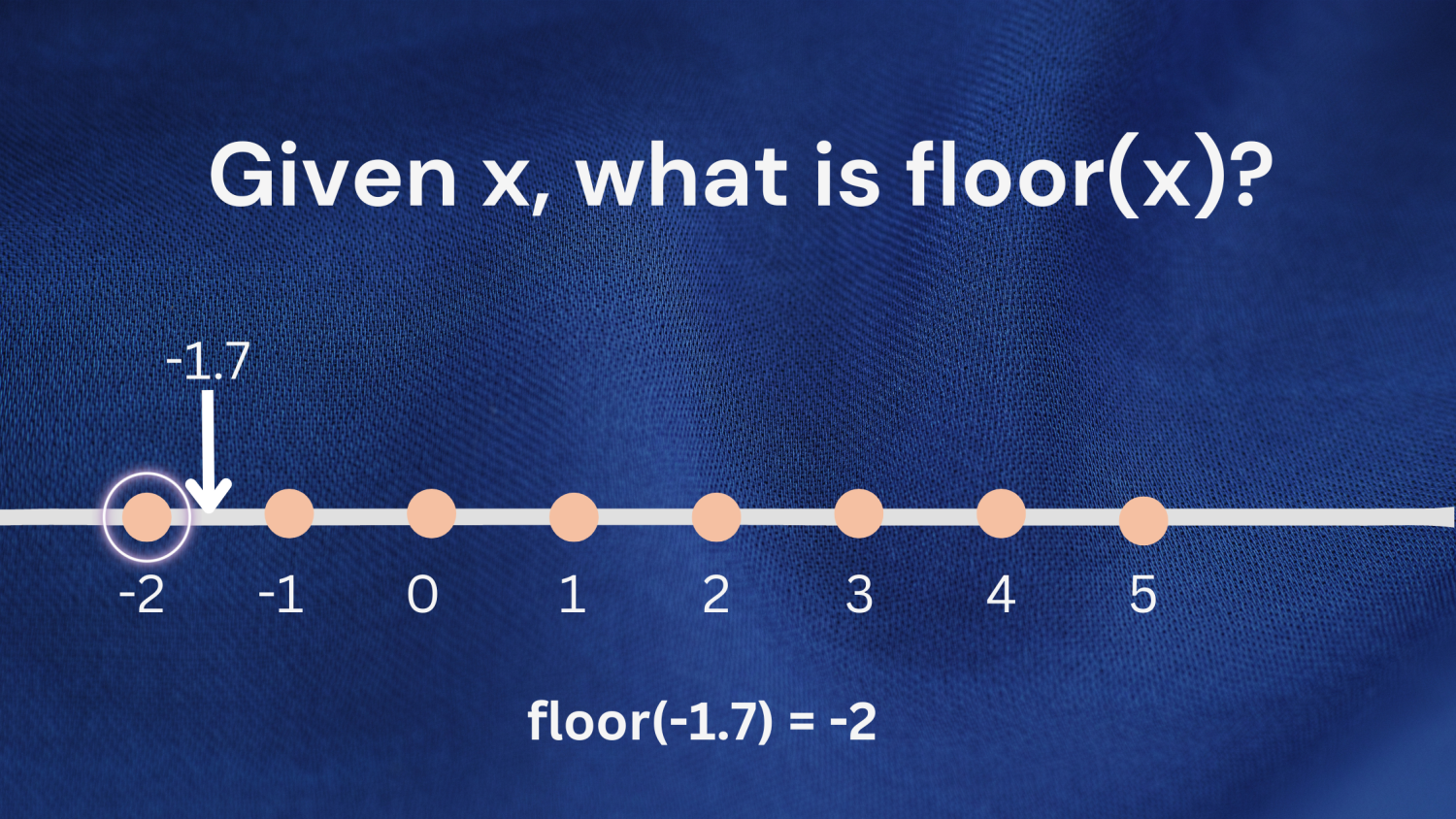
Beispiel 2: Sie können dieselbe Definition auch anwenden, wenn Sie mit negativen Zahlen arbeiten. Betrachten Sie die Zahl -1,7. Die größte Ganzzahl, die kleiner oder gleich -1,7 ist, ist -2; floor(-1.7) gibt also -2 zurück.

Lassen Sie uns die obigen Ergebnisse mit der Funktion floor() aus dem Mathematikmodul überprüfen.
>>> from math import floor >>> floor(2.3) 2 >>> floor(-1.7) -2 Um eine Floor-Division durchzuführen, können Sie die Funktion floor() mit num1/num2 als Argument aufrufen. Da es das Ergebnis auf die nächste ganze Zahl abschneidet oder abrundet, entspricht es der Floor Division Operation.
Sie können die Funktion floor() explizit aus dem math importieren, wie gezeigt:
from math import floor num1 = 18 num2 = 5 floor(num1/num2) # Output: 3 Alternativ können Sie auch nur das math -Modul importieren und dann mit math.floor() auf die Funktion floor( floor() zugreifen.
import math num1 = 18 num2 = 5 math.floor(num1/num2) # Output: 3 Anders als bei der floordiv() Funktion aus dem Operatormodul und dem Floor-Division-Operator // stellt die Verwendung von math.floor(num1/num2) sicher, dass das Ergebnis eine ganze Zahl ist. Diese Methode macht den Code lesbar und eliminiert den Typumwandlungsschritt.
import math num1 = 18.0 num2 = 5 math.floor(num1/num2) # Output: 3Beispiele für Floor Division in Python

Lassen Sie uns unsere Diskussion mit einem praktischen Beispiel abschließen: Binäre Suche.
Die binäre Suche ist ein effizienter Suchalgorithmus, mit dem Sie nach einem Zielelement durch sortierte Arrays in O(log n) -Zeit suchen können, wobei n die Größe des Arrays ist.
Dieser Algorithmus funktioniert, indem er das Suchintervall bei jedem Schritt halbiert. Dies geschieht abhängig davon, ob der Mittelpunkt des Intervalls mit dem Ziel übereinstimmt (Suche endet, wenn eine Übereinstimmung gefunden wird!) oder kleiner oder größer als das Ziel ist. Da die Größe des Arrays bei jedem Schritt um die Hälfte reduziert wird, ergibt der Mittelpunkt nicht immer eine ganze Zahl.
itemlist = [5,7,18,21,34,45] item = 7 Betrachten Sie die folgende Implementierung des binären Suchalgorithmus. Die Funktion binary_search() nimmt eine Zahl ( item ) und eine Liste ( itemlist ) entgegen und sucht nach dem Vorkommen des item in itemlist .
- Wenn das
itemgefunden wird, gibt die Funktion den Index zurück, an dem dasitemvorkommt. - Andernfalls wird
Nonezurückgegeben.
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use normal division instead of floor division midPt = (lowerIdx + upperIdx)/ 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return None Diese Implementierung ist funktional korrekt, außer dass wir nicht berücksichtigt haben, dass der midPt nicht zu einer Ganzzahl ausgewertet wird, während die Suche fortschreitet.
binary_search(item,itemlist) Wenn wir die Funktion aufrufen, stoßen wir auf einen TypeError , der besagt, dass die Listenindizes Integer oder Slices sein müssen, nicht Float.
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-3-a5f12ebc3145> in <module> ----> 1 binary_search(item,itemlist) <ipython-input-2-524ef6900b1f> in binary_search(item, itemlist) 12 13 # if item is found, return the index ---> 14 if itemlist[midPt] == item: 15 return midPt 16 # otherwise get the next midpoint TypeError: list indices must be integers or slices, not floatWir modifizieren die Funktionsdefinition, um den Floor-Division-Operator zu verwenden:
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use floor division midPt = (lowerIdx + upperIdx)// 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return NoneDie Funktion gibt den Index zurück, an dem das Element 7 gefunden wird, also Index eins.
binary_search(item,itemlist) # Output: 1Fazit
Ich hoffe, dieses Tutorial hat Ihnen geholfen zu verstehen, wie Sie die Bodenteilung in Python durchführen. Hier ist eine Zusammenfassung der verschiedenen Methoden, die Sie gelernt haben:
- In Python führt ein Operator b die durch den Operator definierte Operation mit a und b als Operanden aus und gibt das Ergebnis der Operation zurück.
- Sie können Pythons Floor-Division-Operator // verwenden; a//b gibt den Quotienten der Divisionsoperation a/b zurück.
- Alternativ können Sie die entsprechende Funktion floordiv() verwenden, die im Operatormodul von Python mit der folgenden Syntax definiert ist: operator.floordiv(a,b) , um das Ergebnis von a//b zu erhalten.
- Alle oben genannten Methoden geben den Quotienten zurück, aber der Datentyp kann abhängig von den Werten von a und b Float oder Int sein. Sie müssen also den Rückgabewert in eine Ganzzahl umwandeln.
- Die Funktion floor() aus dem Math-Modul von Python kann auch verwendet werden, um eine Floor-Division durchzuführen: math.floor(a,b) ist äquivalent zu a//b und gibt eine ganze Zahl zurück. Wenn Sie möchten, dass das Ergebnis eine Ganzzahl ist, sollten Sie die Floor-Funktion aus dem Mathematikmodul verwenden.
Als Nächstes erfahren Sie, wie Sie mit defaultdict in Python arbeiten.
