Jak wykonać podział podłóg w Pythonie
Opublikowany: 2022-11-02W tym samouczku dowiesz się, jak przeprowadzić podział pięter w Pythonie. Użyjesz operatora // Pythona, funkcji floor z modułu matematycznego Pythona i nie tylko – z przykładami kodu.
Zaczniemy od przeglądu operatorów arytmetycznych w Pythonie i dowiemy się, jak działa operator dzielenia pięter //. Następnie nauczymy się korzystać z innych równoważnych metod, w tym funkcji z modułów matematycznych i operatorskich, aby dokonać podziału pięter.
Zacznijmy…
Operatory arytmetyczne w Pythonie
W Pythonie można używać operatorów arytmetycznych do wykonywania prostych operacji arytmetycznych na liczbach o typach danych int i float . Operatory te działają na operandach (liczby) i zwracają wynik operacji.

Poniższa tabela podsumowuje operatory arytmetyczne w Pythonie i sposób ich działania:
| Operator | Składnia | Wynik |
| Dodatek (+) | num1+num2 | Zwraca sumę num1 i num2 |
| Odejmowanie (-) | num1-num2 | Zwraca różnicę między num1 a num2 |
| Mnożenie (*) | num1*num2 | Zwraca iloczyn liczby num1 i num2 |
| Potęgowanie (**) | num1**num2 | Zwraca wynik num1 podniesiony do potęgi num2 ; num1 num2 |
| Podział (/) | num1/num2 | Zwraca wynik, gdy num1 jest dzielona przez num2 – łącznie z częścią ułamkową |
| Podział piętra (/) | num1//num2 | Zwraca iloraz, gdy num1 jest dzielona przez num2 |
| Moduł (%) | num1 % num2 | Zwraca resztę z dzielenia num1 przez num2 |
Weźmy kilka przykładów, które używają tych operatorów arytmetycznych. Możesz wypróbować te przykłady w Pythonie REPL lub w internetowym edytorze Pythona Geekflare.
>>> num1 = 18 >>> num2 = 5 >>> num1 + num2 23 >>> num1 - num2 13 >>> num1 * num2 90 >>> num1 ** num2 1889568 W tym przykładzie num1 to 18, a num2 to 5. Operacja dzielenia num1/num2 zwraca wynik zawierający część ułamkową.
Liczba 5 przechodzi w 18 trzy razy, pozostawiając resztę trzech. Dlatego operacja dzielenia piętra, num1//num2 , daje iloraz 3, podczas gdy operator modulo daje resztę – w tym przypadku również 3.
>>> num1/num2 3.6 >>> num1//num2 3 >>> num1 % num2 3Powinno to dać wyobrażenie o tym, jak działają operatory dzielenia, dzielenia pięter i modulo. Następnie dowiemy się szczegółowo o operatorze podziału pięter.
️ W Pythonie 2 operacja dzielenia (/) obcina wynik do najbliższej liczby całkowitej — podobnie do operacji dzielenia pięter w Pythonie 3. W tym samouczku omówiono działanie operacji dzielenia pięter w Pythonie 3.x.
Podział piętra za pomocą // operatora

Rozważ operację dzielenia z dywidendą i dzielnikiem. W num1/num2 , num1 to dzielna, a num2 to dzielnik. Aby dokonać podziału pięter num1 i num2 , użyj num1//num2 .
Operator dzielenia podłogi (//) zwraca iloraz operacji dzielenia — jako liczbę całkowitą lub liczbę zmiennoprzecinkową — w zależności od typów danych operandów.
Operator dzielenia piętra nie gwarantuje, że odpowiedź jest zawsze liczbą całkowitą. Jeśli dzielna ( num1 ) lub dzielnik ( num2 ) jest liczbą zmiennoprzecinkową, to wynik num1//num2 jest liczbą zmiennoprzecinkową. Oto kilka przykładów.
>>> 18.0//5 3.0 >>> 10.0//4 2.0 >>> 15//4.0 3.0 Jeśli chcesz, aby wynik był liczbą całkowitą, musisz jawnie rzutować go na liczbę całkowitą za pomocą funkcji int() :
>>> int(18.0//5) 3 >>> int(10.0//4) 2 >>> int(15//4.0) 3Co dzieje się pod maską?
Kiedy używasz operatora podziału pięter //, wywoływana jest specjalna metoda (zwana również metodą dunder) __floordiv__() . Dlatego możesz również użyć metody __floordiv__() na dowolnej liczbie całkowitej lub zmiennoprzecinkowej, jak pokazano poniżej:
num1 = 18 num2 = 5 num1.__floordiv__(num2) # Output: 3Podział piętra za pomocą operator.floordiv()

Aby dokonać podziału pięter w Pythonie, możesz również użyć funkcji floordiv() w module operator .
Moduł operatora Pythona zawiera definicje wydajnych funkcji, które mogą wykonywać wszystkie operacje arytmetyczne. Dlatego do podziału pięter można również użyć funkcji floordiv() z modułu operator – zamiast operatora //.
Użycie funkcji floordiv() z modułu operator jest równoważne użyciu operatora dzielenia pięter.
>>> import operator >>> operator.floordiv(18,5) # Output: 3 >>> operator.floordiv(12,5.0) # Output: 2.0Podział piętra za pomocą funkcji math.floor()
Jak działa funkcja podłogi?
W matematyce funkcja
floor()przyjmuje dowolną liczbę rzeczywistąxjako dane wejściowe i zwraca liczbę całkowitą (wynik). Ten wynik jest największą liczbą całkowitą , która jest mniejsza lub równa liczbie rzeczywistej x.
Aby lepiej to zrozumieć, weźmy kilka przykładów i zwizualizujmy te liczby na osi liczbowej.
Przykład 1 : Rozważmy liczbę 2.3. Największa liczba całkowita mniejsza lub równa 2,3 to 2; więc piętro (2.3) zwróci 2.
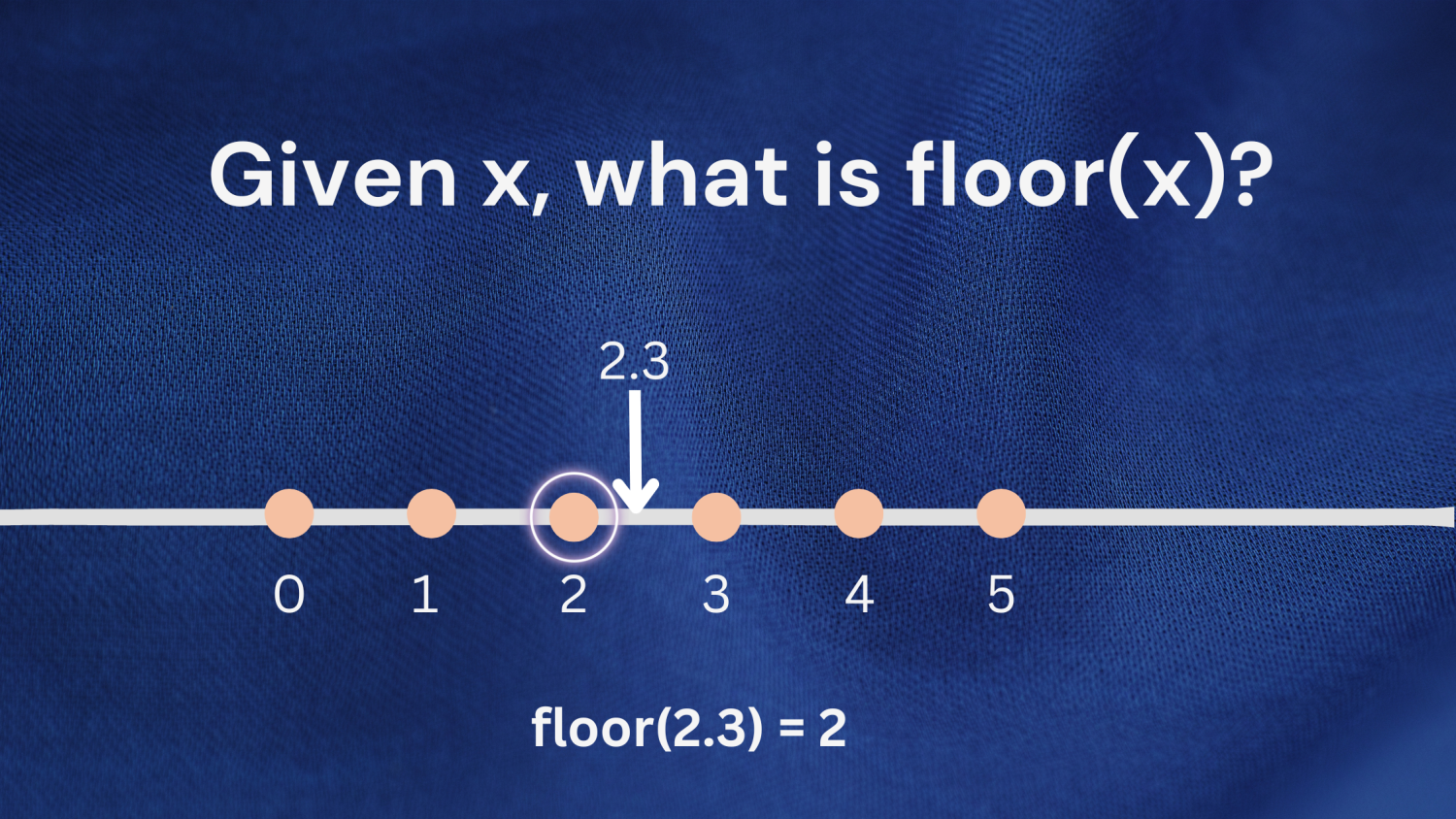
Przykład 2: Tę samą definicję można zastosować również podczas pracy z liczbami ujemnymi. Rozważ liczbę -1,7. Największa liczba całkowita mniejsza lub równa -1,7 to -2; więc piętro (-1.7) zwróci -2.

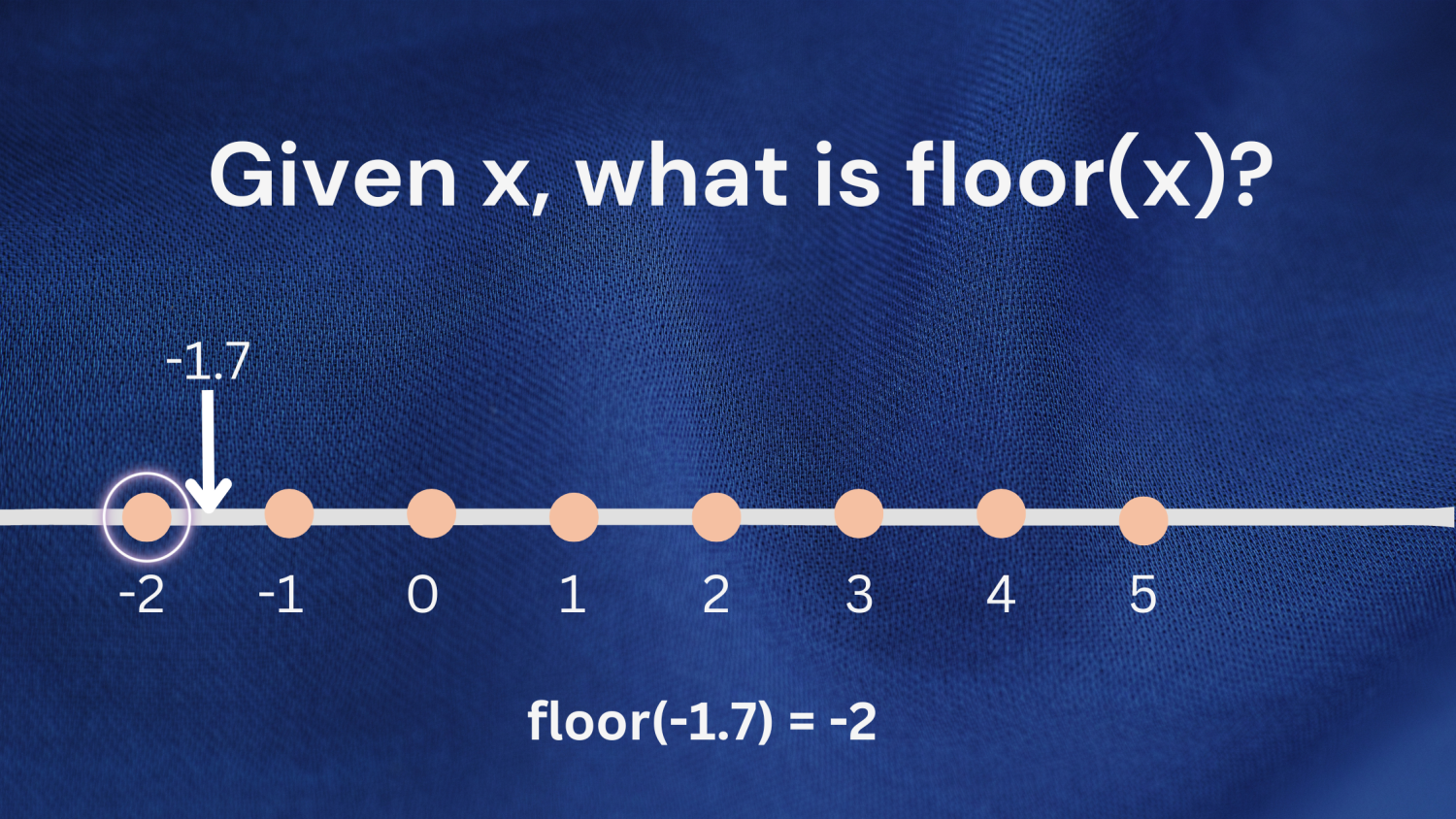
Zweryfikujmy powyższe wyniki za pomocą funkcji floor() z modułu math.
>>> from math import floor >>> floor(2.3) 2 >>> floor(-1.7) -2 Aby dokonać podziału pięter, możesz wywołać funkcję floor() z argumentem num1/num2 . Gdy obcina lub zaokrągla wynik do najbliższej liczby całkowitej, jest to równoważne operacji dzielenia podłogi.
Możesz jawnie zaimportować funkcję floor() z modułu math , jak pokazano:
from math import floor num1 = 18 num2 = 5 floor(num1/num2) # Output: 3 Alternatywnie możesz również zaimportować tylko moduł math , a następnie uzyskać dostęp do funkcji floor() za pomocą math.floor() .
import math num1 = 18 num2 = 5 math.floor(num1/num2) # Output: 3 W przeciwieństwie do funkcji floordiv() z modułu operatora i operatora dzielenia pięter //, użycie math.floor(num1/num2) zapewnia, że wynik jest liczbą całkowitą. Ta metoda sprawia, że kod jest czytelny i eliminuje krok rzutowania typu.
import math num1 = 18.0 num2 = 5 math.floor(num1/num2) # Output: 3Przykłady podziału pięter w Pythonie

Zakończmy naszą dyskusję praktycznym przykładem: Wyszukiwanie binarne.
Wyszukiwanie binarne to wydajny algorytm wyszukiwania, który umożliwia wyszukiwanie elementu docelowego za pomocą posortowanych tablic w czasie O(log n) , gdzie n jest rozmiarem tablicy.
Ten algorytm działa poprzez podzielenie interwału wyszukiwania na połowę na każdym kroku. Odbywa się to w zależności od tego, czy punkt środkowy interwału pasuje do celu (wyszukiwanie kończy się po znalezieniu dopasowania!) lub jest mniejszy lub większy od celu. Ponieważ rozmiar tablicy jest zmniejszany o połowę na każdym kroku, punkt środkowy nie zawsze jest liczbą całkowitą.
itemlist = [5,7,18,21,34,45] item = 7 Rozważ następującą implementację algorytmu wyszukiwania binarnego. Funkcja binary_search() pobiera liczbę ( item ) i listę ( itemlist ) i wyszukuje wystąpienie item w itemlist .
- Jeśli
itemzostanie znaleziony, funkcja zwraca indeks, w którymitemwystępuje. - W przeciwnym razie zwraca
None.
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use normal division instead of floor division midPt = (lowerIdx + upperIdx)/ 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return None Ta implementacja jest funkcjonalnie poprawna, z wyjątkiem tego, że nie uwzględniliśmy, że midPt nie jest oceniany jako liczba całkowita w trakcie wyszukiwania.
binary_search(item,itemlist) Jeśli wywołamy funkcję, natkniemy się na TypeError stwierdzający, że indeksy listy muszą być liczbami całkowitymi lub wycinkami, a nie pływać.
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-3-a5f12ebc3145> in <module> ----> 1 binary_search(item,itemlist) <ipython-input-2-524ef6900b1f> in binary_search(item, itemlist) 12 13 # if item is found, return the index ---> 14 if itemlist[midPt] == item: 15 return midPt 16 # otherwise get the next midpoint TypeError: list indices must be integers or slices, not floatZmieniamy definicję funkcji tak, aby korzystała z operatora podziału pięter:
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use floor division midPt = (lowerIdx + upperIdx)// 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return NoneFunkcja zwraca indeks, pod którym znajduje się element 7, czyli indeks jeden.
binary_search(item,itemlist) # Output: 1Wniosek
Mam nadzieję, że ten samouczek pomógł ci zrozumieć, jak wykonać podział pięter w Pythonie. Oto podsumowanie różnych poznanych metod:
- W Pythonie operator b wykonuje operację zdefiniowaną przez operator z aib jako operandami i zwraca wynik operacji.
- Możesz użyć operatora dzielenia pięter Pythona //; a//b zwraca iloraz operacji dzielenia a/b.
- Alternatywnie możesz użyć równoważnej funkcji floordiv() zdefiniowanej w module operatora Pythona o składni: operator.floordiv(a,b), aby uzyskać wynik a//b.
- Wszystkie powyższe metody zwracają iloraz, ale typem danych może być liczba zmiennoprzecinkowa lub int w zależności od wartości a i b. Musisz więc rzucić zwracaną wartość na liczbę całkowitą.
- Funkcja floor() z modułu math Pythona może być również użyta do wykonania dzielenia pięter: math.floor(a,b) jest równoważne a//bi zwraca liczbę całkowitą. Jeśli chcesz, aby wynik był liczbą całkowitą, rozważ użycie funkcji floor z modułu math.
Następnie dowiedz się, jak pracować z defaultdict w Pythonie.
