วิธีการดำเนินการส่วนพื้นใน Python
เผยแพร่แล้ว: 2022-11-02ในบทช่วยสอนนี้ คุณจะได้เรียนรู้วิธีดำเนินการแบ่งพื้นใน Python คุณจะใช้ตัวดำเนินการ // ของ Python ฟังก์ชัน floor จากโมดูลคณิตศาสตร์ของ Python และอื่นๆ พร้อมตัวอย่างโค้ด
เราจะเริ่มต้นด้วยภาพรวมของตัวดำเนินการเลขคณิตใน Python และเรียนรู้วิธีการทำงานของตัวดำเนินการหารพื้น // จากนั้น เราจะเรียนรู้วิธีการใช้วิธีการอื่นๆ ที่เทียบเท่ากัน รวมถึงฟังก์ชันจากโมดูลคณิตศาสตร์และตัวดำเนินการเพื่อดำเนินการแบ่งพื้น
มาเริ่มกันเลย…
ตัวดำเนินการเลขคณิตใน Python
ใน Python คุณสามารถใช้ตัวดำเนินการเลขคณิตเพื่อดำเนินการทางคณิตศาสตร์อย่างง่ายกับตัวเลขประเภทข้อมูล int และ float ตัวดำเนินการเหล่านี้ดำเนินการกับตัวถูกดำเนินการ (ตัวเลข) และส่งคืนผลลัพธ์ของการดำเนินการ

ตารางต่อไปนี้สรุปตัวดำเนินการเลขคณิตใน Python และวิธีการทำงาน:
| โอเปอเรเตอร์ | ไวยากรณ์ | ผลลัพธ์ |
| บวก (+) | num1+num2 | ส่งกลับผลรวมของ num1 และ num2 |
| การลบ (-) | num1-num2 | ส่งกลับค่าความแตกต่างระหว่าง num1 และ num2 |
| การคูณ (*) | num1*num2 | ส่งกลับผลคูณของ num1 และ num2 |
| การยกกำลัง (**) | num1**num2 | ส่งกลับผลลัพธ์ของ num1 ยกกำลัง num2 ; num1 num2 |
| แผนก (/) | num1/num2 | ส่งกลับผลลัพธ์เมื่อ num1 ถูกหารด้วย num2 – รวมทั้งเศษส่วนด้วย |
| แบ่งชั้น (/) | num1//num2 | ส่งกลับผลหารเมื่อ num1 ถูกหารด้วย num2 |
| โมดูโล (%) | num1 % num2 | ส่งคืนค่าที่เหลือเมื่อ num1 หารด้วย num2 |
ลองมาดูตัวอย่างที่ใช้ตัวดำเนินการเลขคณิตเหล่านี้กัน คุณสามารถลองใช้ตัวอย่างเหล่านี้ได้ใน Python REPL หรือในตัวแก้ไข Python ออนไลน์ของ Geekflare
>>> num1 = 18 >>> num2 = 5 >>> num1 + num2 23 >>> num1 - num2 13 >>> num1 * num2 90 >>> num1 ** num2 1889568 ในตัวอย่างนี้ num1 คือ 18 และ num2 คือ 5 การดำเนินการหาร num1/num2 จะส่งกลับผลลัพธ์รวมถึงส่วนที่เป็นเศษส่วน
เลข 5 หาร 18 ได้สามครั้ง เหลือเศษสาม ดังนั้น การดำเนินการแบ่งพื้น num1//num2 ให้ผลหาร 3 ในขณะที่โอเปอเรเตอร์โมดูโลให้ส่วนที่เหลือ – เช่นกัน 3 ในกรณีนี้
>>> num1/num2 3.6 >>> num1//num2 3 >>> num1 % num2 3สิ่งนี้ควรให้แนวคิดแก่คุณเกี่ยวกับวิธีการทำงานของผู้ควบคุมการแบ่งส่วน การแบ่งพื้น และโมดูโล ต่อไป เราจะเรียนรู้เกี่ยวกับตัวดำเนินการแบ่งพื้นโดยละเอียด
️ ใน Python 2 การดำเนินการหาร (/) จะตัดผลลัพธ์ให้เป็นจำนวนเต็มที่ใกล้เคียงที่สุด—คล้ายกับการดำเนินการหารพื้นใน Python 3 บทช่วยสอนนี้จะกล่าวถึงวิธีการทำงานของการแบ่งพื้นใน Python 3.x
การแบ่งชั้นโดยใช้ // Operator

พิจารณาการดำเนินการหารด้วยเงินปันผลและตัวหาร ใน num1/num2 , num1 คือเงินปันผล และ num2 เป็นตัวหาร ในการแบ่งชั้นของ num1 และ num2 ให้ใช้ num1//num2
ตัว ดำเนินการหารพื้น (//) ส่งคืนผลหารของการดำเนินการหาร—เป็นจำนวนเต็มหรือเลขทศนิยม—ขึ้นอยู่กับชนิดข้อมูลของตัวถูกดำเนินการ
ตัวดำเนินการแบ่งพื้นไม่รับรองว่าคำตอบจะเป็นจำนวนเต็มเสมอ หากเงินปันผล ( num1 ) หรือตัวหาร ( num2 ) เป็นทศนิยม ผลลัพธ์ของ num1//num2 จะเป็นทศนิยม นี่คือตัวอย่างบางส่วน
>>> 18.0//5 3.0 >>> 10.0//4 2.0 >>> 15//4.0 3.0 หากคุณต้องการให้ผลลัพธ์เป็นจำนวนเต็ม คุณต้องแปลงเป็นจำนวนเต็มอย่างชัดเจนโดยใช้ int()
>>> int(18.0//5) 3 >>> int(10.0//4) 2 >>> int(15//4.0) 3เกิดอะไรขึ้นภายใต้ประทุน?
เมื่อคุณใช้ตัวดำเนินการแบ่งพื้น // วิธีการพิเศษ (หรือที่เรียกว่าวิธี dunder) __floordiv__() จะถูกเรียก ดังนั้น คุณยังสามารถใช้ __floordiv__() กับจำนวนเต็มหรือเลขทศนิยมใดก็ได้ ดังที่แสดงด้านล่าง:
num1 = 18 num2 = 5 num1.__floordiv__(num2) # Output: 3การแบ่งชั้นโดยใช้ตัวดำเนินการ.floordiv()

ในการดำเนินการแบ่งพื้นใน Python คุณยังสามารถใช้ floordiv() ในโมดูล operator
โมดูลตัวดำเนินการของ Python มีคำจำกัดความของฟังก์ชันที่มีประสิทธิภาพซึ่งสามารถดำเนินการทางคณิตศาสตร์ทั้งหมดได้ ดังนั้น ในการแบ่งส่วนพื้น คุณสามารถใช้ floordiv() จากโมดูลตัวดำเนินการ แทนตัวดำเนินการ //
การใช้ floordiv() จากโมดูลตัวดำเนินการจะเทียบเท่ากับการใช้ตัวดำเนินการการแบ่งพื้น
>>> import operator >>> operator.floordiv(18,5) # Output: 3 >>> operator.floordiv(12,5.0) # Output: 2.0การแบ่งชั้นโดยใช้ math.floor()
ฟังก์ชั่นพื้นทำงานอย่างไร?
ในวิชาคณิตศาสตร์ ฟังก์ชัน
floor()ใช้จำนวนจริงxใดๆ เป็นอินพุตและส่งกลับจำนวนเต็ม (ผลลัพธ์) ผลลัพธ์นี้เป็น จำนวนเต็มที่มากที่สุด ที่ น้อยกว่าหรือเท่ากับ จำนวนจริง x
เพื่อให้เข้าใจได้ดีขึ้น ให้เรายกตัวอย่างสองสามตัวอย่างและนึกภาพตัวเลขเหล่านี้บนเส้นจำนวน
ตัวอย่างที่ 1 : พิจารณาหมายเลข 2.3 จำนวนเต็มที่มากที่สุดที่น้อยกว่าหรือเท่ากับ 2.3 คือ 2; ดังนั้น floor(2.3) จะกลับมา 2
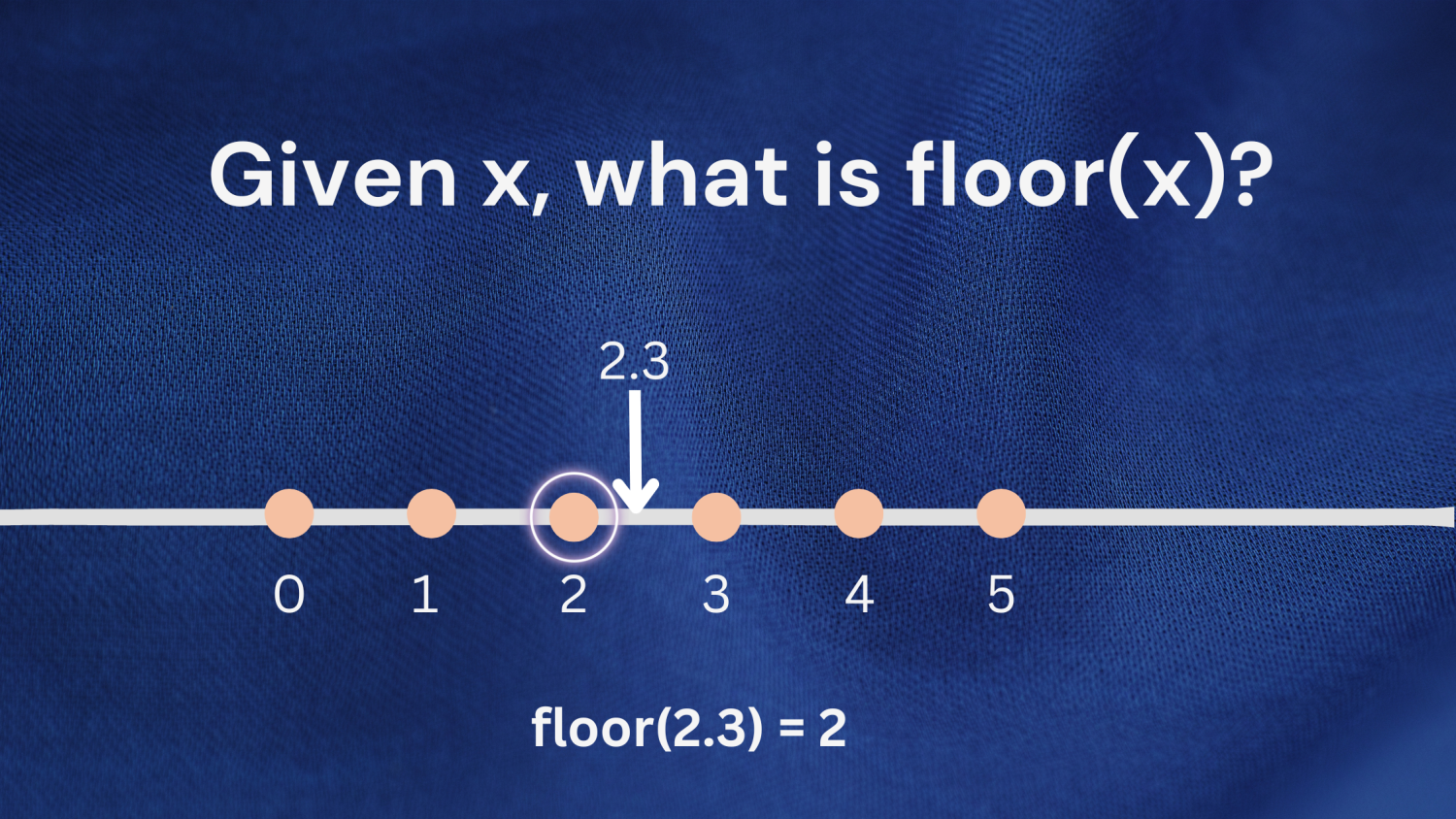
ตัวอย่าง ที่ 2: คุณสามารถใช้คำจำกัดความเดียวกันนี้เมื่อทำงานกับตัวเลขติดลบได้เช่นกัน พิจารณาตัวเลข -1.7 จำนวนเต็มที่มากที่สุดที่น้อยกว่าหรือเท่ากับ -1.7 คือ -2; ดังนั้น floor(-1.7) จะกลับมา -2

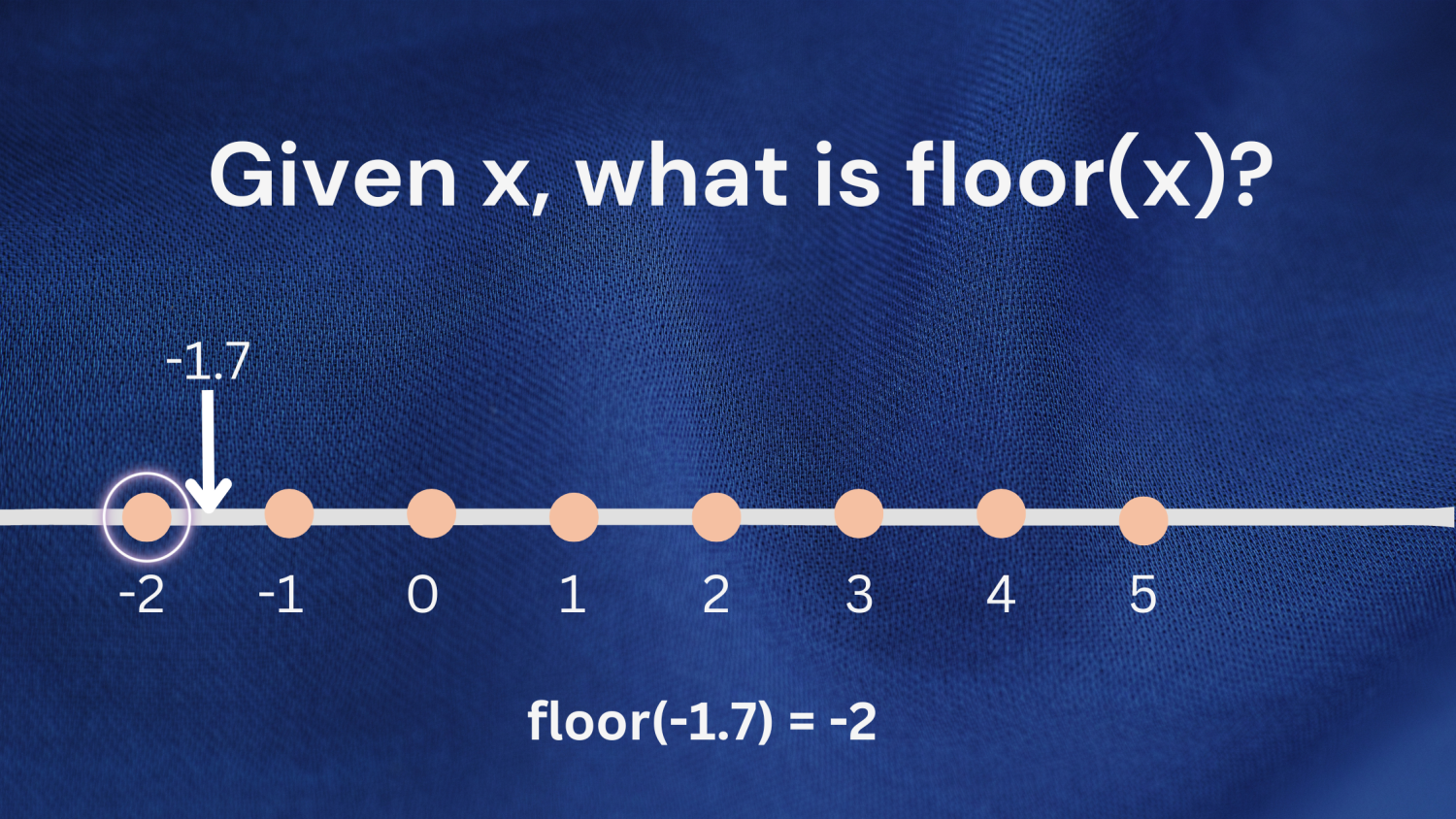
มาตรวจสอบผลลัพธ์ข้างต้นโดยใช้ฟังก์ชัน floor() จากโมดูลคณิตศาสตร์
>>> from math import floor >>> floor(2.3) 2 >>> floor(-1.7) -2 ในการแบ่งชั้น คุณสามารถเรียกใช้ฟังก์ชัน floor() โดยใช้ num1/num2 เป็นอาร์กิวเมนต์ เมื่อตัดทอนหรือปัดเศษผลลัพธ์ให้เป็นจำนวนเต็มที่ใกล้เคียงที่สุด จะเทียบเท่ากับการดำเนินการหารพื้น
คุณสามารถนำเข้าฟังก์ชัน floor() ได้อย่างชัดเจนจากโมดูล math ดังที่แสดง:
from math import floor num1 = 18 num2 = 5 floor(num1/num2) # Output: 3 หรือคุณสามารถนำเข้าเฉพาะโมดูล math แล้วเข้าถึงฟังก์ชัน floor() โดยใช้ math.floor()
import math num1 = 18 num2 = 5 math.floor(num1/num2) # Output: 3 ต่างจาก floordiv() จากโมดูลตัวดำเนินการและตัวดำเนินการส่วนพื้น // การใช้ math.floor(num1/num2) จะทำให้แน่ใจว่าผลลัพธ์เป็นจำนวนเต็ม วิธีนี้ทำให้โค้ดอ่านได้และขจัดขั้นตอนการส่งแบบพิมพ์
import math num1 = 18.0 num2 = 5 math.floor(num1/num2) # Output: 3ตัวอย่างการแบ่งชั้นใน Python

มาสรุปการสนทนาของเราด้วยตัวอย่างที่ใช้งานได้จริง: การค้นหาแบบไบนารี
การค้นหาแบบไบนารีเป็นอัลกอริธึมการค้นหาที่มีประสิทธิภาพที่ช่วยให้คุณสามารถค้นหาองค์ประกอบเป้าหมายผ่านอาร์เรย์ที่เรียงลำดับในเวลา O (บันทึก n) โดยที่ n คือขนาดของอาร์เรย์
อัลกอริทึมนี้ทำงานโดยแบ่งช่วงการค้นหาออกเป็นครึ่งหนึ่งในแต่ละขั้นตอน ซึ่งทำได้โดยขึ้นอยู่กับว่าจุดกึ่งกลางของช่วงนั้นตรงกับเป้าหมายหรือไม่ (การค้นหาสิ้นสุดลงเมื่อพบว่าตรงกัน!) หรือน้อยกว่าหรือมากกว่าเป้าหมาย เนื่องจากขนาดของอาร์เรย์ลดลงครึ่งหนึ่งในแต่ละขั้นตอน จุดกึ่งกลางจึงไม่ได้ประเมินเป็นจำนวนเต็มเสมอไป
itemlist = [5,7,18,21,34,45] item = 7 พิจารณาการใช้งานอัลกอริธึมการค้นหาแบบไบนารีต่อไปนี้ ฟังก์ชัน binary_search() ใช้ตัวเลข ( item ) และ list ( itemlist ) และค้นหา item ใน itemlist
- หากพบ
itemฟังก์ชันจะส่งกลับดัชนีที่เกิดitem - มิฉะนั้นจะส่งคืน
None
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use normal division instead of floor division midPt = (lowerIdx + upperIdx)/ 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return None การใช้งานนี้ถูกต้องตามหน้าที่ ยกเว้นว่าเรายังไม่ได้พิจารณา midPt ที่ไม่ได้ประเมินเป็นจำนวนเต็มในขณะที่การค้นหาดำเนินการ
binary_search(item,itemlist) หากเราเรียกใช้ฟังก์ชัน เราจะพบ TypeError โดยระบุว่าดัชนีรายการต้องเป็นจำนวนเต็มหรือสไลซ์ ไม่ใช่ลอย
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-3-a5f12ebc3145> in <module> ----> 1 binary_search(item,itemlist) <ipython-input-2-524ef6900b1f> in binary_search(item, itemlist) 12 13 # if item is found, return the index ---> 14 if itemlist[midPt] == item: 15 return midPt 16 # otherwise get the next midpoint TypeError: list indices must be integers or slices, not floatเราแก้ไขนิยามฟังก์ชันเพื่อใช้ตัวดำเนินการแบ่งพื้น:
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use floor division midPt = (lowerIdx + upperIdx)// 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return Noneฟังก์ชันส่งคืนดัชนีที่พบรายการ 7 ซึ่งเป็นดัชนีหนึ่ง
binary_search(item,itemlist) # Output: 1บทสรุป
ฉันหวังว่าบทช่วยสอนนี้จะช่วยให้คุณเข้าใจวิธีการแบ่งส่วนพื้นใน Python นี่คือบทสรุปของวิธีการต่างๆ ที่คุณได้เรียนรู้:
- ใน Python ตัวดำเนินการ b ดำเนินการตามที่กำหนดโดยตัวดำเนินการ โดยมี a และ b เป็นตัวถูกดำเนินการและส่งกลับผลลัพธ์ของการดำเนินการ
- คุณสามารถใช้ตัวดำเนินการหารพื้นของ Python //; a//b ส่งกลับผลหารของการดำเนินการหาร a/b
- หรือคุณสามารถใช้ ฟังก์ชัน floordiv() ที่เทียบเท่าที่กำหนดไว้ในโมดูลตัวดำเนินการของ Python ด้วยไวยากรณ์: operator.floordiv(a,b) เพื่อรับผลลัพธ์ของ a//b
- เมธอดทั้งหมดข้างต้นส่งคืนผลหาร แต่ชนิดข้อมูลอาจเป็นแบบทศนิยมหรือแบบ int ขึ้นอยู่กับค่าของ a และ b ดังนั้นคุณจะต้องแปลงค่าที่ส่งคืนเป็นจำนวนเต็ม
- ฟังก์ชัน floor() จากโมดูลคณิตศาสตร์ของ Python สามารถใช้ในการแบ่งชั้นได้: math.floor(a,b) เทียบเท่ากับ a//b และคืนค่าเป็นจำนวนเต็ม เมื่อคุณต้องการให้ผลลัพธ์เป็นจำนวนเต็ม ให้พิจารณาใช้ฟังก์ชันพื้นจากโมดูลคณิตศาสตร์
ต่อไป เรียนรู้วิธีการทำงานกับ defaultdict ใน Python
