Comment effectuer la division du sol en Python
Publié: 2022-11-02Dans ce didacticiel, vous apprendrez à effectuer une division d'étage en Python. Vous utiliserez l'opérateur // de Python, la fonction floor du module mathématique de Python, et plus encore, avec des exemples de code.
Nous commencerons par un aperçu des opérateurs arithmétiques en Python et apprendrons comment fonctionne l'opérateur de division de plancher //. Ensuite, nous apprendrons à utiliser d'autres méthodes équivalentes, y compris les fonctions des modules mathématiques et opérateur, pour effectuer la division d'étage.
Commençons…
Opérateurs arithmétiques en Python
En Python, vous pouvez utiliser des opérateurs arithmétiques pour effectuer des opérations arithmétiques simples sur des nombres de types int et float . Ces opérateurs agissent sur des opérandes (les nombres) et renvoient le résultat de l'opération.

Le tableau suivant résume les opérateurs arithmétiques en Python et leur fonctionnement :
| Opérateur | Syntaxe | Résultat |
| Ajout (+) | num1+num2 | Renvoie la somme de num1 et num2 |
| Soustraction (-) | num1-num2 | Renvoie la différence entre num1 et num2 |
| Multiplication (*) | num1*num2 | Renvoie le produit de num1 et num2 |
| Exponentation (**) | num1**num2 | Renvoie le résultat de num1 élevé à la puissance de num2 ; num1 num2 |
| Section (/) | num1/num2 | Renvoie le résultat lorsque num1 est divisé par num2 - y compris la partie fractionnaire |
| Répartition au sol (/) | num1//num2 | Renvoie le quotient lorsque num1 est divisé par num2 |
| Module (%) | num1 % num2 | Renvoie le reste lorsque num1 est divisé par num2 |
Prenons quelques exemples qui utilisent ces opérateurs arithmétiques. Vous pouvez essayer ces exemples dans un REPL Python ou dans l'éditeur Python en ligne de Geekflare.
>>> num1 = 18 >>> num2 = 5 >>> num1 + num2 23 >>> num1 - num2 13 >>> num1 * num2 90 >>> num1 ** num2 1889568 Dans cet exemple, num1 est 18 et num2 est 5. L'opération de division num1/num2 renvoie le résultat, y compris la partie fractionnaire.
Le nombre 5 va dans 18 trois fois laissant un reste de trois. Par conséquent, l'opération de division du plancher, num1//num2 , donne le quotient 3, tandis que l'opérateur modulo donne le reste - également 3 dans ce cas.
>>> num1/num2 3.6 >>> num1//num2 3 >>> num1 % num2 3Cela devrait vous donner une idée du fonctionnement des opérateurs de division, de division d'étage et de modulo. Ensuite, nous découvrirons en détail l'opérateur de division d'étage.
️ Dans Python 2, l'opération de division (/) tronque le résultat à l'entier le plus proche, similaire à l'opération de division de plancher dans Python 3. Ce didacticiel explique comment fonctionne l'opération de division de plancher dans Python 3.x.
Division d'étage à l'aide de l'opérateur //

Considérons une opération de division avec un dividende et un diviseur. Dans num1/num2 , num1 est le dividende et num2 est le diviseur. Pour effectuer la division par étage de num1 et num2 , utilisez num1//num2 .
L' opérateur de division d'étage (//) renvoie le quotient de l'opération de division, sous forme d'entier ou de nombre à virgule flottante, selon les types de données des opérandes.
L'opérateur de division d'étage ne garantit pas que la réponse est toujours un nombre entier. Si le dividende ( num1 ) ou le diviseur ( num2 ) est un flottant, alors le résultat de num1//num2 est un flottant. Voici quelques exemples.
>>> 18.0//5 3.0 >>> 10.0//4 2.0 >>> 15//4.0 3.0 Si vous avez besoin que le résultat soit un entier, vous devez le convertir explicitement en un entier à l'aide de la fonction int() :
>>> int(18.0//5) 3 >>> int(10.0//4) 2 >>> int(15//4.0) 3Que se passe-t-il sous le capot ?
Lorsque vous utilisez l'opérateur de division d'étage //, la méthode spéciale (également appelée méthode dunder) __floordiv__() est appelée. Par conséquent, vous pouvez également utiliser la __floordiv__() sur n'importe quel entier ou nombre à virgule flottante, comme indiqué ci-dessous :
num1 = 18 num2 = 5 num1.__floordiv__(num2) # Output: 3Division d'étage à l'aide de operator.floordiv()

Pour effectuer une division d'étage en Python, vous pouvez également utiliser la fonction floordiv() dans le module operator .
Le module opérateur de Python contient les définitions de fonctions efficaces qui peuvent effectuer toutes les opérations arithmétiques. Par conséquent, pour effectuer une division d'étage, vous pouvez également utiliser la fonction floordiv() du module opérateur - au lieu de l'opérateur //.
L'utilisation de la fonction floordiv() du module opérateur équivaut à l'utilisation de l'opérateur de division d'étage.
>>> import operator >>> operator.floordiv(18,5) # Output: 3 >>> operator.floordiv(12,5.0) # Output: 2.0Division du sol à l'aide de math.floor()
Comment fonctionne la fonction Floor ?
En mathématiques, la fonction
floor()prend n'importe quel nombre réelxcomme entrée et renvoie un entier (résultat). Ce résultat est le plus grand entier inférieur ou égal au nombre réel x.
Pour mieux comprendre cela, prenons quelques exemples et visualisons ces nombres sur une droite numérique.
Exemple 1 : Considérons le nombre 2.3. Le plus grand entier inférieur ou égal à 2,3 est 2 ; donc floor(2.3) renverra 2.

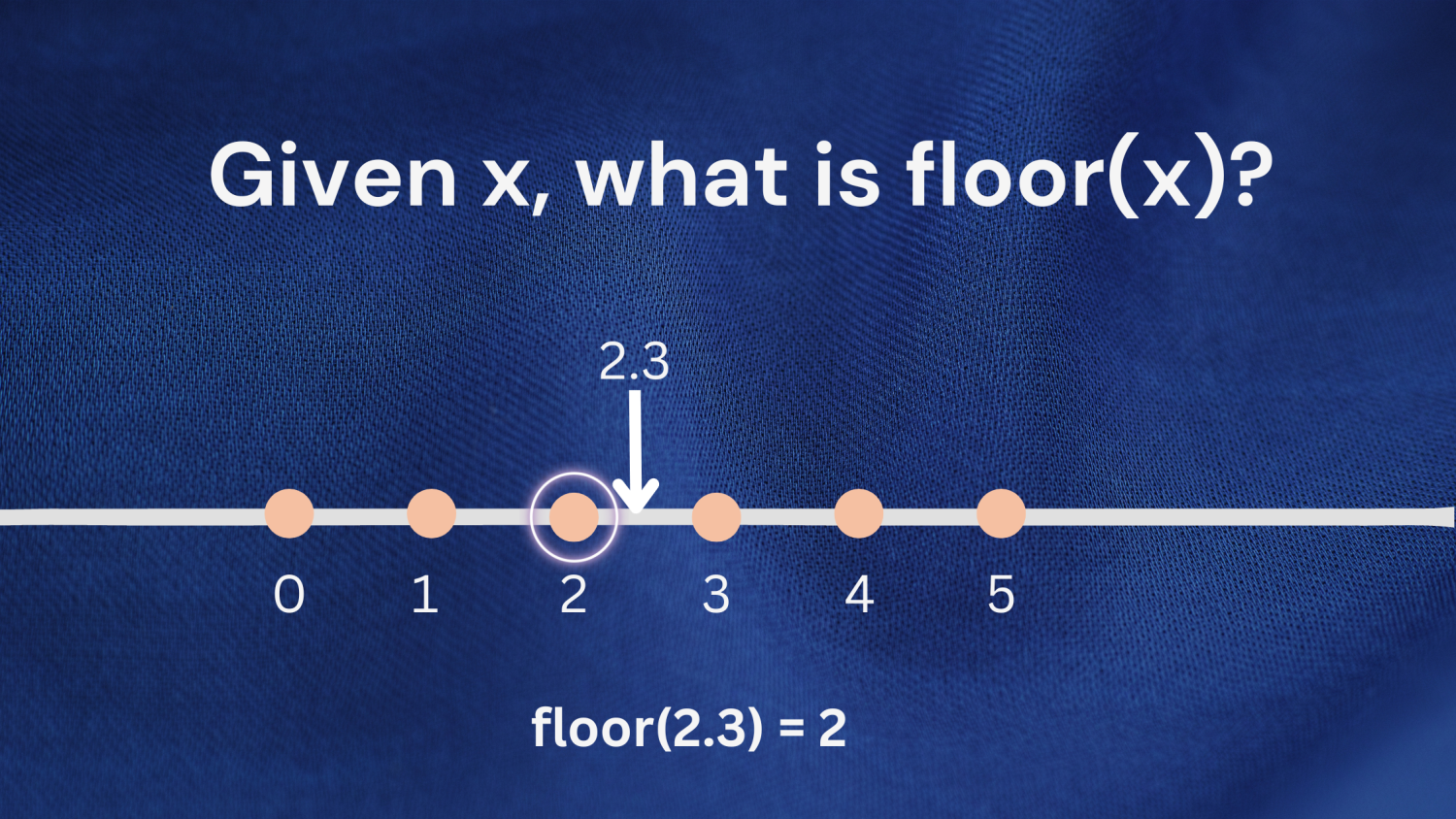
Exemple 2 : Vous pouvez également appliquer la même définition lorsque vous travaillez avec des nombres négatifs. Considérez le nombre -1,7. Le plus grand entier inférieur ou égal à -1,7 est -2 ; donc floor(-1.7) renverra -2.
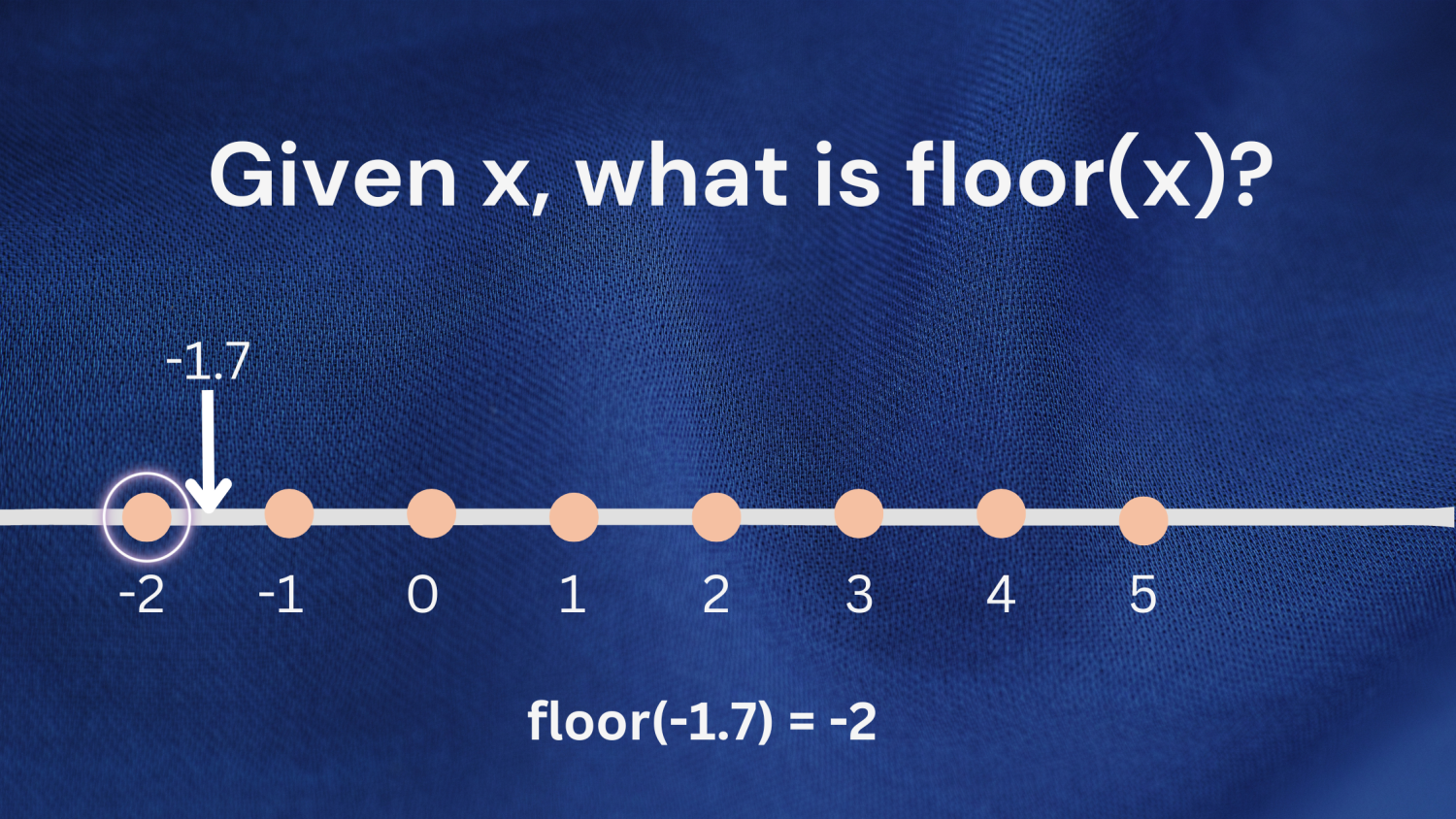
Vérifions les résultats ci-dessus en utilisant la fonction floor() du module math.
>>> from math import floor >>> floor(2.3) 2 >>> floor(-1.7) -2 Pour effectuer une division d'étage, vous pouvez appeler la fonction floor() avec num1/num2 comme argument. Comme il tronque ou arrondit le résultat à l'entier le plus proche, cela équivaut à l'opération de division du plancher.
Vous pouvez explicitement importer la fonction floor() du module math , comme indiqué :
from math import floor num1 = 18 num2 = 5 floor(num1/num2) # Output: 3 Alternativement, vous pouvez également importer uniquement le module math , puis accéder à la fonction floor() en utilisant math.floor() .
import math num1 = 18 num2 = 5 math.floor(num1/num2) # Output: 3 Contrairement à la fonction floordiv() du module opérateur et à l'opérateur de division d'étage //, l'utilisation math.floor(num1/num2) garantit que le résultat est un entier. Cette méthode rend le code lisible et élimine l'étape de transtypage.
import math num1 = 18.0 num2 = 5 math.floor(num1/num2) # Output: 3Exemples de division d'étage en Python

Terminons notre discussion par un exemple pratique : la recherche binaire.
La recherche binaire est un algorithme de recherche efficace qui vous permet de rechercher un élément cible dans des tableaux triés en un temps O(log n) , où n est la taille du tableau.
Cet algorithme fonctionne en divisant l'intervalle de recherche en deux à chaque étape. Cela se fait selon que le milieu de l'intervalle correspond à la cible (la recherche se termine dès qu'une correspondance est trouvée !) ou est inférieur ou supérieur à la cible. Comme la taille du tableau est réduite de moitié à chaque étape, le point médian n'est pas toujours évalué à un entier.
itemlist = [5,7,18,21,34,45] item = 7 Considérez l'implémentation suivante de l'algorithme de recherche binaire. La fonction binary_search() prend un nombre ( item ) et une liste ( itemlist ) et recherche l'occurrence de l' item dans itemlist .
- Si l'
itemest trouvé, la fonction renvoie l'index auquelitemapparaît. - Sinon, il renvoie
None.
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use normal division instead of floor division midPt = (lowerIdx + upperIdx)/ 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return None Cette implémentation est fonctionnellement correcte, sauf que nous n'avons pas pris en compte le fait que le midPt ne s'évalue pas en entier au fur et à mesure que la recherche progresse.
binary_search(item,itemlist) Si nous appelons la fonction, nous rencontrons une TypeError indiquant que les indices de la liste doivent être des entiers ou des tranches, et non flottants.
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-3-a5f12ebc3145> in <module> ----> 1 binary_search(item,itemlist) <ipython-input-2-524ef6900b1f> in binary_search(item, itemlist) 12 13 # if item is found, return the index ---> 14 if itemlist[midPt] == item: 15 return midPt 16 # otherwise get the next midpoint TypeError: list indices must be integers or slices, not floatNous modifions la définition de la fonction pour utiliser l'opérateur de division d'étage :
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use floor division midPt = (lowerIdx + upperIdx)// 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return NoneLa fonction renvoie l'index auquel se trouve l'élément 7, qui est l'index un.
binary_search(item,itemlist) # Output: 1Conclusion
J'espère que ce tutoriel vous a aidé à comprendre comment effectuer la division du sol en Python. Voici un résumé des différentes méthodes que vous avez apprises :
- En Python, un opérateur b effectue l'opération définie par l'opérateur avec a et b comme opérandes et renvoie le résultat de l'opération.
- Vous pouvez utiliser l'opérateur de division d'étage de Python //; a//b renvoie le quotient de l'opération de division a/b.
- Alternativement, vous pouvez utiliser la fonction équivalente floordiv() définie dans le module opérateur de Python avec la syntaxe : operator.floordiv(a,b) pour obtenir le résultat de a//b.
- Toutes les méthodes ci-dessus renvoient le quotient mais le type de données peut être un float ou un int selon les valeurs de a et b. Vous devrez donc convertir la valeur de retour en un entier.
- La fonction floor() du module mathématique de Python peut également être utilisée pour effectuer une division d'étage : math.floor(a,b) équivaut à a//b et renvoie un entier. Lorsque vous voulez que le résultat soit un entier, envisagez d'utiliser la fonction floor du module mathématique.
Ensuite, apprenez à travailler avec defaultdict en Python.
