Python でフロア除算を実行する方法
公開: 2022-11-02このチュートリアルでは、Python でフロア分割を実行する方法を学習します。 コード例とともに、Python の // 演算子、Python の math モジュールの floor 関数などを使用します。
Python の算術演算子の概要から始め、床除算演算子 // がどのように機能するかを学びます。 次に、math および operator モジュールの関数を含む他の同等のメソッドを使用して、フロア除算を実行する方法を学習します。
始めましょう…
Python の算術演算子
Python では、算術演算子を使用して、 intおよびfloatデータ型の数値に対して単純な算術演算を実行できます。 これらの演算子はオペランド (数値) に作用し、演算の結果を返します。

次の表は、Python の算術演算子とその動作をまとめたものです。
| オペレーター | 構文 | 結果 |
| 加算 (+) | num1+num2 | num1とnum2の合計を返します |
| 減算 (-) | num1-num2 | num1とnum2の差を返します |
| 乗算 (*) | num1*num2 | num1とnum2の積を返します |
| べき乗 (**) | num1**num2 | num1をnum2で累乗した結果を返します。 num1 num2 |
| 分割 (/) | num1/num2 | num1をnum2で除算した結果を返します (小数部分を含む) |
| フロア区分 (/) | num1//num2 | num1をnum2で割ったときの商を返します。 |
| モジュロ (%) | num1 % num2 | num1をnum2で割った余りを返します。 |
これらの算術演算子を使用する例をいくつか見てみましょう。 これらの例は、Python REPL または Geekflare のオンライン Python エディターで試すことができます。
>>> num1 = 18 >>> num2 = 5 >>> num1 + num2 23 >>> num1 - num2 13 >>> num1 * num2 90 >>> num1 ** num2 1889568 この例では、 num1は 18 で、 num2は 5 です。除算num1/num2は、小数部分を含む結果を返します。
5 は 18 に 3 回入り、残りは 3 です。 したがって、階除算演算num1//num2は商 3 を返し、モジュロ演算子は剰余を返します。この場合も 3 です。
>>> num1/num2 3.6 >>> num1//num2 3 >>> num1 % num2 3これにより、除算、フロア除算、モジュロ演算子がどのように機能するかがわかります。 次に、フロア除算演算子について詳しく学習します。
️ Python 2 では、除算演算 (/) は結果を最も近い整数に切り捨てます—Python 3 の床除算演算と同様です。このチュートリアルでは、Python 3.x で床除算演算がどのように機能するかについて説明します。
// 演算子を使用したフロア分割

被除数と除数による除算を考えてみましょう。 num1/num2では、 num1は被除数、 num2は除数です。 num1とnum2のフロア除算を実行するには、 num1//num2を使用します。
階除算演算子(//) は、オペランドのデータ型に応じて、除算の商を整数または浮動小数点数として返します。
フロア除算演算子は、答えが常に整数であることを保証しません。 被除数 ( num1 ) または除数 ( num2 ) が float の場合、 num1//num2の結果は float です。 いくつかの例を次に示します。
>>> 18.0//5 3.0 >>> 10.0//4 2.0 >>> 15//4.0 3.0 結果を整数にする必要がある場合は、 int()関数を使用して明示的に整数にキャストする必要があります。
>>> int(18.0//5) 3 >>> int(10.0//4) 2 >>> int(15//4.0) 3ボンネットの下で何が起こるか?
床除算演算子 // を使用すると、特別なメソッド (dunder メソッドとも呼ばれます) __floordiv__()が呼び出されます。 したがって、以下に示すように、任意の整数または浮動小数点数で__floordiv__()メソッドを使用することもできます。
num1 = 18 num2 = 5 num1.__floordiv__(num2) # Output: 3operator.floordiv() を使用したフロア分割

Python でフロア除算を実行するには、 operatorモジュールでfloordiv()関数を使用することもできます。
Python の operator モジュールには、すべての算術演算を実行できる効率的な関数の定義が含まれています。 したがって、フロア除算を実行するには、// 演算子の代わりに operator モジュールのfloordiv()関数を使用することもできます。
operator モジュールからfloordiv()関数を使用することは、フロア除算演算子を使用することと同じです。
>>> import operator >>> operator.floordiv(18,5) # Output: 3 >>> operator.floordiv(12,5.0) # Output: 2.0math.floor() を使用した床割り
フロア機能はどのように機能しますか?
数学では、
floor()関数は任意の実数xを入力として受け取り、整数 (結果) を返します。 この結果は、実数 x以下の最大の整数です。
これをよりよく理解するために、いくつかの例を挙げて、これらの数値を数直線で視覚化してみましょう。
例 1 : 数値 2.3 を考えてみましょう。 2.3 以下の最大の整数は 2 です。 したがって、floor(2.3) は 2 を返します。
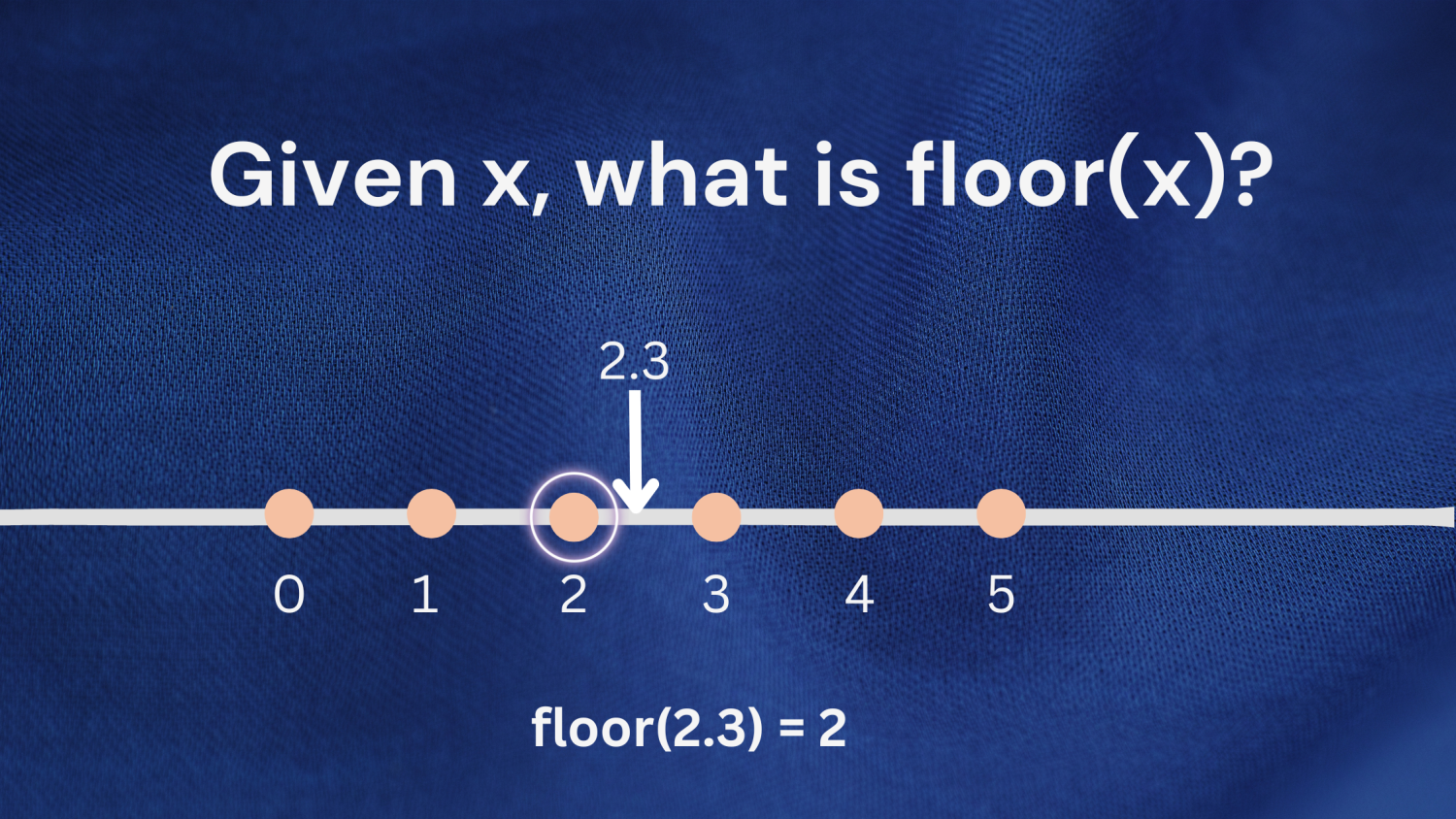
例2: 負の数を扱う場合にも同じ定義を適用できます。 数 -1.7 を考えてみましょう。 -1.7 以下の最大の整数は -2 です。 したがって、floor(-1.7) は -2 を返します。

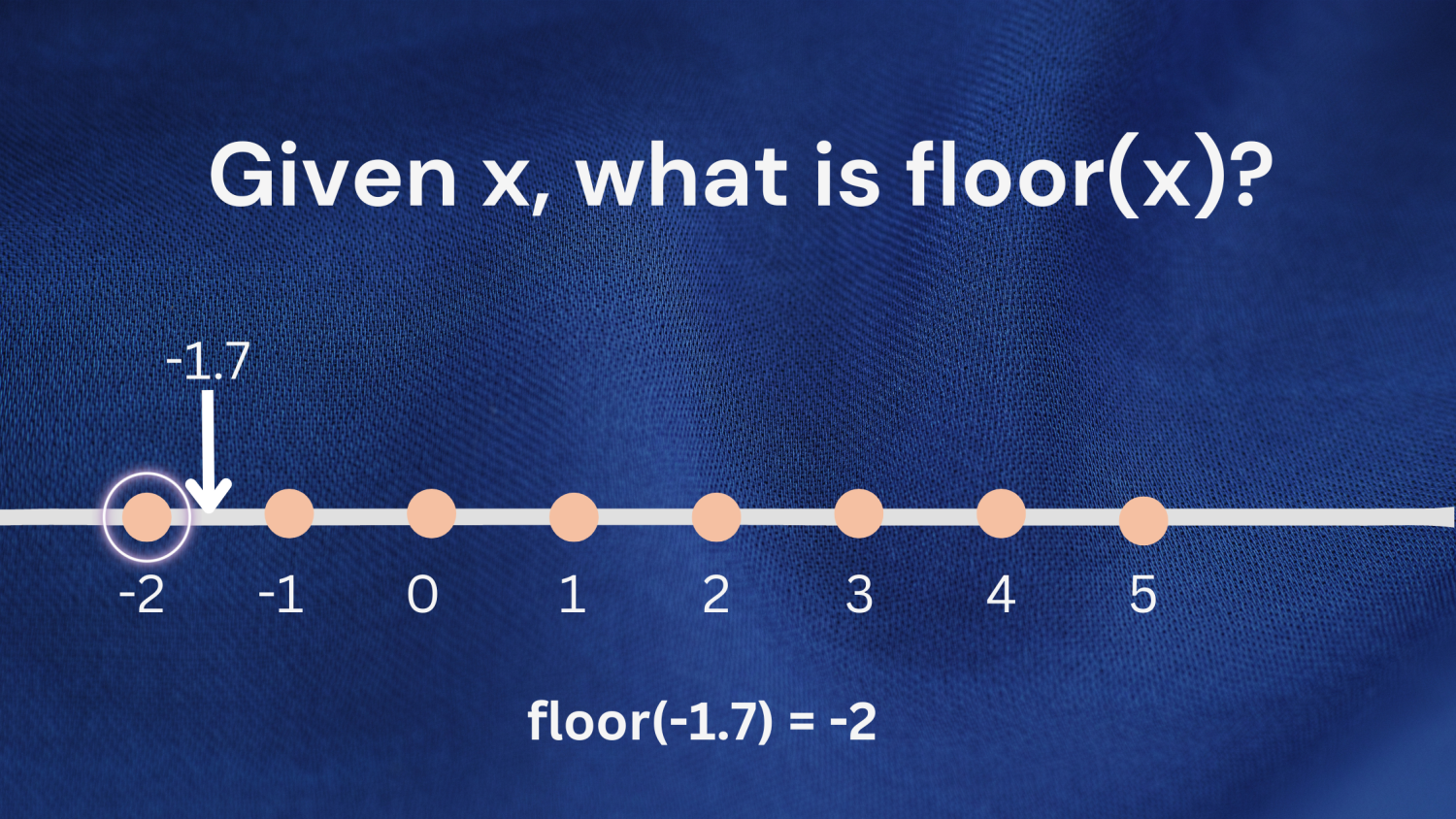
math モジュールのfloor()関数を使用して、上記の結果を確認してみましょう。
>>> from math import floor >>> floor(2.3) 2 >>> floor(-1.7) -2 フロア除算を実行するには、引数としてnum1/num2を指定してfloor()関数を呼び出すことができます。 結果を最も近い整数に切り捨てるか、切り捨てるため、床除算演算と同等です。
次のように、 mathモジュールからfloor()関数を明示的にインポートできます。
from math import floor num1 = 18 num2 = 5 floor(num1/num2) # Output: 3 または、 mathモジュールのみをインポートしてから、 math.floor()を使用してfloor()関数にアクセスすることもできます。
import math num1 = 18 num2 = 5 math.floor(num1/num2) # Output: 3 operator モジュールのfloordiv()関数およびフロア除算演算子 // とは異なり、math.floor math.floor(num1/num2)を使用すると、結果が確実に整数になります。 この方法により、コードが読みやすくなり、型キャストの手順が不要になります。
import math num1 = 18.0 num2 = 5 math.floor(num1/num2) # Output: 3Python でのフロア分割の例

実際の例で議論を締めくくりましょう: 二分探索。
二分検索は効率的な検索アルゴリズムで、ソートされた配列からターゲット要素をO(log n)時間で検索できます。ここで、 nは配列のサイズです。
このアルゴリズムは、各ステップで検索間隔を半分に分割することによって機能します。 これは、間隔の中間点がターゲットに一致するか (一致が見つかったときに検索が終了します!)、ターゲットよりも小さいか大きいかによって行われます。 配列のサイズは各ステップで半分に縮小されるため、中点は常に整数に評価されるとは限りません。
itemlist = [5,7,18,21,34,45] item = 7 二分探索アルゴリズムの次の実装を検討してください。 関数binary_search()は、数値 ( item ) とリスト ( itemlist ) を受け取り、 itemlist内のitemの出現を検索します。
-
itemが見つかった場合、関数はitemが出現するインデックスを返します。 - それ以外の場合は
Noneを返します。
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use normal division instead of floor division midPt = (lowerIdx + upperIdx)/ 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return None この実装は、検索が進むにつれてmidPtが整数に評価されないことを考慮していないことを除いて、機能的に正しいです。
binary_search(item,itemlist) 関数を呼び出すと、リストのインデックスは float ではなく整数またはスライスでなければならないことを示すTypeErrorが発生します。
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-3-a5f12ebc3145> in <module> ----> 1 binary_search(item,itemlist) <ipython-input-2-524ef6900b1f> in binary_search(item, itemlist) 12 13 # if item is found, return the index ---> 14 if itemlist[midPt] == item: 15 return midPt 16 # otherwise get the next midpoint TypeError: list indices must be integers or slices, not floatフロア除算演算子を使用するように関数定義を変更します。
def binary_search(item, itemlist): # get the list size listsize = len(itemlist) - 1 # start at the two ends of the list lowerIdx = 0 upperIdx = listsize while lowerIdx <= upperIdx: # calculate the middle point # use floor division midPt = (lowerIdx + upperIdx)// 2 # if item is found, return the index if itemlist[midPt] == item: return midPt # otherwise get the next midpoint if item > itemlist[midPt]: lowerIdx = midPt + 1 else: upperIdx = midPt - 1 if lowerIdx > upperIdx: return Noneこの関数は、アイテム 7 が見つかったインデックス (インデックス 1) を返します。
binary_search(item,itemlist) # Output: 1結論
このチュートリアルが、Python で床分割を実行する方法を理解するのに役立つことを願っています。 これまでに学んださまざまな方法の概要を以下に示します。
- Python では、演算子 bは、a と b をオペランドとして、演算子によって定義された演算を実行し、演算の結果を返します。
- Python の床除算演算子 //; を使用できます。 a//bは、除算 a/b の商を返します。
- または、Python の operator モジュールで定義されている同等のfloordiv()関数を構文operator.floordiv(a,b)で使用して、a//b の結果を取得することもできます。
- 上記のメソッドはすべて商を返しますが、データ型は a と b の値に応じて float または int になります。 したがって、戻り値を整数にキャストする必要があります。
- Python の math モジュールのfloor()関数を使用して、床除算を実行することもできます: math.floor(a,b)はa//bと同等で、整数を返します。 結果を整数にしたい場合は、math モジュールの floor 関数の使用を検討してください。
次に、Python で defaultdict を使用する方法を学びます。
