วิธีวิเคราะห์ข้อมูลเชิงสำรวจ (EDA) ใน R (พร้อมตัวอย่าง)
เผยแพร่แล้ว: 2022-11-11เรียนรู้ทุกสิ่งที่คุณจำเป็นต้องรู้เกี่ยวกับการวิเคราะห์ข้อมูลเชิงสำรวจ ซึ่งเป็นกระบวนการสำคัญที่ใช้ในการค้นหาแนวโน้มและรูปแบบ และสรุปชุดข้อมูลโดยใช้ข้อมูลสรุปทางสถิติและการแสดงภาพกราฟิก
เช่นเดียวกับโครงการอื่นๆ โครงการวิทยาศาสตร์ข้อมูลเป็นกระบวนการที่ยาวนานซึ่งต้องใช้เวลา การจัดระเบียบที่ดี และความเคารพอย่างถี่ถ้วนในหลายขั้นตอน การวิเคราะห์ข้อมูลเชิงสำรวจ (EDA) เป็นหนึ่งในขั้นตอนที่สำคัญที่สุดในกระบวนการนี้
ดังนั้น ในบทความนี้ เราจะมาดูสั้น ๆ ว่าการวิเคราะห์ข้อมูลเชิงสำรวจคืออะไร และคุณจะใช้งาน R!
การวิเคราะห์ข้อมูลเชิงสำรวจคืออะไร?
การวิเคราะห์ข้อมูลเชิงสำรวจจะตรวจสอบและศึกษาลักษณะของชุดข้อมูลก่อนที่จะส่งไปยังแอปพลิเคชัน ไม่ว่าจะเป็นด้านธุรกิจ สถิติ หรือแมชชีนเลิร์นนิงเท่านั้น

บทสรุปเกี่ยวกับธรรมชาติของข้อมูลและลักษณะเฉพาะหลักของข้อมูลนี้มักใช้วิธีการแสดงภาพ เช่น การนำเสนอแบบกราฟิกและตาราง การปฏิบัติจะดำเนินการล่วงหน้าอย่างแม่นยำเพื่อประเมินศักยภาพของข้อมูลเหล่านี้ ซึ่งจะได้รับการรักษาที่ซับซ้อนมากขึ้นในอนาคต
ดังนั้น EDA จึงอนุญาตให้:
- กำหนดสมมติฐานสำหรับการใช้ข้อมูลนี้
- สำรวจรายละเอียดที่ซ่อนอยู่ในโครงสร้างข้อมูล
- ระบุค่าที่หายไป ค่าผิดปกติ หรือพฤติกรรมผิดปกติ
- ค้นพบแนวโน้มและตัวแปรที่เกี่ยวข้องโดยรวม
- ละทิ้งตัวแปรที่ไม่เกี่ยวข้องหรือตัวแปรที่สัมพันธ์กับผู้อื่น
- กำหนดรูปแบบที่เป็นทางการที่จะใช้
อะไรคือความแตกต่างระหว่างการวิเคราะห์ข้อมูลเชิงพรรณนาและเชิงสำรวจ?
การวิเคราะห์ข้อมูลมีสองประเภท การวิเคราะห์เชิงพรรณนา และการวิเคราะห์ข้อมูลเชิงสำรวจ ซึ่งไปด้วยกันได้ แม้ว่าจะมีเป้าหมายต่างกัน
ในขณะที่ข้อแรกเน้นที่การอธิบายพฤติกรรมของตัวแปร เช่น ค่าเฉลี่ย ค่ามัธยฐาน โหมด ฯลฯ
การวิเคราะห์เชิงสำรวจมีจุดมุ่งหมายเพื่อระบุความสัมพันธ์ระหว่างตัวแปร ดึงข้อมูลเชิงลึกเบื้องต้น และชี้นำการสร้างแบบจำลองไปยังกระบวนทัศน์การเรียนรู้ของเครื่องทั่วไป ได้แก่ การจำแนก การถดถอย และการจัดกลุ่ม
โดยทั่วไปแล้ว ทั้งคู่อาจจัดการกับการแสดงภาพกราฟิก อย่างไรก็ตาม มีเพียงการวิเคราะห์เชิงสำรวจเท่านั้นที่พยายามนำข้อมูลเชิงลึกที่สามารถนำไปปฏิบัติได้ นั่นคือ ข้อมูลเชิงลึกที่กระตุ้นการดำเนินการโดยผู้มีอำนาจตัดสินใจ
สุดท้าย ในขณะที่การวิเคราะห์ข้อมูลเชิงสำรวจพยายามที่จะแก้ปัญหาและนำเสนอแนวทางแก้ไขที่จะเป็นแนวทางสำหรับขั้นตอนการสร้างแบบจำลอง การวิเคราะห์เชิงพรรณนาตามความหมายของชื่อนั้น มุ่งหวังที่จะสร้างคำอธิบายโดยละเอียดของชุดข้อมูลที่เป็นปัญหาเท่านั้น
| การวิเคราะห์เชิงพรรณนา | การวิเคราะห์ข้อมูลเชิงสำรวจ |
| วิเคราะห์พฤติกรรม | วิเคราะห์พฤติกรรมและความสัมพันธ์ |
| ให้ข้อมูลสรุป | นำไปสู่ข้อกำหนดและการดำเนินการ |
| จัดระเบียบข้อมูลในตารางและกราฟ | จัดระเบียบข้อมูลในตารางและกราฟ |
| ไม่มีอำนาจอธิบายที่สำคัญ | มีอำนาจอธิบายที่สำคัญ |
การใช้งานจริงบางกรณีของ EDA
#1. การตลาดดิจิทัล
การตลาดดิจิทัลได้พัฒนาจากกระบวนการสร้างสรรค์ไปสู่กระบวนการที่ขับเคลื่อนด้วยข้อมูล องค์กรการตลาดใช้การวิเคราะห์ข้อมูลเชิงสำรวจเพื่อกำหนดผลลัพธ์ของแคมเปญหรือความพยายาม และเพื่อเป็นแนวทางในการลงทุนของผู้บริโภคและการตัดสินใจกำหนดเป้าหมาย
การศึกษาทางประชากรศาสตร์ การแบ่งกลุ่มลูกค้า และเทคนิคอื่นๆ ช่วยให้นักการตลาดใช้การซื้อของผู้บริโภค การสำรวจ และข้อมูลแผงจำนวนมากเพื่อทำความเข้าใจและสื่อสารการตลาดเชิงกลยุทธ์
การวิเคราะห์เชิงสำรวจเว็บช่วยให้นักการตลาดรวบรวมข้อมูลระดับเซสชันเกี่ยวกับการโต้ตอบบนเว็บไซต์ได้ Google Analytics เป็นตัวอย่างของเครื่องมือวิเคราะห์ที่เป็นที่นิยมและฟรีซึ่งนักการตลาดใช้เพื่อจุดประสงค์นี้
เทคนิคการสำรวจที่ใช้บ่อยในการตลาด ได้แก่ การสร้างแบบจำลองส่วนประสมทางการตลาด การวิเคราะห์ราคาและการส่งเสริมการขาย การเพิ่มประสิทธิภาพการขาย และการวิเคราะห์ลูกค้าเชิงสำรวจ เช่น การแบ่งส่วน
#2. การวิเคราะห์ผลงานสำรวจ
การประยุกต์ใช้การวิเคราะห์ข้อมูลเชิงสำรวจโดยทั่วไปคือการวิเคราะห์พอร์ตโฟลิโอเชิงสำรวจ ธนาคารหรือหน่วยงานให้กู้ยืมมีบัญชีที่มีมูลค่าและความเสี่ยงต่างกัน
บัญชีอาจแตกต่างกันไปตามสถานะทางสังคมของผู้ถือ (รวย ชนชั้นกลาง คนจน ฯลฯ) ที่ตั้งทางภูมิศาสตร์ มูลค่าสุทธิ และปัจจัยอื่นๆ ผู้ให้กู้ต้องสมดุลผลตอบแทนจากเงินกู้กับความเสี่ยงในการผิดนัดเงินกู้แต่ละครั้ง คำถามจะกลายเป็นวิธีการให้ความสำคัญกับพอร์ตโฟลิโอโดยรวม
เงินกู้ที่มีความเสี่ยงต่ำที่สุดอาจมีไว้สำหรับคนที่ร่ำรวยมาก แต่ก็มีคนร่ำรวยจำนวนจำกัด ในทางกลับกัน คนยากจนจำนวนมากสามารถให้ยืมได้ แต่มีความเสี่ยงมากกว่า
โซลูชันการวิเคราะห์ข้อมูลเชิงสำรวจสามารถรวมการวิเคราะห์อนุกรมเวลากับปัญหาอื่นๆ เพื่อตัดสินใจว่าเมื่อใดควรให้ยืมเงินแก่กลุ่มผู้กู้ต่างๆ เหล่านี้หรืออัตราการให้กู้ยืม ดอกเบี้ยจะถูกเรียกเก็บจากสมาชิกของกลุ่มพอร์ตโฟลิโอเพื่อชดเชยการขาดทุนระหว่างสมาชิกของกลุ่มนั้น
#3. การวิเคราะห์ความเสี่ยงเชิงสำรวจ
แบบจำลองการคาดการณ์ในธนาคารกำลังได้รับการพัฒนาเพื่อให้เกิดความมั่นใจเกี่ยวกับคะแนนความเสี่ยงสำหรับลูกค้าแต่ละราย คะแนนเครดิตได้รับการออกแบบมาเพื่อทำนายพฤติกรรมที่กระทำผิดของแต่ละบุคคล และมีการใช้กันอย่างแพร่หลายในการประเมินความน่าเชื่อถือทางเครดิตของผู้สมัครแต่ละราย
นอกจากนี้ การวิเคราะห์ความเสี่ยงยังดำเนินการในโลกวิทยาศาสตร์และอุตสาหกรรมประกันภัย นอกจากนี้ยังใช้กันอย่างแพร่หลายในสถาบันการเงิน เช่น บริษัทเกตเวย์การชำระเงินออนไลน์ เพื่อวิเคราะห์ว่าธุรกรรมนั้นเป็นของแท้หรือเป็นการฉ้อโกง
เพื่อจุดประสงค์นี้ พวกเขาใช้ประวัติการทำธุรกรรมของลูกค้า มักใช้ในการซื้อบัตรเครดิต เมื่อมีปริมาณธุรกรรมของลูกค้าเพิ่มขึ้นอย่างกะทันหัน ลูกค้าจะได้รับการโทรยืนยันหากเขาเริ่มธุรกรรม ยังช่วยลดการสูญเสียจากสถานการณ์ดังกล่าว
การวิเคราะห์ข้อมูลเชิงสำรวจด้วย R
สิ่งแรกที่คุณต้องดำเนินการ EDA ด้วย R คือการดาวน์โหลด R base และ R Studio (IDE) ตามด้วยการติดตั้งและโหลดแพ็คเกจต่อไปนี้:
#Installing Packages install.packages("dplyr") install.packages("ggplot2") install.packages("magrittr") install.packages("tsibble") install.packages("forecast") install.packages("skimr") #Loading Packages library(dplyr) library(ggplot2) library(magrittr) library(tsibble) library(forecast) library(skimr)สำหรับบทช่วยสอนนี้ เราจะใช้ชุดข้อมูลเศรษฐศาสตร์ที่มาพร้อมกับ R และให้ข้อมูลตัวบ่งชี้เศรษฐกิจประจำปีของเศรษฐกิจสหรัฐฯ และเปลี่ยนชื่อเป็น econ เพื่อให้เข้าใจง่าย:

econ <- ggplot2::economics 
เพื่อทำการวิเคราะห์เชิงพรรณนา เราจะใช้แพ็คเกจ skimr ซึ่งคำนวณสถิติเหล่านี้ด้วยวิธีที่เรียบง่ายและนำเสนอได้ดี:
#Descriptive Analysis skimr::skim(econ) 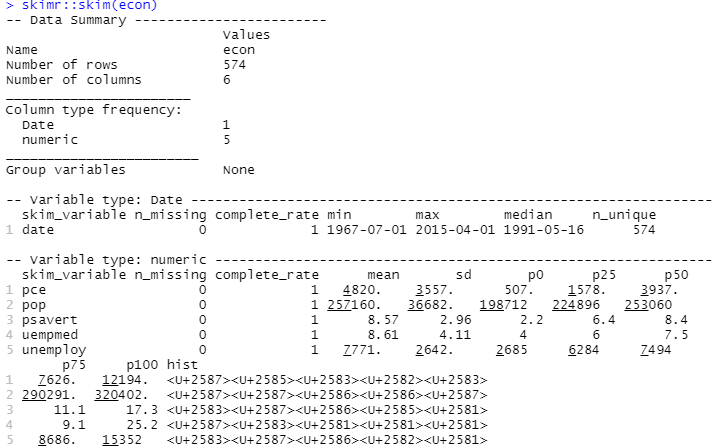
คุณยังสามารถใช้ฟังก์ชัน summary สำหรับการวิเคราะห์เชิงพรรณนา:
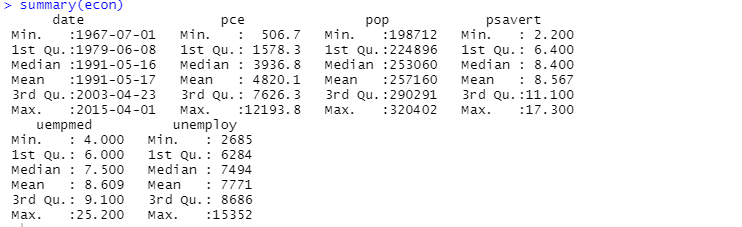
ที่นี่การวิเคราะห์เชิงพรรณนาแสดง 547 แถวและ 6 คอลัมน์ในชุดข้อมูล ค่าต่ำสุดสำหรับ 1967-07-01 และค่าสูงสุดสำหรับ 2015-04-01 นอกจากนี้ยังแสดงค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานอีกด้วย
ตอนนี้คุณมีแนวคิดพื้นฐานแล้วว่ามีอะไรอยู่ในชุดข้อมูล econ เรามาพล็อตฮิสโตแกรมของตัวแปร uempmed เพื่อดูข้อมูลกันดีกว่า:
#Histogram of Unemployment econ %>% ggplot2::ggplot() + ggplot2::aes(x = uempmed) + ggplot2::geom_histogram() + labs(x = "Unemployment", title = "Monthly Unemployment Rate in US between 1967 to 2015") 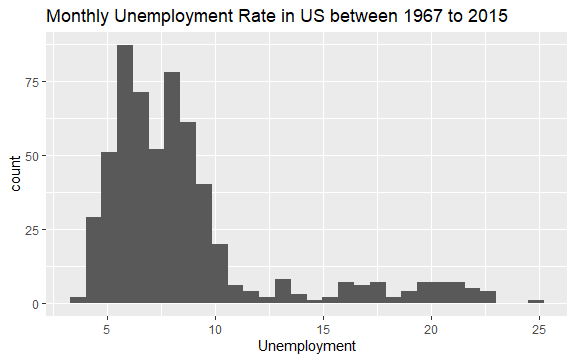
การกระจายของฮิสโตแกรมแสดงให้เห็นว่ามีหางยาวอยู่ทางด้านขวา นั่นคือ อาจมีข้อสังเกตบางประการเกี่ยวกับตัวแปรนี้โดยมีค่า "สุดขั้ว" มากกว่า คำถามเกิดขึ้น: ค่าเหล่านี้เกิดขึ้นในช่วงเวลาใดและแนวโน้มของตัวแปรคืออะไร?
วิธีที่ตรงที่สุดในการระบุแนวโน้มของตัวแปรคือการใช้กราฟเส้น ด้านล่างเราสร้างกราฟเส้นและเพิ่มเส้นเรียบ:
#Line Graph of Unemployment econ %>% ggplot2::autoplot(uempmed) + ggplot2::geom_smooth() 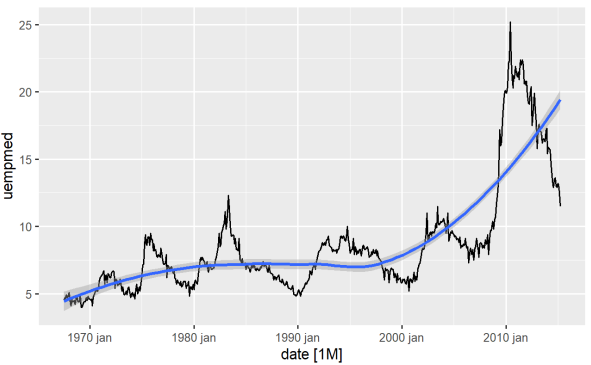
เมื่อใช้กราฟนี้ เราสามารถระบุได้ว่าในช่วงล่าสุด ในการสังเกตครั้งสุดท้ายจากปี 2010 มีแนวโน้มว่าอัตราการว่างงานจะเพิ่มขึ้น เหนือกว่าประวัติศาสตร์ที่สังเกตได้ในทศวรรษที่ผ่านมา
จุดสำคัญอีกจุดหนึ่ง โดยเฉพาะอย่างยิ่งในบริบทการสร้างแบบจำลองทางเศรษฐมิติคือความคงที่ของชุดข้อมูล นั่นคือค่าเฉลี่ยและความแปรปรวนคงที่ตลอดเวลาหรือไม่?
เมื่อสมมติฐานเหล่านี้ไม่เป็นความจริงในตัวแปร เราบอกว่าชุดข้อมูลมีหน่วยรูท (ไม่อยู่กับที่) เพื่อให้การกระแทกที่ตัวแปรได้รับจะสร้างผลกระทบถาวร
ดูเหมือนว่าจะเป็นกรณีของตัวแปรที่เป็นปัญหา ระยะเวลาของการว่างงาน เราได้เห็นแล้วว่าความผันผวนของตัวแปรได้เปลี่ยนแปลงไปอย่างมาก ซึ่งมีนัยสำคัญที่เกี่ยวข้องกับทฤษฎีทางเศรษฐศาสตร์ที่เกี่ยวข้องกับวัฏจักร แต่หากแยกจากทฤษฎี เราจะตรวจสอบได้อย่างไรว่าตัวแปรอยู่กับที่หรือไม่?
แพ็คเกจการคาดการณ์มีฟังก์ชันที่ยอดเยี่ยมทำให้สามารถใช้การทดสอบได้ เช่น ADF, KPSS และอื่นๆ ซึ่งคืนค่าจำนวนความแตกต่างที่จำเป็นสำหรับชุดข้อมูลให้อยู่กับที่แล้ว:
#Using ADF test for checking stationarity forecast::ndiffs( x = econ$uempmed, test = "adf")
ที่นี่ค่า p ที่มากกว่า 0.05 แสดงว่าข้อมูลไม่นิ่ง
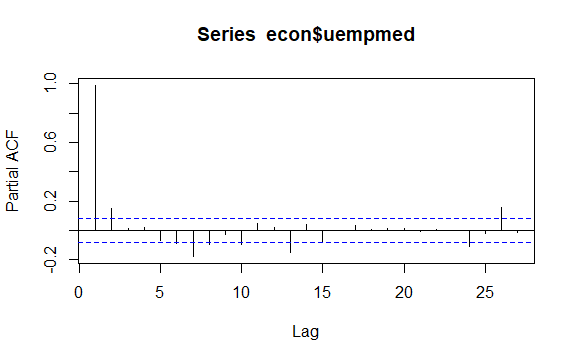
ประเด็นสำคัญอีกประการหนึ่งในอนุกรมเวลาคือการระบุความสัมพันธ์ที่เป็นไปได้ (ความสัมพันธ์เชิงเส้น) ระหว่างค่าที่ล้าหลังของอนุกรม คอร์เรโลแกรมของ ACF และ PACF ช่วยในการระบุ
เนื่องจากชุดข้อมูลไม่มีฤดูกาลแต่มีแนวโน้มที่แน่นอน ความสัมพันธ์อัตโนมัติช่วงแรกมักจะมีขนาดใหญ่และเป็นบวก เพราะการสังเกตการณ์ที่ใกล้เวลานั้นมีค่าใกล้เคียงกัน
ดังนั้น ฟังก์ชันความสัมพันธ์อัตโนมัติ (ACF) ของอนุกรมเวลาที่มีแนวโน้มมักจะมีค่าบวกที่ค่อยๆ ลดลงเมื่อเวลาล่าช้าเพิ่มขึ้น
#Residuals of Unemployment checkresiduals(econ$uempmed) pacf(econ$uempmed) 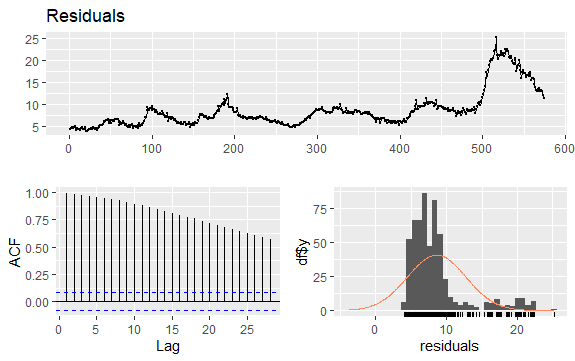
บทสรุป
เมื่อเราได้รับข้อมูลที่สะอาดมากหรือน้อย กล่าวคือ ล้างแล้ว เราถูกล่อลวงให้ดำดิ่งสู่ขั้นตอนการสร้างแบบจำลองทันทีเพื่อวาดผลลัพธ์แรก คุณต้องต่อต้านสิ่งล่อใจนี้และเริ่มทำการวิเคราะห์ข้อมูลเชิงสำรวจ ซึ่งเรียบง่ายแต่ช่วยให้เราดึงข้อมูลเชิงลึกอันทรงพลังเข้าสู่ข้อมูลได้
คุณอาจสำรวจแหล่งข้อมูลที่ดีที่สุดเพื่อเรียนรู้สถิติสำหรับ Data Science
