Rで探索的データ分析(EDA)を行う方法(例付き)
公開: 2022-11-11傾向とパターンを発見し、統計的要約とグラフ表現を利用してデータセットを要約するために使用される重要なプロセスである、探索的データ分析について知っておく必要があるすべてを学びます。
他のプロジェクトと同様に、データ サイエンス プロジェクトは長いプロセスであり、時間、優れた組織、およびいくつかのステップに対する細心の注意が必要です。 探索的データ分析 (EDA) は、このプロセスで最も重要なステップの 1 つです。
したがって、この記事では、探索的データ分析とは何か、R でどのように実行できるかについて簡単に説明します。
探索的データ分析とは
探索的データ分析では、アプリケーションに送信される前に、データセットの特性を調べて調査します。これは、ビジネス、統計、または機械学習に限定されます。

情報の性質とその主な特徴のこの要約は、通常、グラフィック表現や表などの視覚的な方法で行われます。 これらのデータの可能性を正確に評価するために、事前に実践が行われます。これらのデータは、将来、より複雑な処理を受けることになります。
したがって、EDA では次のことが可能です。
- この情報を使用するための仮説を立てます。
- データ構造の隠された詳細を調べます。
- 欠損値、外れ値、または異常な動作を特定します。
- 全体としての傾向と関連する変数を発見します。
- 無関係な変数または他の変数と相関する変数を破棄します。
- 使用するフォーマル モデリングを決定します。
記述的データ分析と探索的データ分析の違いは何ですか?
データ分析には、記述的分析と探索的データ分析の 2 種類があり、目標は異なりますが、密接に関連しています。
1 つ目は、平均、中央値、最頻値などの変数の動作の説明に焦点を当てています。
探索的分析は、変数間の関係を特定し、予備的な洞察を抽出し、モデリングを最も一般的な機械学習パラダイム (分類、回帰、およびクラスタリング) に向けることを目的としています。
共通して、どちらもグラフィック表現を扱うことができます。 ただし、探索的分析のみが実用的な洞察、つまり意思決定者による行動を引き起こす洞察をもたらすことを目指しています。
最後に、探索的データ分析は、問題を解決し、モデル化の手順を導くソリューションを提供しようとしますが、記述的分析は、その名前が示すように、問題のデータセットの詳細な説明を作成することのみを目的としています。
| 記述的分析 | 探索的データ分析 |
| 行動を分析する | 行動と関係を分析する |
| 要約を提供します | 仕様とアクションにつながる |
| 表とグラフでデータを整理します | 表とグラフでデータを整理します |
| 大きな説明力がない | かなりの説明力がある |
EDAの実用的なユースケース
#1。 デジタルマーケティング
デジタル マーケティングは、創造的なプロセスからデータ駆動型のプロセスへと進化しました。 マーケティング組織は、探索的データ分析を使用して、キャンペーンや取り組みの結果を判断し、消費者の投資とターゲティングの決定を導きます。
人口統計調査、顧客セグメンテーション、およびその他の手法により、マーケティング担当者は大量の消費者購入、調査、およびパネル データを使用して、マーケティング戦略を理解し、伝えることができます。
Web 探索的分析により、マーケターは Web サイトでのインタラクションに関するセッション レベルの情報を収集できます。 Google アナリティクスは、マーケティング担当者がこの目的で使用する無料の人気のある分析ツールの一例です。
マーケティングで頻繁に使用される探索的手法には、マーケティング ミックス モデリング、価格設定とプロモーションの分析、販売の最適化、探索的顧客分析 (セグメンテーションなど) が含まれます。
#2。 探索的ポートフォリオ分析
探索的データ分析の一般的なアプリケーションは、探索的ポートフォリオ分析です。 銀行または融資機関には、さまざまな価値とリスクの口座のコレクションがあります。
アカウントは、所有者の社会的地位 (金持ち、中産階級、貧乏人など)、地理的な場所、純資産、およびその他の多くの要因によって異なる場合があります。 貸し手は、ローンの収益と、各ローンのデフォルトのリスクとのバランスを取らなければなりません。 問題は、ポートフォリオ全体をどのように評価するかです。
最もリスクの低いローンは非常に裕福な人向けかもしれませんが、裕福な人の数は非常に限られています。 一方、多くの貧しい人々は貸すことができますが、より大きなリスクがあります。
探索的データ分析ソリューションは、時系列分析を他の多くの問題と組み合わせて、これらの異なる借り手のセグメントにいつお金を貸すか、または貸付率を決定できます。 ポートフォリオ セグメントのメンバー間の損失をカバーするために、ポートフォリオ セグメントのメンバーに利息が課されます。
#3。 探索的リスク分析
銀行の予測モデルは、個々の顧客のリスク スコアについて確実性を提供するために開発されています。 クレジット スコアは、個人の延滞行動を予測するように設計されており、各申請者の信用度を評価するために広く使用されています。
さらに、リスク分析は科学の世界と保険業界で行われています。 また、オンライン決済ゲートウェイ企業などの金融機関でも、トランザクションが本物か不正かを分析するために広く使用されています。
この目的のために、彼らは顧客の取引履歴を使用します。 クレジットカードでの購入でより一般的に使用されます。 クライアントのトランザクション量が急増した場合、クライアントがトランザクションを開始した場合、クライアントは確認の呼び出しを受け取ります。 また、そのような状況による損失を減らすのにも役立ちます。
Rによる探索的データ分析
R で EDA を実行するために最初に必要なことは、R ベースと R Studio (IDE) をダウンロードしてから、次のパッケージをインストールしてロードすることです。
#Installing Packages install.packages("dplyr") install.packages("ggplot2") install.packages("magrittr") install.packages("tsibble") install.packages("forecast") install.packages("skimr") #Loading Packages library(dplyr) library(ggplot2) library(magrittr) library(tsibble) library(forecast) library(skimr)このチュートリアルでは、R に組み込まれており、米国経済の年間経済指標データを提供する経済学データセットを使用し、簡単にするためにその名前を econ に変更します。
econ <- ggplot2::economics 
記述的分析を実行するために、 skimrパッケージを使用します。これは、これらの統計をシンプルかつ適切に提示された方法で計算します。

#Descriptive Analysis skimr::skim(econ) 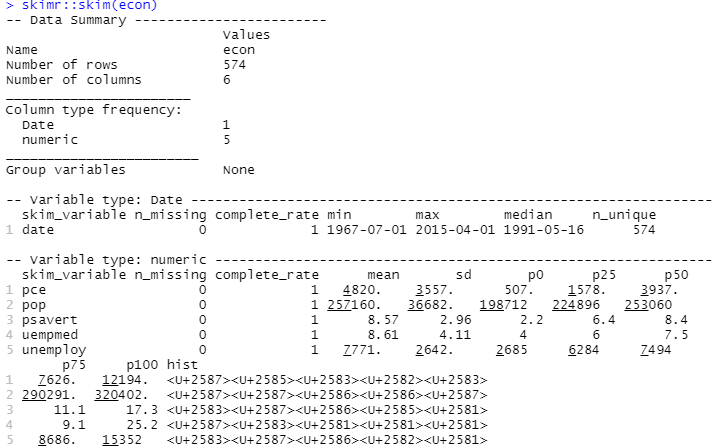
記述的分析には、 summary関数を使用することもできます。
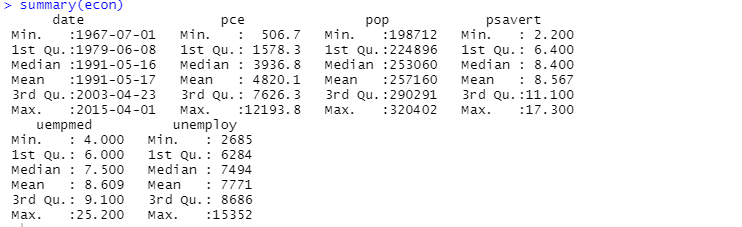
ここで、記述的分析は、データセット内の 547 行と 6 列を示しています。 最小値は 1967 年 7 月 1 日、最大値は 2015 年 4 月 1 日です。 同様に、平均値と標準偏差も表示されます。
これで、経済データセットの内容に関する基本的なアイデアが得られました。 データをよく見るために、変数uempmedのヒストグラムをプロットしてみましょう。
#Histogram of Unemployment econ %>% ggplot2::ggplot() + ggplot2::aes(x = uempmed) + ggplot2::geom_histogram() + labs(x = "Unemployment", title = "Monthly Unemployment Rate in US between 1967 to 2015") 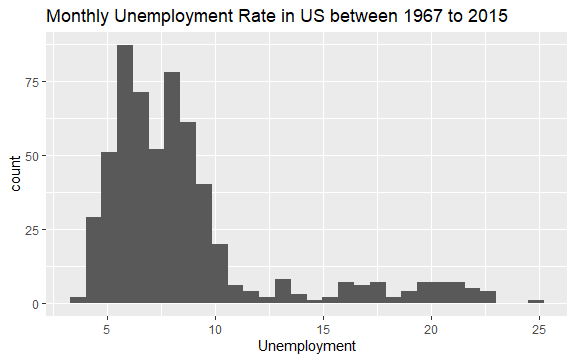
ヒストグラムの分布は、右側に細長いテールがあることを示しています。 つまり、より「極端な」値を持つこの変数の観測がいくつかある可能性があります。 問題が発生します。これらの値が発生したのはどの時期で、変数の傾向は何ですか?
変数の傾向を識別する最も直接的な方法は、折れ線グラフを使用することです。 以下では、折れ線グラフを生成し、平滑化線を追加します。
#Line Graph of Unemployment econ %>% ggplot2::autoplot(uempmed) + ggplot2::geom_smooth() 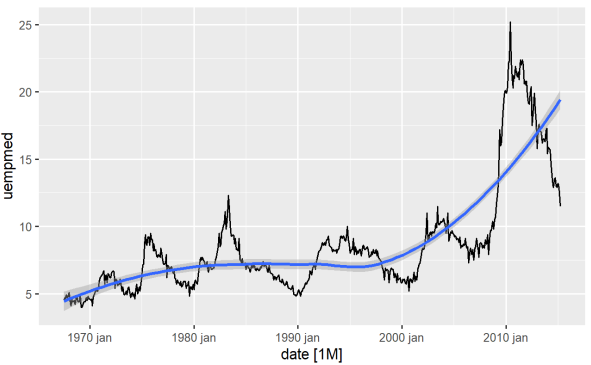
このグラフを使用すると、最近の期間、2010 年からの最後の観測では、失業率が増加する傾向があり、過去数十年間に観測された履歴を上回っていることがわかります。
もう 1 つの重要なポイントは、特に計量経済モデリングのコンテキストで、系列の定常性です。 つまり、平均と分散は時間の経過とともに一定ですか?
これらの仮定が変数に当てはまらない場合、変数が受けるショックが永続的な効果を生み出すように、系列に単位根 (非定常) があると言えます。
問題の変数である失業期間の場合はそうであったようです。 変数の変動が大幅に変化したことがわかりました。これは、サイクルを扱う経済理論に関連する強い意味を持っています。 しかし、理論から離れて、変数が静止しているかどうかを実際に確認するにはどうすればよいでしょうか?
予測パッケージには、ADF、KPSS などのテストを適用できる優れた機能があり、系列が定常であるために必要な差の数を既に返しています。
#Using ADF test for checking stationarity forecast::ndiffs( x = econ$uempmed, test = "adf")
ここで、0.05 より大きい p 値は、データが非定常であることを示しています。
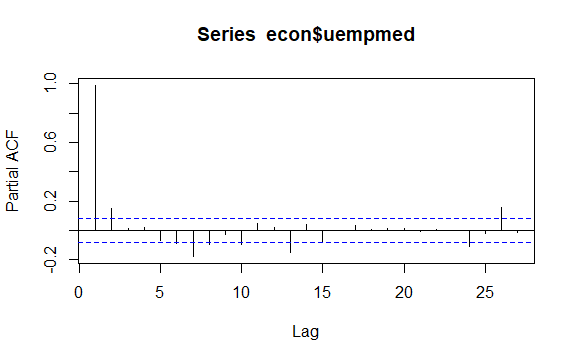
時系列のもう 1 つの重要な問題は、系列のラグ値間の可能な相関関係 (線形関係) の識別です。 ACF および PACF コレログラムは、それを識別するのに役立ちます。
シリーズには季節性はありませんが、特定の傾向があるため、時間的に近い観測値も近いため、初期の自己相関は大きく正になる傾向があります。
したがって、傾向のある時系列の自己相関関数 (ACF) は、ラグが増加するにつれてゆっくりと減少する正の値を持つ傾向があります。
#Residuals of Unemployment checkresiduals(econ$uempmed) pacf(econ$uempmed) 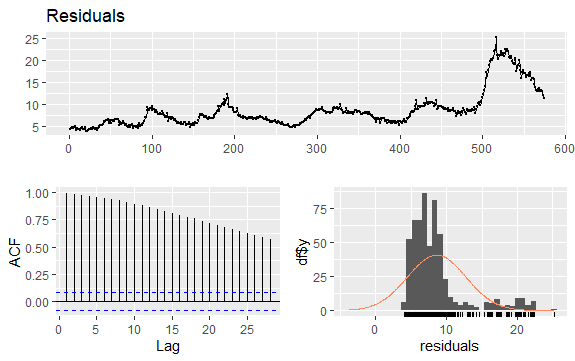
結論
多かれ少なかれクリーンなデータ、つまり既にクリーンアップされたデータを手に入れると、すぐにモデル構築段階に飛び込んで最初の結果を導き出そうとします。 この誘惑に抵抗し、探索的データ分析を開始する必要があります。これは単純ですが、データに強力な洞察を引き出すのに役立ちます。
また、データ サイエンスの統計を学習するための最適なリソースを探すこともできます。
