NumPy linspace(): как создавать массивы равномерно расположенных чисел
Опубликовано: 2022-04-11В этом руководстве вы узнаете, как использовать NumPy linspace() для создания массива равномерно расположенных чисел в Python.
Вы изучите синтаксис NumPy linspace() , а затем примеры, которые помогут вам понять, как его использовать.
Примечание. Чтобы следовать этому руководству, вам необходимо установить Python и NumPy.
У вас еще нет NumPy? Мы составили для вас краткое руководство по установке.
Давайте начнем!
Установите и импортируйте NumPy
Прежде чем приступить к руководству, давайте быстро выполним шаги по установке библиотеки NumPy.
Если у вас уже установлен NumPy, смело переходите к следующему разделу.
- Если вы используете Google Colab — облачную среду для ноутбуков Jupyter, вы можете импортировать NumPy и сразу приступить к программированию. (рекомендуется для этого урока)
- Если вы хотите настроить локальную рабочую среду, я рекомендую установить дистрибутив Python Anaconda. Anaconda поставляется с несколькими предустановленными полезными пакетами. Вы можете скачать установщик для своей операционной системы. Процесс настройки занимает всего несколько минут.
- Если на вашем компьютере уже установлен Python, вы все равно можете установить дистрибутив Anaconda. Вы можете использовать conda или pip для установки пакетов и управления ими. Вы можете запустить одну из следующих команд из командной строки Anaconda, чтобы установить NumPy.
# Install NumPy using conda conda install numpy # Install NumPy using pip pip install numpy В качестве следующего шага импортируйте numpy под псевдонимом np , выполнив следующую команду. Это поможет вам ссылаться на NumPy как на np — без необходимости вводить numpy каждый раз, когда вы обращаетесь к элементу в модуле.
import numpy as np В дальнейшем мы будем использовать запись через точку для доступа ко всем функциям в библиотеке NumPy следующим образом: np.<func-name> .
Дело о равномерно распределенных числах
Когда вы работаете с массивами NumPy, бывают случаи, когда вам нужно создать массив равномерно расположенных чисел в интервале.
Прежде чем идти дальше, давайте быстро рассмотрим другую похожую функцию np.arange() .
NumPy linspace() против NumPy arange()
Если вы использовали NumPy раньше, вы, вероятно, использовали np.arange() для создания массива чисел в указанном диапазоне.
Вы знаете, что
np.arange(start, stop, step)возвращает массив чисел отstartдо, но не включаяstop, в шагахstep; размер шага по умолчанию равен 1.
Однако значение шага не всегда может быть очевидным. Давайте посмотрим, почему это так.
Например, если вам нужно 4 равномерно расположенных числа от 0 до 1, вы знаете, что размер шага должен быть 0,25. Но если вы используете np.arange() , он не включает стоп-значение 1. Поэтому вам придется выбрать интервал, выходящий за стоп-значение.
Следующее изображение иллюстрирует еще несколько примеров, где вам нужно определенное количество равномерно расположенных точек в интервале [a, b].
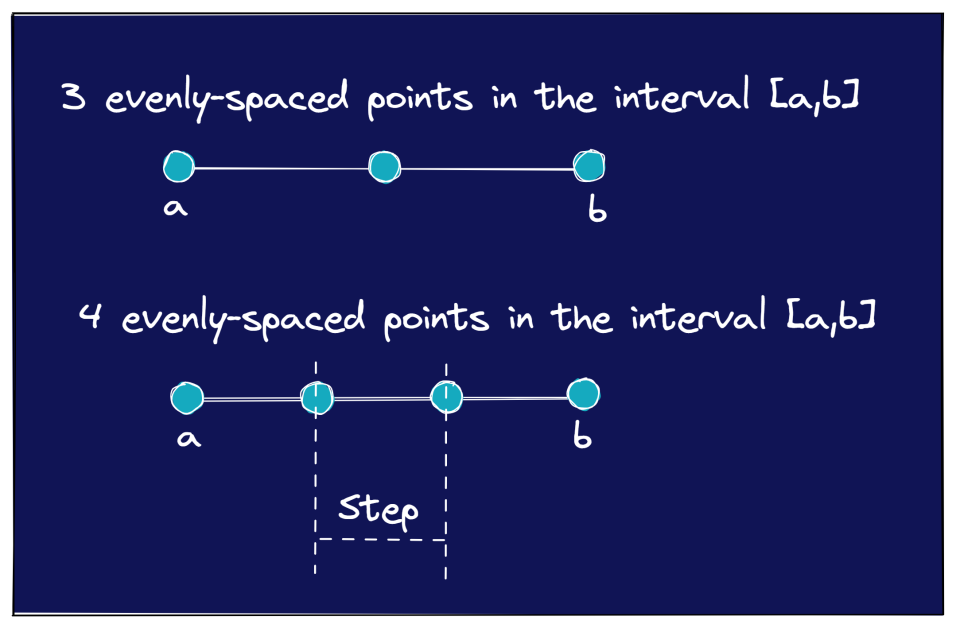
Наш первый пример с 4 равномерно расположенными точками в [0,1] был достаточно простым. Вы знаете, что размер шага между точками должен быть 0,25.
Предположим, у вас есть немного более сложный пример, в котором вам нужно перечислить 7 равномерно расположенных точек от 1 до 33. Здесь размер шага может быть не очень ясен сразу. Однако в этом случае вы можете вручную определить значение step .
Однако np.linspace() сделать это еще проще!

При использовании np.linspace() вам нужно указать только количество точек в интервале, не беспокоясь о размере шага. И вы вернете массив по желанию.
С этой мотивацией давайте приступим к изучению синтаксиса NumPy linspace() в следующем разделе.
Синтаксис NumPy linspace()
Синтаксис использования NumPy linspace() показан ниже:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)На первый взгляд приведенный выше синтаксис может показаться очень сложным с множеством параметров.
Однако большинство из них являются необязательными параметрами, и мы получим гораздо более простой синтаксис всего за пару минут.
Теперь давайте начнем с разбора приведенного выше синтаксиса:
-
startиstop— начальная и конечная точки интервала соответственно. И start, и stop могут быть скалярами или массивами. В этом руководстве мы ограничимся скалярными начальными и конечными значениями. -
num— количество равномерно расположенных точек. И это необязательный параметр со значением по умолчанию 50. -
endpointтакже является необязательным параметром, который может принимать значения True или False. - Значение по умолчанию — True, что означает, что конечная точка будет включена в интервал по умолчанию. Однако вы можете установить значение False, чтобы исключить конечную точку.
-
retstep— еще один необязательный параметр, который принимает логические значения True или False. Если установлено значение True, возвращается значение шага. -
dtype— это тип данных чисел в массиве. Тип обычно подразумевается как float и не требует явного указания. -
axis— еще один необязательный параметр, обозначающий ось, вдоль которой должны храниться числа. И это актуально только тогда, когдаstartиstopзначения сами являются массивами.
️ Так что же np.linspace() ?
Он возвращает N-мерный массив равномерно расположенных чисел. И если для параметра retstep установлено значение True , он также возвращает размер шага.
Основываясь на обсуждении, вот упрощенный синтаксис для использования np.linspace() :
np.linspace(start, stop, num)Вышеупомянутая строка кода вернет массив
numравномерно расположенных чисел в интервале[start, stop].
Теперь, когда вы знаете синтаксис, давайте начнем кодировать примеры.
Как создать равномерно распределенные массивы с помощью NumPy linspace()
№1. В качестве первого примера создадим массив из 20 равномерно расположенных чисел в интервале [1, 5].

Вы можете указать значения start , stop и num в качестве аргументов ключевого слова. Это показано в ячейке кода ниже:
import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] Обратите внимание, что числа в массиве начинаются с 1 и заканчиваются на 5, включая обе конечные точки. Кроме того, обратите внимание, как числа, включая точки 1 и 5, представлены как числа с float в возвращаемом массиве.
№ 2. В предыдущем примере вы передали значения start , stop и num в качестве аргументов ключевого слова . Если вы передаете аргументы в правильном порядке, вы можете также использовать их как позиционные аргументы только со значениями, как показано ниже.
import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] №3. Теперь давайте создадим еще один массив, в котором мы установим retstep в True .
Это означает, что теперь функция будет возвращать и массив, и шаг. И мы можем распаковать их в две переменные arr3 : массив и step_size : возвращаемый размер шага.
Следующая ячейка кода объясняет, как вы можете это сделать.
import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # Output: print(step_size) 0.21052631578947367 № 4. В качестве последнего примера давайте установим endpoint в False и проверим, что произойдет.
import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # Output: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]В возвращенном массиве вы можете видеть, что 1 включено, а 5 не включено. И последнее значение в массиве равно 4,8, но у нас все еще есть 20 чисел.
До сих пор мы генерировали только массивы равномерно расположенных чисел. В следующем разделе давайте визуализируем, нанося эти числа на график.
Как построить равномерно распределенные числа в интервале
В этом разделе давайте выберем [10,15] в качестве интересующего нас интервала. А затем используйте np.linspace() для создания двух массивов, каждый из которых имеет 8 и 12 точек соответственно.
После того, как это будет завершено, мы можем использовать функцию построения графика из библиотеки matplotlib для их построения.
Для ясности мы зафиксируем два массива из N1 = 8 и N2 = 12 равномерно расположенных точек в разных положениях вдоль оси Y.
Следующий фрагмент кода демонстрирует это.
import numpy as np import matplotlib.pyplot as plt N1 = 8 N2 = 12 a = 10 b = 15 y1 = np.zeros(N1) y2 = np.zeros(N2) x1 = np.linspace(a, b, N1) x2 = np.linspace(a, b, N2) plt.plot(x1, y1-0.5, 'o') plt.plot(x2, y2 + 0.5, 'o') plt.ylim([-1, 1]) plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]') plt.xlabel('Interval') plt.show() 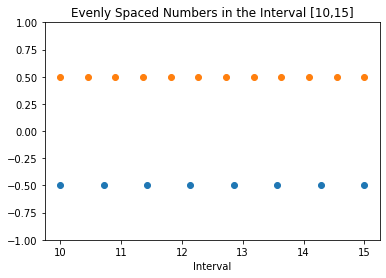
Генерация равномерно расположенных точек может быть полезна при работе с математическими функциями. Мы узнаем об этом в следующем разделе.
Как использовать NumPy linspace() с математическими функциями
После того, как вы сгенерировали массив равномерно распределенных чисел с помощью np.linspace() , вы можете вычислить значения математических функций в интервале.
В кодовой ячейке ниже вы сначала создаете 50 равномерно расположенных точек в интервале от 0 до 2π. А затем создайте массив y с помощью np.sin() в массиве x . Обратите внимание, что вы можете пропустить параметр num , так как значение по умолчанию равно 50. Мы по-прежнему будем использовать его явно.
В качестве следующего шага вы можете построить синусоидальную функцию в интервале [0, 2π]. Для этого можно использовать matplotlib, как и в предыдущем примере. В частности, функция plot() в matplotlib.pytplot используется для создания линейного графика.
import numpy as np import matplotlib.pyplot as plt N = 50 a = 0.0 b = 2*np.pi x = np.linspace(a, b, N) y = np.sin(x) plt.plot(x, y, marker = "o") plt.ylim([-1, 1]) plt.title(f'y = sin(x)') plt.xlabel('x ---->') plt.show() 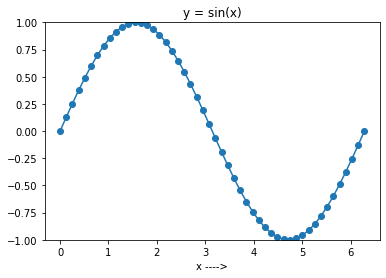
Теперь запустите приведенный выше код, установив N равным 10. Вы получите график, как показано на рисунке ниже.
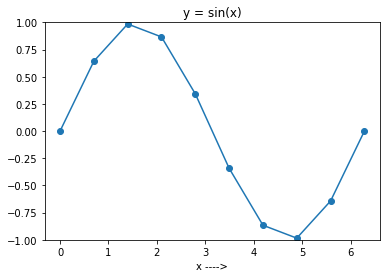
И вы можете видеть, что график не очень гладкий, так как вы выбрали только 10 точек в интервале.
Как правило, чем большее количество точек вы рассматриваете, тем более плавным будет график функции.
Вывод
Вот краткое изложение того, что мы узнали.
- np.linspace(start, stop, num) возвращает массив из num равномерно расположенных чисел в интервале [start, stop] .
- Установите конечную точку необязательного параметра на False , чтобы исключить stop , и установите интервал на [start, stop) .
- При необходимости установите для параметра retstep значение True , чтобы получить размер шага.
- Создавайте равномерно распределенные массивы с помощью np.linspace() , а затем используйте массив с математическими функциями.
Надеюсь, теперь вы понимаете, как работает np.linspace() . Вы можете запустить приведенные выше примеры в блокноте Jupyter. Ознакомьтесь с нашим руководством по ноутбуку Jupyter или другим альтернативам Jupyter, которые вы можете рассмотреть.
До скорой встречи в другом учебнике по Python. А пока продолжайте кодить!
