NumPy linspace (): كيفية إنشاء مصفوفات من أرقام متباعدة بشكل متساوٍ

سيعلمك هذا البرنامج التعليمي كيفية استخدام NumPy linspace () لإنشاء مصفوفة من الأرقام المتباعدة بشكل متساوٍ في بايثون.

ستتعلم صيغة linspace() ، متبوعة بأمثلة ستساعدك على فهم كيفية استخدامها.

ملاحظة: لمتابعة هذا البرنامج التعليمي ، تحتاج إلى تثبيت Python و NumPy.

ليس لديك NumPy حتى الآن؟ لقد قمنا بتجميع دليل التثبيت السريع من أجلك.

لنبدأ!

تثبيت واستيراد NumPy

قبل بدء البرنامج التعليمي ، دعنا ننتقل بسرعة من خلال الخطوات لتثبيت مكتبة NumPy.

إذا كان لديك NumPy مثبتًا بالفعل ، فلا تتردد في التخطي إلى القسم التالي.

• إذا كنت تستخدم Google Colab — بيئة دفتر ملاحظات Jupyter المستندة إلى مجموعة النظراء ، يمكنك استيراد NumPy وبدء الترميز على الفور. (موصى به لهذا البرنامج التعليمي)
• إذا كنت ترغب في إعداد بيئة عمل محلية ، فإنني أوصي بتثبيت توزيعة Anaconda من Python. Anaconda يأتي مع العديد من الحزم المفيدة المثبتة مسبقًا. يمكنك تنزيل المثبت لنظام التشغيل الخاص بك. تستغرق عملية الإعداد بضع دقائق فقط.
• إذا كان لديك Python مثبتًا بالفعل على جهاز الكمبيوتر الخاص بك ، فلا يزال بإمكانك تثبيت توزيع Anaconda. يمكنك استخدام conda أو pip لتثبيت وإدارة الحزم. يمكنك تشغيل أحد الأوامر التالية من موجه أوامر Anaconda لتثبيت NumPy.

 # Install NumPy using conda conda install numpy # Install NumPy using pip pip install numpy

كخطوة تالية ، قم باستيراد numpy تحت الاسم المستعار np عن طريق تشغيل الأمر التالي. سيساعدك القيام بذلك على الإشارة إلى NumPy كـ np - دون الحاجة إلى كتابة numpy في كل مرة تقوم فيها بالوصول إلى عنصر في الوحدة النمطية.

 import numpy as np

من الآن فصاعدًا ، سنستخدم تدوين النقطة للوصول إلى جميع الوظائف في مكتبة NumPy مثل هذا: np.<func-name> .

الحال بالنسبة للأرقام المتباعدة بشكل متساوٍ

عندما تعمل باستخدام مصفوفات NumPy ، هناك أوقات ستحتاج فيها إلى إنشاء مصفوفة من الأرقام المتباعدة بشكل متساوٍ في فاصل زمني.

قبل أن نذهب إلى أبعد من ذلك ، دعنا ننتقل بسرعة إلى وظيفة أخرى مماثلة np.arange() .

NumPy linspace () مقابل NumPy arange ()

إذا كنت قد استخدمت NumPy من قبل ، فمن المحتمل أنك استخدمت np.arange() لإنشاء مصفوفة من الأرقام ضمن نطاق محدد.

أنت تعلم أن np.arange(start, stop, step) ترجع مصفوفة من الأرقام من start إلى لكن لا تشمل stop ، في خطوات step ؛ حجم الخطوة الافتراضي هو 1.

ومع ذلك ، قد لا تكون قيمة الخطوة واضحة دائمًا. دعونا نرى لماذا هذا هو الحال.

على سبيل المثال ، إذا كنت بحاجة إلى 4 أرقام متباعدة بشكل متساوٍ بين 0 و 1 ، فأنت تعلم أن حجم الخطوة يجب أن يكون 0.25. ولكن إذا كنت تستخدم np.arange() ، فإنها لا تتضمن قيمة الإيقاف 1. لذا سيتعين عليك اختيار فترة تتجاوز قيمة الإيقاف.

توضح الصورة التالية بعض الأمثلة الأخرى حيث تحتاج إلى عدد محدد من النقاط المتباعدة بشكل متساوٍ في الفاصل الزمني [أ ، ب].

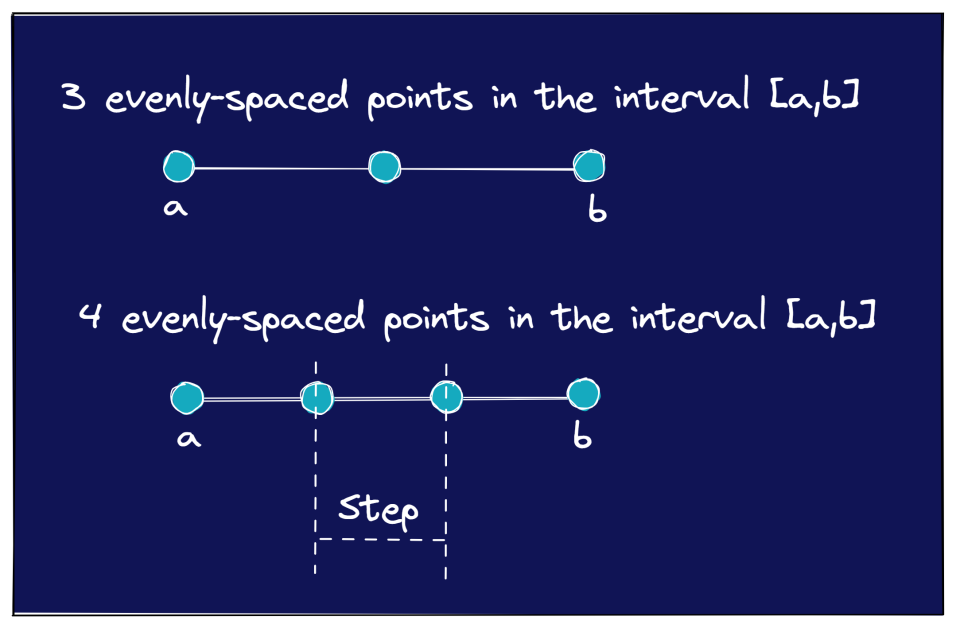
كان مثالنا الأول المكون من 4 نقاط متباعدة بشكل متساوٍ في [0،1] سهلاً بدرجة كافية. أنت تعلم أن حجم الخطوة بين النقاط يجب أن يكون 0.25.

افترض أن لديك مثالًا أكثر ارتباطًا بقليل - حيث كان عليك سرد 7 نقاط متباعدة بشكل متساوٍ بين 1 و 33. هنا ، قد لا يكون حجم الخطوة واضحًا جدًا على الفور. ومع ذلك ، يمكنك تحديد قيمة step يدويًا في هذه الحالة.

ومع ذلك ، فإن np.linspace() موجود هنا لجعله أكثر بساطة بالنسبة لك!

عند استخدام np.linspace() ، ما عليك سوى تحديد عدد النقاط في الفاصل الزمني — دون القلق بشأن حجم الخطوة. وستستعيد المصفوفة حسب الرغبة.

مع هذا الدافع ، دعنا ننتقل إلى تعلم بناء جملة linspace() في القسم التالي.

بناء جملة NumPy linspace ()

يتم عرض بناء جملة استخدام linspace() أدناه:

 np.linspace(start, stop, num, endpoint, retstep, dtype, axis)

في البداية ، قد يبدو بناء الجملة أعلاه معقدًا للغاية مع العديد من المعلمات.

ومع ذلك ، فإن معظمها عبارة عن معلمات اختيارية ، وسنصل إلى صياغة أبسط بكثير في غضون دقيقتين فقط.

لنبدأ الآن بتحليل الصيغة أعلاه:

• start stop هما نقطتا البداية والنهاية للفاصل الزمني ، على التوالي. يمكن أن يكون كل من start و stop حجميًا أو مصفوفات. سنقتصر على قيم البداية والنهاية العددية في هذا البرنامج التعليمي.
• num هو عدد النقاط المتباعدة بشكل متساوٍ. وهي معلمة اختيارية بقيمة افتراضية 50.
• endpoint هي أيضًا معلمة اختيارية يمكن أن تكون إما صواب أو خطأ.
• القيمة الافتراضية هي True ، مما يعني أنه سيتم تضمين نقطة النهاية في الفاصل الزمني افتراضيًا. ومع ذلك ، يمكنك تعيينه على False لاستبعاد نقطة النهاية.
• retstep هي معلمة اختيارية أخرى تأخذ Booleans True أو False. عند التعيين على True ، يتم إرجاع قيمة الخطوة.
• dtype هو نوع بيانات الأرقام في المصفوفة. عادةً ما يُستدل على النوع على أنه عائم ولا يلزم تقديمه صراحةً.
• axis هو معلمة اختيارية أخرى تشير إلى المحور الذي يجب تخزين الأرقام على طوله. وهذا مهم فقط عندما تكون قيم start والنهاية عبارة stop مصفوفتين بحد ذاتها.

️ إذن ما الذي np.linspace() ؟

تقوم بإرجاع مصفوفة ذات أبعاد N من أرقام متباعدة بشكل متساوٍ. وإذا تم ضبط المعلمة retstep على True ، فإنها تُرجع أيضًا حجم الخطوة.

بناءً على المناقشة حتى الآن ، إليك صيغة مبسطة لاستخدام np.linspace() :

 np.linspace(start, stop, num)

سيعود سطر التعليمات البرمجية أعلاه مصفوفة من الأرقام num بشكل متساوٍ في الفاصل الزمني [start, stop] .

الآن بعد أن تعرفت على النحو ، فلنبدأ في أمثلة الترميز.

كيفية إنشاء مصفوفات متباعدة بشكل متساوٍ باستخدام NumPy linspace ()

# 1. كمثالنا الأول ، لنقم بإنشاء مصفوفة من 20 رقمًا متباعدة بشكل متساوٍ في الفترة [1 ، 5].

يمكنك تحديد قيم start و stop و num أساسية. هذا موضح في خلية الكود أدناه:

 import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]

لاحظ كيف تبدأ الأرقام في المصفوفة عند 1 وتنتهي عند 5 - بما في ذلك نقطتا النهاية. لاحظ أيضًا كيف يتم تمثيل الأرقام ، بما في ذلك النقطتان 1 و 5 على أنها float في المصفوفة التي تم إرجاعها.

# 2. في المثال السابق ، مررت قيم start و stop و num أساسية . إذا قمت بتمرير الوسيطات بالترتيب الصحيح ، فيمكنك أيضًا استخدامها كوسيطات موضعية مع القيم فقط ، كما هو موضح أدناه.

 import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]

# 3. لنقم الآن بإنشاء مصفوفة أخرى حيث قمنا بتعيينها retstep إلى True .

هذا يعني أن الوظيفة ستعيد الآن كلاً من المصفوفة والخطوة. ويمكننا فك حزمهم إلى متغيرين arr3 : المصفوفة و step_size : حجم الخطوة المُعادة.

تشرح خلية الكود التالية كيف يمكنك القيام بذلك.

 import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # Output: print(step_size) 0.21052631578947367

# 4. كمثال أخير ، دعنا نضع endpoint على False ، ونتحقق مما يحدث.

 import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # Output: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]

في المصفوفة التي تم إرجاعها ، يمكنك أن ترى أن 1 مضمن ، في حين لم يتم تضمين 5. والقيمة الأخيرة في المصفوفة هي 4.8 ، لكن لا يزال لدينا 20 رقمًا.

حتى الآن ، قمنا فقط بإنشاء مصفوفات من الأرقام المتباعدة بشكل متساوٍ. في القسم التالي ، دعنا نتخيل من خلال رسم هذه الأرقام.

كيفية رسم أرقام متباعدة بشكل متساوٍ في فترة زمنية

في هذا القسم ، دعنا نختار [10 ، 15] على أنها الفترة الزمنية التي تهمنا. ثم استخدم np.linspace() لتوليد مصفوفتين ، كل منهما 8 و 12 نقطة ، على التوالي.

بعد اكتمال ذلك ، يمكننا استخدام وظيفة الرسم من مكتبة matplotlib .

من أجل الوضوح ، سنثبت مصفوفتي N1 = 8 و N2 = 12 نقطة متباعدة بشكل متساوٍ في مواضع مختلفة على طول المحور y.

يوضح مقتطف الشفرة التالي هذا.

 import numpy as np import matplotlib.pyplot as plt N1 = 8 N2 = 12 a = 10 b = 15 y1 = np.zeros(N1) y2 = np.zeros(N2) x1 = np.linspace(a, b, N1) x2 = np.linspace(a, b, N2) plt.plot(x1, y1-0.5, 'o') plt.plot(x2, y2 + 0.5, 'o') plt.ylim([-1, 1]) plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]') plt.xlabel('Interval') plt.show()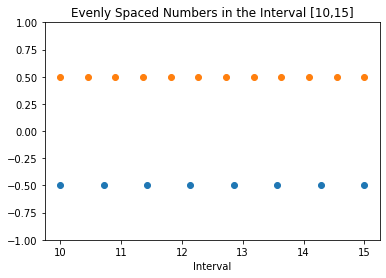

يمكن أن يكون إنشاء نقاط متباعدة بشكل متساوٍ مفيدًا عند التعامل مع الدوال الرياضية. سنتعرف على ذلك في القسم التالي.

كيفية استخدام NumPy linspace () مع وظائف الرياضيات

بعد إنشاء مصفوفة من الأرقام المتباعدة بشكل متساوٍ باستخدام np.linspace() ، يمكنك حساب قيم الدوال الرياضية في الفاصل الزمني.

في خلية الشفرة أدناه ، تقوم أولاً بإنشاء 50 نقطة متباعدة بشكل متساوٍ في الفاصل الزمني من 0 إلى 2 درجة. ثم أنشئ المصفوفة y باستخدام np.sin() في المصفوفة x . لاحظ أنه يمكنك تخطي المعلمة num ، حيث إن القيمة الافتراضية هي 50. سنستمر في استخدامها بشكل صريح.

كخطوة تالية ، يمكنك رسم دالة الجيب في الفترة [0 ، 2π]. للقيام بذلك ، يمكنك استخدام matplotlib ، كما في المثال السابق. على وجه التحديد ، تُستخدم الدالة plot() في matplotlib.pytplot لإنشاء مخطط خطي.

 import numpy as np import matplotlib.pyplot as plt N = 50 a = 0.0 b = 2*np.pi x = np.linspace(a, b, N) y = np.sin(x) plt.plot(x, y, marker = "o") plt.ylim([-1, 1]) plt.title(f'y = sin(x)') plt.xlabel('x ---->') plt.show()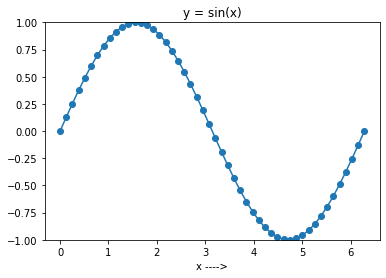

الآن ، قم بتشغيل الكود أعلاه عن طريق تعيين N يساوي 10. ستحصل على المؤامرة كما هو موضح في الشكل أدناه.

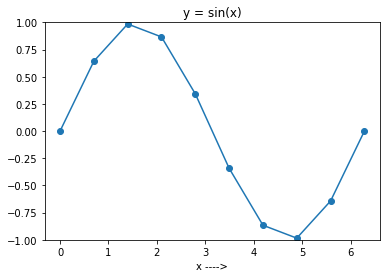
ويمكنك أن ترى أن الحبكة ليست سلسة للغاية — حيث أنك اخترت 10 نقاط فقط في الفترة الزمنية.

بشكل عام ، كلما زاد عدد النقاط التي تضعها في الاعتبار ، سيكون مخطط الوظيفة أكثر سلاسة.

استنتاج

هذا ملخص لما تعلمناه.

• يقوم np.linspace (بدء ، إيقاف ، عدد) بإرجاع مصفوفة من الأرقام المتباعدة بشكل متساوٍ في الفاصل الزمني [بدء ، إيقاف] .
• اضبط نقطة نهاية المعلمة الاختيارية على False لاستبعاد التوقف ، واضبط الفاصل الزمني على [بدء ، إيقاف) .
• اضبط retstep على True اختياريًا للحصول على حجم الخطوة.
• أنشئ مصفوفات متباعدة بشكل متساوٍ باستخدام np.linspace () ، ثم استخدم المصفوفة مع الدوال الرياضية.

أتمنى أن تفهم الآن كيف يعمل np.linspace () . يمكنك اختيار تشغيل الأمثلة المذكورة أعلاه في دفتر Jupyter. تحقق من دليلنا على دفتر Jupyter أو بدائل Jupyter الأخرى التي يمكنك وضعها في الاعتبار.

نراكم جميعًا قريبًا في برنامج تعليمي بيثون آخر. حتى ذلك الحين ، استمر في البرمجة!